2023-2024学年湘教版初中数学七年级下册 1.4 三元一次方程组同步分层训练培优题

试卷更新日期：2024-01-26 类型：同步测试

进入出卷网下载

一、选择题

1. 若 ${\begin{cases} x = 3 - m \\ y = 1 + 2 m \end{cases}$ ，则y用含x的代数式表示为（）

A、 $y = 2 x + 7$ B、 $y = - 2 x + 7$ C、 $y = 2 x - 5$ D、 $y = - 2 x - 5$

查看试题解析
2. 若 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 7 \\ \frac{1}{2} b x + 2 c y = 5 \end{array}$ 的解，则 $a - c$ 的值是（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
3. 《孙子算经》中有一个问题：今有甲、乙、丙三人持钱 .甲语乙、丙：“各将公等所持钱半以益我，钱成九十 .”乙复语甲、丙：“各将公等所持钱半以益我，钱成七十 .”丙复语甲、乙：“各将公等所持钱半以益我，钱成五十六 .”若设甲、乙各持钱数为x、y，则丙持钱数不可以表示为（）

A、 $56 - \frac{x}{2} - \frac{y}{2}$ B、 $180 - 2 x - y$ C、 $140 - 2 x - y$ D、 $140 - x - 2 y$

查看试题解析
4. 已知a-b＝2，a-c＝ $\frac{1}{2}$ ，则代数式（b-c）²+3（b-c）+ $\frac{9}{4}$ 的值是（）

A、- $\frac{3}{2}$ B、 $\frac{3}{2}$ C、0 D、 $\frac{9}{4}$

查看试题解析
5. 如图，三个天平的托盘中形状相同的物体质量相等．图①、图②所示的两个天平处于平衡状态，要使第三个天平也保持平衡，可在它的右盘中放置（）

A、3个球 B、4个球 C、5个球 D、6个球

查看试题解析
6. 对于代数式ax²﹣2bx﹣c，当x取﹣1时，代数式的值为2，当x取0时，代数式的值为1，当x取3时，代数式的值为2，则当x取2时，代数式的值是（）

A、1 B、3 C、4 D、5

查看试题解析
7. 若二元一次方程3x﹣y=7，2x+3y=1，y=kx﹣9有公共解，则k的取值为（）

A、3 B、﹣3 C、﹣4 D、4

查看试题解析
8. 利用两块相同的长方体木块测量一张桌子的高度．首先按图①方式放置，再交换两木块的位置，按图②方式放置．测量的数据如图，则桌子的高度是（）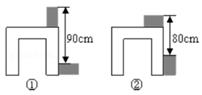

A、84cm B、85cm C、86cm D、87cm

查看试题解析

二、填空题

9. 三元一次方程组 ${\begin{array}{l} x + y = 1 \\ y + z = 2 \\ x + z = 3 \end{array}$ 的解是.

查看试题解析
10. 已知a，b，c为三个非负实数，且满足 ${\begin{array}{l} a + b + c = 30 \\ 2 a + 3 b + 4 c = 100 \end{array}$ ，若 $W = 3 a + 2 b + 5 c$ ，则W的最大值为.

查看试题解析
11. 冰墩墩和雪容融到校门外文具店买文件，冰墩墩购铅笔2支，练习本2本，圆珠笔1支，共付9元钱；雪容融购同样铅笔1支，练习本4本，圆珠笔2支，共付12元钱，若小明去购买与她们一样的铅笔1支、练习本2本、圆珠笔1支，他需付元钱.

查看试题解析
12. 某小区为了优化环境，计划在小区内甲、乙两块面积相同的空地上种植矮牵牛、金盏菊和三色堇三种花卉.现有10名工人参与种植，且每名工人每天种植矮牵牛、金盏菊和三色堇的面积之比为 $5 ： 4 ： 2$ .已知每名工人固定种植一种花卉，所有工人花费9天的时间完成了甲地的花卉种植.在乙地进行花卉种植时，为了加快乙地的种植进度，基于甲地的工人分配方案进行了调整，从种植金盏菊和三色堇的工人中分别抽调1人种植矮牵牛，这样乙地花卉种植的天数比甲地少且恰好为整数，则乙地种植金盏菊和三色堇的工人人数之比为.

查看试题解析
13. 某店三八节推出A，B，C三种花束，每种花束的成本分别为105元/束，135元/束，70元/束.在3月7日，A，B，C三种花束的单价之比为 $3 ： 4 ： 2$ ，销量之比为 $1 ： 1 ： 3$ .在3月8日，由于供不应求，该花店适当调整价格，预计3月8日三种花束的销售额将比3月7日有所增加.A，C花束增加的销售额之比为 $1 ： 2$ ；3月8日B花束的单价上调25%且A，B花束的销售额之比为 $4 ： 5$ .同时三种花束的销量之比不变，若3月8日三种花束的单价之和比3月7日三种花束的单价之和多96元，则3月8日当天的利润率为.

查看试题解析

三、解答题

14. 若(3a+2b-c)²与 $| 2 a + b | + | 2 b + c |$ 互为相反数，求a、b、c的值．

查看试题解析
15. 已知关于x、y的方程 $y = a x^{2} + b x + c ， x = 1 ， y = - 2 ， x = 3 ， y = 8$ 和 $x = - 1 ， y = - 4$ 都是方程的解．求a、b、c的值．

查看试题解析

四、综合题

16. 在中国进出口商品交易会上，某陶瓷企业出售了 $A$ ， $B$ ， $C$ 三种产品．已知出售1件 $A$ 产品和2件 $B$ 产品共收入900元，出售2件 $A$ 产品和3件 $B$ 产品共收入1600元．

(1)、求 $A$ 产品和 $B$ 产品的单价；

(2)、若出售 $A$ ， $B$ 两种产品（均有销售）共收入2400元，则出售 $A$ ， $B$ 两种产品各几件？

(3)、为推广产品，该企业开展促销活动：每出售一件 $A$ 产品，赠送2件 $C$ 产品．某客户欲购买 $A$ ， $B$ ， $C$ 三种产品共50件，并要求 $B$ 产品的件数是 $A$ 产品的1.5倍， $A$ 产品至少10件．企业赠送的 $C$ 产品不能满足客户的需求，客户还需要另行购买部分 $C$ 产品，若 $C$ 产品单价为100元，求客户支付的总金额．

查看试题解析
17. 阅读感悟：
有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：

已知实数x、y满足 $3 x - y = 5$ ①， $2 x + 3 y = 7$ ②，求 $x - 4 y$ 和 $7 x + 5 y$ 的值.

本题常规思路是将①②两式联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案，常规思路运算量比较大.其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由 $① - ②$ 可得 $x - 4 y = - 2$ ，由 $① + ② \times 2$ 可得 $7 x + 5 y = 19$ .这样的解题思想就是通常所说的“整体思想”.

解决问题：

(1)、已知二元一次方程组 ${\begin{matrix} 2 x + y = 7 \\ x + 2 y = 8 \end{matrix}$ ，则 $x - y =$ ；

(2)、某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买5支铅笔、5块橡皮、5本日记本共需元.

(3)、对于实数x、y，定义新运算： $x * y = a x + b y + c$ ，其中a、b、c是常数，等式右边是通常的加法和乘法运算，已知 $3 * 5 = 15$ ， $4 * 7 = 28$ ，那么 $1 * 1 =$ .

查看试题解析