2023-2024学年湘教版初中数学七年级下册 1.4 三元一次方程组同步分层训练基础题

试卷更新日期：2024-01-26 类型：同步测试

进入出卷网下载

一、选择题

1. 已知方程组 ${\begin{array}{l} x + y = 3 \\ y + z = - 6 \\ z + x = 9 \end{array}$ ，则 $x + y + z$ 的值是（）

A、 $3$ B、 $4$ C、 $5$ D、 $6$

查看试题解析
2. 解三元一次方程组 ${\begin{cases} x - y + z = - 3 ， ① \\ x + 2 y - z = 1 ， ② \\ x + y = 0 ， ③ \end{cases}$ 要使解法较为简便，首先应进行的变形为（）

A、①+② B、①-② C、①+③ D、②-③

查看试题解析
3. 方程组 ${\begin{cases} x + y = - 1 \\ x + z = 0 \\ y + z = 1 \end{cases}$ 的解是（）

A、 ${\begin{cases} x = - 1 \\ y = 1 \\ z = 0 \end{cases}$ B、 ${\begin{cases} x = 1 \\ y = 0 \\ z = - 1 \end{cases}$ C、 ${\begin{cases} x = 0 \\ y = 1 \\ z = - 1 \end{cases}$ D、 ${\begin{cases} x = - 1 \\ y = 0 \\ z = 1 \end{cases}$

查看试题解析
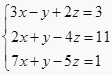4. 解方程组，若要使计算简便，消元的方法应选取（）

A、先消去x B、先消去y C、先消去z D、以上说法都不对

查看试题解析
5. 已知实数x，y，z满足 ${\begin{array}{l} x + y + z = 7 \\ 4 x + y - 2 z = 2 \end{array}$ ，则代数式3(x﹣z)+1的值是（）

A、﹣2 B、﹣4 C、﹣5 D、﹣6

查看试题解析
6. 《九章算术》是我国古代著名的数学专著，其“方程”章中给出了“遍乘直除”的算法解方程组．比如对于方程组， ${\begin{array}{l} 3 x + 2 y + z = 39 ① \\ 2 x + 3 y + z = 34 ② \\ x + 2 y + 3 z = 26 ③ \end{array}$ ，先将方程①中的未知数系数排成数列 $32139$ ，然后执行如下步骤：（如图）第一步，将方程②中的未知数系数乘以3，然后不断地减一行，直到第二行第一个数变为0；第二步，对第三行做同样的操作，其余步骤都类似．
方程①： $32139$
第一步方程②： $23134 \to 693102 ⋯ ⋯ \to 051 a$
第二步方程③： $12326 \to M ⋯ ⋯ \to 0 b 839$
其实以上步骤的本质就是在消元，根据以上操作，有下列结论：（1）数列M为： $369618$ （2） $a ＝ 24$ （3） $b ＝ 4$ 其中正确的有（）

A、（1）（2） B、（2）（3） C、（1）（3） D、（1）（2）（3）

查看试题解析
7. 我国古代数学家张丘建在《张丘建算经）里，提出了“百钱买百鸡”这个有名的数学问题.用100个钱买100只鸡，公鸡每只五个钱，母鸡每只三个钱，小鸡每个钱三只.问公鸡，小鸡各买了多少只？在这个问题中，小鸡的只数不可能是（）

A、87 B、84 C、81 D、78

查看试题解析

二、填空题

8. 已知 $a ， b ， c$ 是非负整数，且同时满足 $a + b + 2 c = 50 ， \frac{1}{3} a - b - c = 10$ ，则 $a + b - 4 c$ $=$ .

查看试题解析
9. 在一家水果店，小明买了1斤苹果，4斤西瓜，2斤橙子，共付30元；小惠买了2斤苹果，6斤西瓜，2斤橙子，共付44元．则买1斤苹果和2斤西瓜一共需付元．

查看试题解析
10. 已知x，y，z为实数，满足 ${\begin{array}{l} x + 2 y - z = 6 \\ x - y + 2 z = 3 \end{array}$ ，那么x²+y²+z²的最小值是

查看试题解析
11. 某超市销售糖果，将 $A$ 、 $B$ 、 $C$ 三种糖果搭配成甲、乙、丙三种礼盒方式销售，每个礼盒的成本分别为礼盒中 $A$ 、 $B$ 、 $C$ 糖果的成本之和，礼盒成本忽略不计.甲种礼盒每盒分别装有 $A$ 、 $B$ 、 $C$ 三种糖果 $7 k g$ 、 $2 k g$ 、 $1 k g$ ，乙种礼盒每盒分别装有 $A$ 、 $B$ 、 $C$ 三种糖果 $1 k g$ 、 $6 k g$ 、 $3 k g$ ，每盒甲的成本是每千克 $A$ 成本的12倍，每盒甲的销售利润率为25%，每盒甲的售价比每盒乙的售价低 $\frac{1}{6}$ ，丙每盒在成本上提高30%标价后打九折销售获利为每千克 $A$ 成本的1.7倍，当销售甲、乙、丙三种礼盒的数量之比为 $2 ： 1 ： 4$ 时，销售的总利润率为.（用百分数表示）

查看试题解析
12. 把一个四位数 $N$ 的各个数位上的数字 $($ 均不为零 $)$ 之和记为 $G (N)$ ，把 $N$ 的千位数字与百位数字的乘积记为 $P (N)$ ，十位数字与个位数字的乘积记为 $Q (N)$ ，称 $| \frac{G (N)}{P (N) - Q (N)} |$ 为 $N$ 的“陪伴值”．

(1)、 $4164$ 的“陪伴值”为；

(2)、若 $N$ 的千位与个位数字之和能被 $9$ 整除，且 $G (N) = 16$ ， $N$ 的“陪伴值”为 $4$ ，则满足条件的 $N$ 的最小值是．

查看试题解析

三、解答题

13. 购买铅笔7支，作业本3本，圆珠笔1支共需6元；购买铅笔10支，作业本4本，圆珠笔1支共需8元.求购买铅笔11支，作业本5本，圆珠笔2支共需多少元.

查看试题解析
14. “整体思想”是数学解题中的一种重要的思想方法．数学课上，李老师给出了一个问题，已知实数x ， y满足 ${\begin{cases} 3 x - y = 5 \\ 2 x + 3 y = 7 \end{cases}$ ，求x-4y和7x+5y的值．
小天：利用消元法解方程组，得x ， y的值后，再代入求x-4y和7x+5y的值；

小红：发现两个方程相同未知数系数之间的关系，通过适当变形，整体求得代数式的值，3x-y＝5①，2x+3y＝7②，由①-②可得x-4y＝-2，由①+②×2可得7x+5y＝19；

李老师对两位同学的讲解进行点评，指出小红同学的思路体现了数学中“整体思想”的运用．请你参考小红同学的做法，解决下面的问题：

(1)、已知二元一次方程组 ${\begin{cases} 2 x + y = 4 \\ x + 2 y = 5 \end{cases}$ ，则x-y＝， x+y＝；

(2)、请说明在关于x ， y的方程组 ${\begin{cases} x + 3 y = 4 - a \\ x - 5 y = 3 a \end{cases}$ 中，无论a为何值，x+y的值始终不变；

(3)、八年级（1）班开展安全教育知识竞赛需购买奖品，若买3支铅笔、5块橡皮、1本笔记本共需21元；若买4支铅笔、7块橡皮、1本笔记本共需28元，则购买10支铅笔、10块橡皮、10本笔记本共需多少元？（直接写出结果）

查看试题解析

四、综合题

15. 已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ ，求 $- 2 x + y + 4 z$ 的值.
小明凑出“ $- 2 x + y + 4 z = 2 \times (x + 2 y + 3 z) + (- 1) \times (4 x + 3 y + 2 z) = 20 - 15 = 5$ ”，虽然问题获得解决，但他觉得凑数字很辛苦！他问数学老师丁老师有没有不用凑数字的方法，丁老师提示道：假设 $- 2 x + y + 4 z = m (x + 2 y + 3 z) + n (4 x + 3 y + 2 z)$ ，对照方程两边各项的系数可列出方程组 ${\begin{array}{l} m + 4 n = - 2 \\ 2 m + 3 n = 1 \\ 3 m + 2 n = 4 \end{array}$ 它的解就是你凑的数！

(1)、根据丁老师的提示，已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 3 \\ 4 x + 3 y + 2 z = 7 \end{array}$ ，求 $2 x + 5 y + 8 z$ 的值.

(2)、已知 $2 a - b + k c = 4$ ，且 $a + 3 b + 2 c = - 2$ ，当k为时， $8 a + 3 b - 2 c$ 为定值，此定值是.（直接写出结果）

查看试题解析
16. 数学活动：探究不定方程
小北，小仑两位同学在学习方程过程中，发现三元一次方程组 ${\begin{array}{l} 3 x + 2 y + z = 9 \\ 2 x + 3 y + 4 z = 11 \end{array} \begin{array}{l} ① \\ ② \end{array}$ ，虽然解不出x，y，z的具体数值，但可以解出 $x + y + z$ 的值．

(1)、小北的方法： $② \times 3 - ① \times 2$ ，整理可得： $y =$ ；
$① \times 3 - ② \times 2$ ，整理可得： $x =$ ， ∴ $x + y + z = 4$ ．
小仑的方法： $① + ②$ ：③；∴得： $x + y + z = 4$ ．

(2)、已知 ${\begin{array}{l} 3 x + y + 2 z = 9 \\ x - 3 y - z = 3 \end{array}$ ，试求解 $x + y + z$ 的值．

(3)、学校现准备采购若干英语簿，数学簿以及作文本，已知采购4本英语簿，5本数学簿，2本作文本需要6元；采购4本英语簿，8本数学簿，2本作文本需要7.2元，那么采购200本英语簿，300本数学簿，100本作文本需要多少钱？

查看试题解析