高中数学三轮复习（直击痛点）：专题3导数中函数的构造问题

试卷更新日期：2024-01-26 类型：三轮冲刺

进入出卷网下载

一、选择题

1. 已知 $a = t a n \frac{1}{2}$ ， $b = t a n \frac{2}{π}$ ， $c = \frac{\sqrt{3}}{π}$ ，则（）

A、 $a < c < b$ B、 $c < a < b$ C、 $a < b < c$ D、 $b < c < a$

查看试题解析
2. 定义在 $R$ 上函数 $f (x)$ 满足 $f (- x) = f (x)$ ，且对任意的不相等的实数 $x_{1} ， x_{2} \in [0 ， + \infty)$ 有 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ 成立，若关于x的不等式 $f (2 m x - ln x - 3) \geq 2 f (3) - f (- 2 m x + ln x + 3)$ 在 $x \in [1 ， 3]$ 上恒成立，则实数m的取值范围是（）

A、 $[\frac{1}{2 e} ， 1 + \frac{ln 6}{6}]$ B、 $[\frac{1}{2 e} ， 1 + \frac{ln 3}{6}]$ C、 $[\frac{1}{e} ， 2 + \frac{ln 3}{3}]$ D、 $[\frac{1}{e} ， 2 + \frac{ln 6}{3}]$

查看试题解析
3. 已知函数 $y = a - 2 l n x ， (\frac{1}{e} \leq x \leq e)$ 的图象上存在点 $M$ ，函数 $y = x^{2} + 1$ 的图象上存在点 $N$ ，且 $M$ ， $N$ 关于 $x$ 轴对称，则 $a$ 的取值范围是（）

A、 $[1 - e^{2} ， - 2]$ B、 $[- 3 - \frac{1}{e^{2}} ， + \infty]$ C、 $[- 3 - \frac{1}{e^{2}} ， - 2]$ D、 $[1 - e^{2} ， - 3 - \frac{1}{e^{2}}]$

查看试题解析
4. 已知函数 $f (x) = e^{x} - \frac{x^{2}}{2}$ ，过点 $(m ， n)$ 作 $f (x)$ 的切线 $l$ ，若 $n = m + 1$ （ $n \neq 1$ ），则直线 $l$ 的条数为（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析
5. 若函数 $f (x) = \frac{1}{3} x^{3} - a x^{2} + x + 1$ 在区间 $(0 ， 2)$ 上存在极小值点，则a的取值范围为（）

A、 $(1 ， \frac{5}{4})$ B、 $[1 ， \frac{5}{4})$ C、 $[\frac{5}{4} ， 2)$ D、 $(1 ， + \infty)$

查看试题解析

二、多项选择题

6. 若函数 $f (x) = a l n x + \frac{b}{x} + \frac{c}{x^{2}} ， (a \neq 0)$ 既有极大值也有极小值，则（）

A、 $b c < 0$ B、 $a b < 0$ C、 $b^{2} + 8 a c > 0$ D、 $a c < 0$

查看试题解析
7. 设 $x_{1} ， x_{2}$ 分别为函数 $f (x) = \frac{x^{2}}{2} - (a + 1) x + a l n x$ 的极大值点和极小值点，且 $x_{1} < 1$ ，则下列说法正确的是（）

A、 $x = 1$ 为 $f (x)$ 的极小值点 B、 $a \in (0 ， 1) \cup (1 ， + ∞)$ C、 $f (x_{2}) \in (- \frac{3}{2} ， - \frac{1}{2})$ D、 $f (x_{1}) \in (- \frac{1}{2} ， 0)$

查看试题解析

三、填空题

8. 已知函数 $f (x) = e^{2 x} - 2 a (x - 2) e^{x} - a^{2} x^{2} (a > 0)$ 恰有两个零点，则 $a =$ .

查看试题解析
9. 设 $a \in (0 ， 1)$ ，若函数 $f (x) = a^{x} + {(1 + a)}^{x}$ 在 $(0 ， + ∞)$ 上单调递增，则a的取值范围是.

查看试题解析
10. 公园修建斜坡，假设斜坡起点在水平面上，斜坡与水平面的夹角为 $θ$ ，斜坡终点距离水平面的垂直高度为4米，游客每走一米消耗的体能为 $(1.025 - c o s θ)$ ，要使游客从斜坡底走到斜坡顶端所消耗的总体能最少，则 $θ =$ ；

查看试题解析

四、解答题

11. 已知函数 $f (x) = x^{3} + a x^{2} + b x (a \in R ， b \in R)$ ，其图象在点 $(1 ， 4)$ 处的切线方程为 $y = 4$ .

(1)、求函数 $f (x)$ 的解析式；

(2)、求函数 $f (x)$ 在区间 $[\frac{1}{2} ， 4]$ 上的最值.

查看试题解析
12. 已知函数 $f (x) = (\frac{1}{2} e^{x} + a) e^{x} - (a + 1) x$ ．

(1)、讨论f（x）的单调性；

(2)、证明：①当 $- 1 ＜ a ＜ - \frac{1}{2}$ 时，函数f（x）有两个零点；
②当﹣2＜a＜﹣1时，函数f（x）一个零点；请从①②中选择其一作答．

查看试题解析
13. 已知函数 $f (x) = (x - 1) e^{x - 1} - 3 l n x + a x^{2} - 1$ ， $a \in R$ .

(1)、当 $a = 1$ 时，求 $f (x)$ 在 $x = 1$ 处的切线方程；

(2)、证明： $f (x)$ 有唯一极值点.

查看试题解析
14. 已知函数 $f (x) = m e^{x} - \ln x - 1$ .

(1)、当 $m = 1$ 时，求曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线方程；

(2)、若 $m \in (1 ， + \infty)$ ，求证： $f (x) > 1$ .

查看试题解析
15. 已知函数 $f (x) = a e^{x} + l n (e a)$ .

(1)、当 $a = 1$ 时，求过点 $(- 2 ， 0)$ 且和曲线 $y = f (x)$ 相切的直线方程；

(2)、若对任意实数 $x > 1$ ，不等式 $f (x) ⩾ l n (x - 1)$ 恒成立，求实数 $a$ 的取值范围.

查看试题解析
16. 已知 $f (x) = (e^{x} - 1) s i n x$ ， $x \in (0 ， 2 π)$ ．

(1)、求 $f (x)$ 在点 $P (π ， f (π))$ 的切线方程；

(2)、设 $g (x) = f (x) - x^{2}$ ， $x \in (0 ， 2 π)$ ，判断 $g (x)$ 的零点个数，并说明理由．

查看试题解析
17. 已知函数 $f (x) = a x^{3} + 2 s i n x - x c o s x$ （其中 $a$ 为实数）．

(1)、若 $a = - \frac{1}{2} ， x \in (0 ， \frac{π}{2})$ ，证明： $f (x) \geq 0$ ；

(2)、探究 $f (x)$ 在 $(- π ， π)$ 上的极值点个数．

查看试题解析
18. 已知 $- 1 \leq a \leq 1$ ，函数 $f (x) = e^{x} - \frac{1}{2} x^{2} - a s i n x - 1$ ， $g (x) = f (x) + f (- x)$ .

(1)、讨论函数 $g (x)$ 的单调性；

(2)、设 $f' (x)$ 是 $f (x)$ 的导数.证明：
（i） $f (x)$ 在 $R$ 上单调递增；
（ii）当 $x \in [- \frac{π}{3} ， \frac{π}{3}]$ 时，若 $| f' (x) | \leq M$ ，则 $| f (x) | \leq M$ .

查看试题解析
19. 设 $f (x) = \frac{x}{l n x}$

(1)、求证： $f (x) < \frac{x^{2}}{x - 1}$ ；

(2)、若 $f (x) < n l n (1 - x^{2})$ 恒成立，求整数 $n$ 的最大值．（参考数据 $l n 2 \approx 0.693$ ， $l n 3 \approx 1.099$ ）

查看试题解析
20. 设函数 $f (x) = x - x^{3} e^{a x + b}$ ，曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线方程为 $y = - x + 1$ ．

(1)、求 $a ， b$ 的值；

(2)、设函数 $g (x) = f^{'} (x)$ ，求 $g (x)$ 的单调区间；

(3)、求 $f (x)$ 的极值点个数．

查看试题解析
21. 已知函数 $f (x) = (\frac{1}{x} + \frac{1}{2}) l n (x + 1)$ ．

(1)、求曲线 $y = f (x)$ 在 $x = 2$ 处切线的斜率；

(2)、当 $x > 0$ 时，证明： $f (x) > 1$ ；

(3)、证明： $\frac{5}{6} < l n (n!) - (n + \frac{1}{2}) l n (n) + n \leq 1$ ．

查看试题解析
22. 已知函数 $f (x) = (\frac{1}{x} + a) l n (1 + x)$ .

(1)、当 $a = - 1$ 时，求曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线方程；

(2)、是否存在a，b，使得曲线 $y = f (\frac{1}{x})$ 关于直线 $x = b$ 对称，若存在，求a，b的值，若不存在，说明理由.

(3)、若 $f (x)$ 在 $(0 ， + ∞)$ 存在极值，求a的取值范围.

查看试题解析
23. 已知函数 $f (x) = (\frac{1}{x} + a) l n (1 + x)$ .

(1)、当 $a = - 1$ 时，求曲线 $y = f (x)$ 在点 $(1 ， f (x))$ 处的切线方程.

(2)、若函数 $f (x)$ 在 $(0 ， + ∞)$ 单调递增，求 $a$ 的取值范围.

查看试题解析
24. 已知 $f (x) = l n x$ ，取点 $(a_{1} f (a_{1}))$ 过其曲线 $y = f (x)$ 作切线交 $y$ 轴于 $(0 ， a_{2})$ ，取点 $(a_{2} f (a_{2}))$ 过其曲线 $y = f (x)$ 作切线交 $y$ 轴于 $(0 ， a_{3})$ ，若 $a_{3} > 0$ 则继续，若 $a_{3} \leq 0$ 则停止，以此类推得到数列 ${a_{n}}$ .

(1)、若正整数 $m \geq 2$ ，证明 $a_{m} = l n a_{m - 1} - 1$ ；

(2)、若正整数 $m \geq 2$ ，试比较 $a_{m}$ 与 $a_{m - 1} - 2$ 大小；

(3)、若正整数 $k \geq 3$ ，是否存在 $k$ 使得 $a_{1} ， a_{2} ， a_{3} ⋯ a_{k}$ 依次成等差数列?若存在，求出 $k$ 的所有取值，若不存在，请说明理由.

查看试题解析
25. 已知函数 $f (x) = 4 x - x^{4}$ ， $x \in R，$ 问
（1）求 f x 的单调区间（2）设曲线 y = f x 与 x 轴正半轴的交点为 $P$ ，曲线在点 P 处的切线方程为 y = $g (x)$ ，求证：对于任意的正实数 x ，都有 $f (x)$ ∈ $g (x)$

(1)、求 $f (x)$ 的单调区间

(2)、设曲线 $y = f (x)$ 与 $x$ 轴正半轴的交点为 $P$ ，曲线在点 $P$ 处的切线方程为 $y = g (x)$ ，求证：对于任意的正实数 $x$ ，都有 $f (x) \in g (x)$ ；

(3)、若方程 $f (x) = a$ （ $a$ 为实数）有两个正实数根 $x_{1} ， x_{2}$ 且 $x_{1} < x_{2}$ ，求证： $x_{2} - x_{1} < - \frac{a}{3} + 4^{\frac{1}{3}}$ .

查看试题解析
26. 已知函数 $f (x) = \ln \frac{1 + x}{1 - x}$ ．
（Ⅰ）求曲线 $y = f (x)$ 在点 $(0 ， f (0))$ 处的切线方程；
（Ⅱ）求证：当 $x \in (0 ， 1)$ 时， $f (x) > 2 (x + \frac{x^{3}}{3})$ ；
（Ⅲ）设实数k使得 $f (x) > k (x + \frac{x^{3}}{3})$ 对 $x \in (0 ， 1)$ 恒成立，求k的最大值．

查看试题解析
27. 某地准备在山谷中建一座桥梁，桥址位置的竖直截面图如图所示：谷底O在水平线MN上、桥AB与MN平行， $O O^{'}$ 为铅垂线( $O^{'}$ 在AB上).经测量，左侧曲线AO上任一点D到MN的距离 $h_{1}$ (米)与D到 $O O^{'}$ 的距离a(米)之间满足关系式 $h_{1} = \frac{1}{40} a^{2}$ ；右侧曲线BO上任一点F到MN的距离 $h_{2}$ (米)与F到 $O O^{'}$ 的距离b(米)之间满足关系式 $h_{2} = - \frac{1}{800} b^{3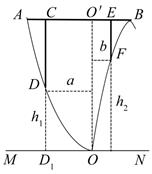} + 6 b$ .已知点B到 $O O^{'}$ 的距离为40米.

(1)、求桥AB的长度；

(2)、计划在谷底两侧建造平行于 $O O^{'}$ 的桥墩CD和EF，且CE为80米，其中C，E在AB上(不包括端点).桥墩EF每米造价k(万元)、桥墩CD每米造价 $\frac{3}{2} k$ (万元)(k>0).问 $O^{'} E$ 为多少米时，桥墩CD与EF的总造价最低?

查看试题解析