2023-2024学年人教版(吉林地区)初中数学九年级下册 27.2.3 相似三角形应用举例同步分层训练培优题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 图,电灯在横杆的正上方,在灯光下的影子为 , , 米,米,点到的距离是2.4米,则到的距离为( )
 A、3.6米 B、4米 C、5米 D、5.4米2. 如图,放映幻灯片时通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为( )
A、3.6米 B、4米 C、5米 D、5.4米2. 如图,放映幻灯片时通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为( ) A、6cm B、12cm C、18cm D、24cm3. 路边有一根电线杆AB和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处,而长方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,长方形广告牌的长HF=4米,高HC=3米,DE=4米,则电线杆AB的高度是( )
A、6cm B、12cm C、18cm D、24cm3. 路边有一根电线杆AB和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处,而长方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,长方形广告牌的长HF=4米,高HC=3米,DE=4米,则电线杆AB的高度是( ) A、6.75米 B、7.75米 C、8.25米 D、10.75米4. 如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为( )
A、6.75米 B、7.75米 C、8.25米 D、10.75米4. 如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为( ) A、0.36 平方米 B、0. 81 平方米 C、2 平方米 D、3.24 平方米5. 如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1 m,继续往前走3 m到达E处时,测得影子EF的长为2 m.已知王华的身高是1.5 m,那么路灯A的高度AB等于( )
A、0.36 平方米 B、0. 81 平方米 C、2 平方米 D、3.24 平方米5. 如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1 m,继续往前走3 m到达E处时,测得影子EF的长为2 m.已知王华的身高是1.5 m,那么路灯A的高度AB等于( ) A、4.5 m B、6 m C、7.2 m D、8 m6.
A、4.5 m B、6 m C、7.2 m D、8 m6.如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )
 A、
A、 B、
B、 C、
C、 D、
D、 7. 如图▱ABCD,F为BC中点,延长AD至E,使 ,连结EF交DC于点G,则 =( )
7. 如图▱ABCD,F为BC中点,延长AD至E,使 ,连结EF交DC于点G,则 =( )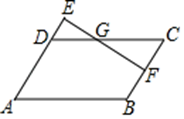 A、2:3 B、3:2 C、9:4 D、4:98. 如图,将 沿 边上的中线 平移到 的位置.已知 的面积为16,阴影部分三角形的面积9.若 ,则 等于( )
A、2:3 B、3:2 C、9:4 D、4:98. 如图,将 沿 边上的中线 平移到 的位置.已知 的面积为16,阴影部分三角形的面积9.若 ,则 等于( ) A、2 B、3 C、4 D、
A、2 B、3 C、4 D、二、填空题
-
9. 如图,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退,直到她刚好在镜子中看到旗杆的顶端,已知小艺的眼睛离地面高度为1.6米,同时量得小艺与镜子的水平距离为2米,镜子与旗杆的水平距离为10米.则旗杆的高度为 米.
 10. 如图,小亮同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是7米(即OD=7米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是 米.
10. 如图,小亮同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是7米(即OD=7米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是 米. 11. 据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第一个小孔成像的实验,阐释了光的直线传播原理,如图①所示.如图②所示的小孔成像实验中,若物距为 , 像距为 , 蜡烛火焰倒立的像的高度是 , 则蜡烛火焰的高度是 .
11. 据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第一个小孔成像的实验,阐释了光的直线传播原理,如图①所示.如图②所示的小孔成像实验中,若物距为 , 像距为 , 蜡烛火焰倒立的像的高度是 , 则蜡烛火焰的高度是 .

图① 图②
12. 如图,‘ABC中,AB=AC , AD」BC于点D,DE平分经ADC , 交AC与点E,EF」AB于点F,且交AD-于点G,若AG=2,BC=12,则AD= , AF=.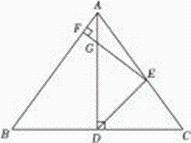 13. 如图,等腰三角形.点在BC上,AC沿AD翻折交BC于点 , 点在AB上,EB沿EF翻折,使得在一条直线上.若 , 则CE的值为.
13. 如图,等腰三角形.点在BC上,AC沿AD翻折交BC于点 , 点在AB上,EB沿EF翻折,使得在一条直线上.若 , 则CE的值为.
三、解答题
-
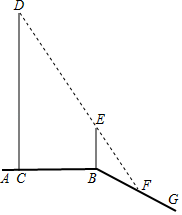
14. 如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
 15. 如图,在矩形中, , , 动点从点开始以每秒2个单位长度沿向终点运动,同时,动点从点开始沿以每秒3个单位长度向终点运动,它们同时到达终点.连接交于点 . 过点作 , 交直线于点 .
15. 如图,在矩形中, , , 动点从点开始以每秒2个单位长度沿向终点运动,同时,动点从点开始沿以每秒3个单位长度向终点运动,它们同时到达终点.连接交于点 . 过点作 , 交直线于点 .
备用图
(1)、当点在线段上时,求证: .(2)、当时,求的面积.(3)、在 , 的运动过程中,是否存在某一位置,使得以点 , , 为顶点的三角形与相似?若存在,求的长;若不存在,请说明理由.四、综合题
-
16. 我国古代数学家赵爽利用影子对物体进行测量的方法,至今仍有借鉴意义.如图1,身高的小王晚上在路灯灯柱下散步,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部A向东走20步到M处,发现自己的影子端点落在点P处,作好记号后,继续沿刚才自己的影子走4步恰好到达点P处,此时影子的端点在点Q处,已知小王和灯柱的底端在同一水平线上,小王的步间距保持一致.
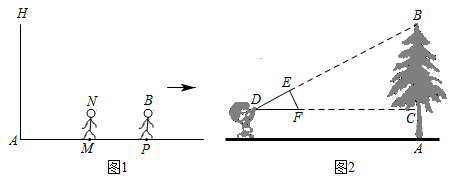 (1)、请在图中画出路灯O和影子端点Q的位置.(2)、估计路灯的高,并求影长的步数.(3)、无论点光源还是视线,其本质是相同的,日常生活中我们也可以直接利用视线解决问题.如图2,小明同学用自制的直角三角形纸板测量树的高度 , 他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.测得 , , , 小明眼睛到地面的距离为 , 则树高为m.17. 如图,是的直径,点在圆上,点在圆外,点和点在直径的同侧,与相交于点 .
(1)、请在图中画出路灯O和影子端点Q的位置.(2)、估计路灯的高,并求影长的步数.(3)、无论点光源还是视线,其本质是相同的,日常生活中我们也可以直接利用视线解决问题.如图2,小明同学用自制的直角三角形纸板测量树的高度 , 他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.测得 , , , 小明眼睛到地面的距离为 , 则树高为m.17. 如图,是的直径,点在圆上,点在圆外,点和点在直径的同侧,与相交于点 .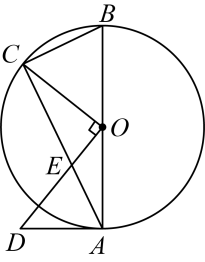 (1)、求证:是的切线;(2)、若的半径为4, , 求的面积.
(1)、求证:是的切线;(2)、若的半径为4, , 求的面积.