2023-2024学年人教版(吉林地区)初中数学九年级下册 27.2.3 相似三角形应用举例同步分层训练提升题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 如图,为测量学校旗杆的高度,小明用长为3.2m的竹竿作测量工具,移动竹竿,使竹竿顶端与旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )
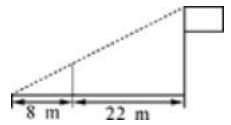 A、8.8m B、10m C、12m D、14m2. 如图,身高的小亮站在某路灯下,发现自己的影长恰好是 , 经测量,此时小亮离路灯底部的距离是 , 则路灯离地面的高度AB是( )
A、8.8m B、10m C、12m D、14m2. 如图,身高的小亮站在某路灯下,发现自己的影长恰好是 , 经测量,此时小亮离路灯底部的距离是 , 则路灯离地面的高度AB是( )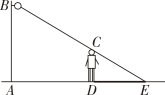 A、 B、 C、 D、3. 同一时刻,同一地点,在阳光下影长为0.4米的小王身高为1.6米,一棵树的影长为3.2米,则这棵树的高度为 ( )A、0.8米 B、6.4米 C、12.8米 D、25.6米4. 《九章算术》的“勾股”章中有这样一个问题:“今有邑方不知大小,各中开门.出北门二十步有木.出南门十四步,折而西行一千七百七十五步见木.问邑方几何.”大意是:如图所示,四边形是一座正方形小城,北门位于的中点,南门位于的中点.从北门出去正北方向20步远的处有一树木.从南门出去向南行走14步,再向西行走1775步,恰好能看见处的树木.正方形小城的边长为( )
A、 B、 C、 D、3. 同一时刻,同一地点,在阳光下影长为0.4米的小王身高为1.6米,一棵树的影长为3.2米,则这棵树的高度为 ( )A、0.8米 B、6.4米 C、12.8米 D、25.6米4. 《九章算术》的“勾股”章中有这样一个问题:“今有邑方不知大小,各中开门.出北门二十步有木.出南门十四步,折而西行一千七百七十五步见木.问邑方几何.”大意是:如图所示,四边形是一座正方形小城,北门位于的中点,南门位于的中点.从北门出去正北方向20步远的处有一树木.从南门出去向南行走14步,再向西行走1775步,恰好能看见处的树木.正方形小城的边长为( ) A、105步 B、200步 C、250步 D、305步5. 凸透镜成像的原理如因所示,.若物体到焦点的距离与焦点到凸透镜中心线DB的弫离之比为5:4,则物体被缩小到原来的( )
A、105步 B、200步 C、250步 D、305步5. 凸透镜成像的原理如因所示,.若物体到焦点的距离与焦点到凸透镜中心线DB的弫离之比为5:4,则物体被缩小到原来的( ) A、 B、 C、 D、6. 大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为10cm , 像距为15cm , 蜡烛火焰倒立的像的高度是8cm , 则蜡烛火焰的高度是( )cm .
A、 B、 C、 D、6. 大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为10cm , 像距为15cm , 蜡烛火焰倒立的像的高度是8cm , 则蜡烛火焰的高度是( )cm . A、 B、6 C、 D、87. 某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5米的标杆DF,如图所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影子BC的长度为6米,则旗杆AC的高度为( ).
A、 B、6 C、 D、87. 某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5米的标杆DF,如图所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影子BC的长度为6米,则旗杆AC的高度为( ). A、6米 B、7米 C、8.5米 D、9米8. 如图,一张等腰三角形纸片,底边长为15cm,底边上的高线长为22.5cm.现沿底边依次从下往上裁剪宽度均为3 cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( ).
A、6米 B、7米 C、8.5米 D、9米8. 如图,一张等腰三角形纸片,底边长为15cm,底边上的高线长为22.5cm.现沿底边依次从下往上裁剪宽度均为3 cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( ). A、第4张 B、第5张 C、第6张 D、第7张
A、第4张 B、第5张 C、第6张 D、第7张二、填空题
-
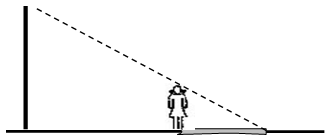
9. 如图,已知小丽的身高是1.6米,他在路灯下的影长为2米,小丽距路灯灯杆的底部3米,那么路灯灯泡距地面的高度是米.
 10. 如图1是液体沙漏的立体图形,图2,图3分别是液体沙漏某一时刻沙漏上半部分液体长度与液面距离水平面高度的平面示意图,则图3中AB=cm.
10. 如图1是液体沙漏的立体图形,图2,图3分别是液体沙漏某一时刻沙漏上半部分液体长度与液面距离水平面高度的平面示意图,则图3中AB=cm.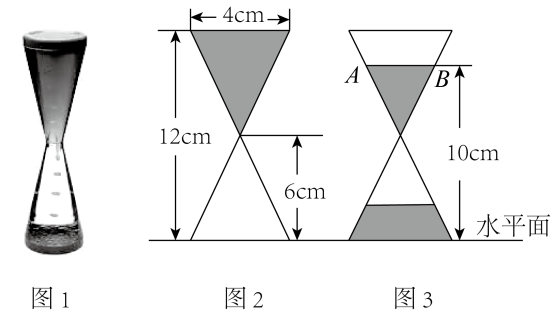 11. 某数学兴趣小组测量校园内一棵树的高度,采用以下方法:如图,把支架(EF)放在离树(AB)适当距离的水平地面上的点F处,再把镜子水平放在支架(EF)上的点E处,然后沿着直线BF后退至点D处,这时恰好在镜子里看到树的顶端A , 再用皮尺分别测量BF , DF , EF , 观测者目高(CD)的长,利用测得的数据可以求出这棵树的高度.已知CD⊥BD于点D , EF⊥BD于点F , AB⊥BD于点B , BF=6米,DF=2米,EF=0.5米,CD=1.7米,则这棵树的高度(AB的长)是 米.
11. 某数学兴趣小组测量校园内一棵树的高度,采用以下方法:如图,把支架(EF)放在离树(AB)适当距离的水平地面上的点F处,再把镜子水平放在支架(EF)上的点E处,然后沿着直线BF后退至点D处,这时恰好在镜子里看到树的顶端A , 再用皮尺分别测量BF , DF , EF , 观测者目高(CD)的长,利用测得的数据可以求出这棵树的高度.已知CD⊥BD于点D , EF⊥BD于点F , AB⊥BD于点B , BF=6米,DF=2米,EF=0.5米,CD=1.7米,则这棵树的高度(AB的长)是 米.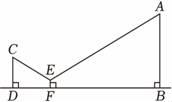 12. 如图,在正方形中,是边上的一点,连接交于点 , 连接并延长交于点 .
12. 如图,在正方形中,是边上的一点,连接交于点 , 连接并延长交于点 .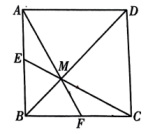 (1)、若是的中点,则;(2)、若 , 则 .13. 如图,某公园有一月牙形水池,水池边缘有A , B , C , D , E五盏装饰灯.为了估测该水池的大小,观测员在A , D两点处发现点A , E , C和D , E , B均在同一直线上,沿AD方向走到F点,发现 . 测得米,米,米,则所在圆的半径为米,所在圆的半径为.米.
(1)、若是的中点,则;(2)、若 , 则 .13. 如图,某公园有一月牙形水池,水池边缘有A , B , C , D , E五盏装饰灯.为了估测该水池的大小,观测员在A , D两点处发现点A , E , C和D , E , B均在同一直线上,沿AD方向走到F点,发现 . 测得米,米,米,则所在圆的半径为米,所在圆的半径为.米.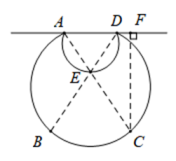
三、解答题
-
14. 一天晚上,小南和小北利用灯光下的影子来测量一路灯D的高度,如图,当朝阳走到点A处时,小南测得小北直立身高AM与其影子长AE正好相等,接着小北沿AC方向继续向前走,走到点B处时,小北直立时身高BN的影子恰好是线段AB,并测得.已知小北直立时的身高为1.5m,求路灯的高CD的长.
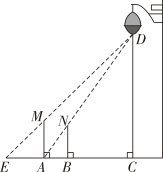 15. 已知:如图,和是直立在地面上的两根立柱, , 某一时刻,在阳光下的投影 .
15. 已知:如图,和是直立在地面上的两根立柱, , 某一时刻,在阳光下的投影 . (1)、请你在图中画出此时在阳光下的投影,并简述画图步骤和说明作图依据了太阳光线的哪一性质;(2)、在测量的投影长时,同时测出在阳光下的投影长为 , 请你计算的长.
(1)、请你在图中画出此时在阳光下的投影,并简述画图步骤和说明作图依据了太阳光线的哪一性质;(2)、在测量的投影长时,同时测出在阳光下的投影长为 , 请你计算的长.四、综合题
-
16. 如图,在锐角三角形中,为边的中点,为边所在的直线上一点,连接交延长线于 , 已知 , 问:
 (1)、点此时的位置;(2)、求的值.17. 【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内:反射光线和入射光线分别位于法线两例;入反射角r等于入射角i.这就是光的反射定律.
(1)、点此时的位置;(2)、求的值.17. 【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内:反射光线和入射光线分别位于法线两例;入反射角r等于入射角i.这就是光的反射定律.【问题解决】如图2,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙,木板和平面镜,手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点E到地面的高度 , 点F到地面的高度 , 灯泡到木板的水平距离 , 木板到墙的水平距离为.图中A,B,C,D在同一条直线上.
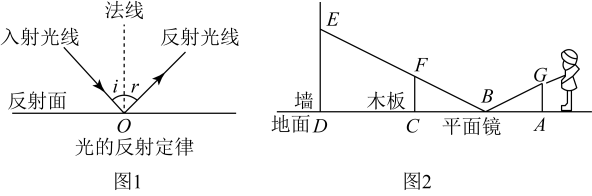 (1)、求的长;(2)、求灯泡到地面的高度.
(1)、求的长;(2)、求灯泡到地面的高度.