2023-2024学年人教版(吉林地区)初中数学九年级下册 27.2.3 相似三角形应用举例同步分层训练基础题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边长为( ).A、3cm B、4cm C、4.5cm D、5cm2. 如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影子长DE=1.8m,窗户下沿到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
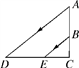 A、1.5m B、1.6m C、1.86m D、2.16m3. 如图所示,树AB在路灯的照射下形成投影AC,已知路灯高 , 树影 , 树AB与路灯的水平距离 , 则树的高度AB是( ).
A、1.5m B、1.6m C、1.86m D、2.16m3. 如图所示,树AB在路灯的照射下形成投影AC,已知路灯高 , 树影 , 树AB与路灯的水平距离 , 则树的高度AB是( ).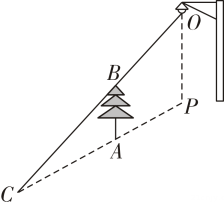 A、2m B、3m C、 D、4. 《海岛算经》是我国杰出数学家刘徽留给后世最宝贵的数学遗产.书中的第一问:今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表参相直.从前表却行一百二十三步,人目着地取望岛峰,与表末参合.从后表却行一百二十七步,人目着地取望岛峰,亦与表末参合.问岛高及去表各几何?大致意思是:假设测量海岛,立两根表,高均为3丈,前后相距1000步,令后表与前表在同一直线上,从前表退行123步,人的眼睛贴着地面观察海岛,从后表退行127步,人的眼睛贴着地面观察海岛,问海岛高度及两表相距多远?想要解决这一问题,需要利用( )A、全等三角形 B、相似三角形 C、勾股定理 D、垂径定理5. 如图,路灯距离地面8米,若身高1.6米的小明在距离路灯的底部(点O)20米的A处,则小明的影子AM的长为( )
A、2m B、3m C、 D、4. 《海岛算经》是我国杰出数学家刘徽留给后世最宝贵的数学遗产.书中的第一问:今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表参相直.从前表却行一百二十三步,人目着地取望岛峰,与表末参合.从后表却行一百二十七步,人目着地取望岛峰,亦与表末参合.问岛高及去表各几何?大致意思是:假设测量海岛,立两根表,高均为3丈,前后相距1000步,令后表与前表在同一直线上,从前表退行123步,人的眼睛贴着地面观察海岛,从后表退行127步,人的眼睛贴着地面观察海岛,问海岛高度及两表相距多远?想要解决这一问题,需要利用( )A、全等三角形 B、相似三角形 C、勾股定理 D、垂径定理5. 如图,路灯距离地面8米,若身高1.6米的小明在距离路灯的底部(点O)20米的A处,则小明的影子AM的长为( ) A、1.25米 B、5米 C、6米 D、4米6. 如图,小明设计的用激光笔测量城墙高度的示意图,在点处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙的顶端处,已知 , , 米,米,米,那么该城墙的高度为( )
A、1.25米 B、5米 C、6米 D、4米6. 如图,小明设计的用激光笔测量城墙高度的示意图,在点处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙的顶端处,已知 , , 米,米,米,那么该城墙的高度为( ) A、6 B、8 C、10 D、187. 如图,一壁厚均匀的容器外径为 , 用一个交叉卡钳(两条尺长和相等)可测量容器的内部直径.如果 , 且量得 , 则零件的厚度x为( )
A、6 B、8 C、10 D、187. 如图,一壁厚均匀的容器外径为 , 用一个交叉卡钳(两条尺长和相等)可测量容器的内部直径.如果 , 且量得 , 则零件的厚度x为( ) A、 B、 C、 D、8. 如图,一壁厚均匀的容器外径为18 , 用一个交叉卡钳(两条尺长和相等)可测量容器的内部直径.如果 , 且量得 , 则零件的厚度x为( )
A、 B、 C、 D、8. 如图,一壁厚均匀的容器外径为18 , 用一个交叉卡钳(两条尺长和相等)可测量容器的内部直径.如果 , 且量得 , 则零件的厚度x为( ) A、0.25 B、0.3 C、0.35 D、0.4
A、0.25 B、0.3 C、0.35 D、0.4二、填空题
-
9. 据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示。如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是cm.
 10. 如图,数学活动课上,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退保持脚、镜和旗杆底端在同一直线上 , 直到她刚好在镜子中看到旗杆的顶端已知小艺的眼睛离地面高度为米,同时量得小艺与镜子的水平距离为米,镜子与旗杆的水平距离为米,则旗杆的高度为 米
10. 如图,数学活动课上,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退保持脚、镜和旗杆底端在同一直线上 , 直到她刚好在镜子中看到旗杆的顶端已知小艺的眼睛离地面高度为米,同时量得小艺与镜子的水平距离为米,镜子与旗杆的水平距离为米,则旗杆的高度为 米 11. 如图,路灯距离地面6米,身高1.2米的小明站在距离路灯的底部(点O)10米的A处,则小明的影长为米.
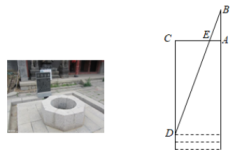
11. 如图,路灯距离地面6米,身高1.2米的小明站在距离路灯的底部(点O)10米的A处,则小明的影长为米.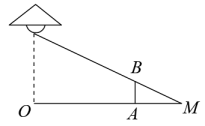 12. 《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆 , 从木杆的顶端B观察井水水岸D,视线与井口的直径交于点E,如果测得米,米,米,那么为米.
12. 《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆 , 从木杆的顶端B观察井水水岸D,视线与井口的直径交于点E,如果测得米,米,米,那么为米.
 13. 如下图,跷跷板支架的高为0.3米,是的中点,那么跷跷板能骁起的最大高度等于米.
13. 如下图,跷跷板支架的高为0.3米,是的中点,那么跷跷板能骁起的最大高度等于米.
三、解答题
-
14. 如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.
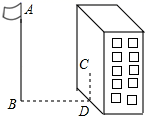 15. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C. A共线.
15. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C. A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
四、综合题
-
16. 如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度DE=3.5m,点F到地面的高度CF=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上.
 (1)、求BC的长.(2)、求灯泡到地面的高度AG.17.(1)、解方程: .(2)、为了测量校园内一棵树的高度,学校数学应用实践小组做了如下的探索实践.根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把镜子放在离树的水平地面点E处,然后一同学沿着直线后退到点D,这时该同学恰好在镜子里看到树梢顶点A,再用皮尺量得 , 该同学身高 . 请你计算树()的高度.
(1)、求BC的长.(2)、求灯泡到地面的高度AG.17.(1)、解方程: .(2)、为了测量校园内一棵树的高度,学校数学应用实践小组做了如下的探索实践.根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把镜子放在离树的水平地面点E处,然后一同学沿着直线后退到点D,这时该同学恰好在镜子里看到树梢顶点A,再用皮尺量得 , 该同学身高 . 请你计算树()的高度.