2023-2024学年人教版(吉林地区)初中数学九年级下册 27.2.2 相似三角形的性质同步分层训练基础题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 如图,中,点D , E分别在边上.若 , , 则的长为( )
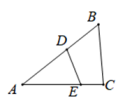 A、 B、 C、 D、32. 如图,在中, , , 若 , 则等于( )
A、 B、 C、 D、32. 如图,在中, , , 若 , 则等于( )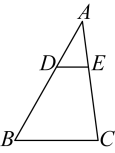 A、6 B、8 C、7 D、53. 如图所示,四边形中, , , , , , 若与相似,则符合条件的点个数是( )
A、6 B、8 C、7 D、53. 如图所示,四边形中, , , , , , 若与相似,则符合条件的点个数是( )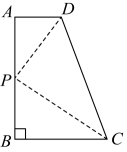 A、0 B、1 C、2 D、34. 如图,在四边形 中,以 为直径的 恰好经过点 , , 交于点 ,已知 平分 , , ,则 的值为( )
A、0 B、1 C、2 D、34. 如图,在四边形 中,以 为直径的 恰好经过点 , , 交于点 ,已知 平分 , , ,则 的值为( )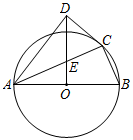 A、 B、 C、 D、5. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )
A、 B、 C、 D、5. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )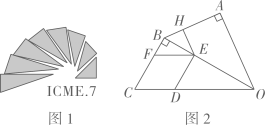 A、 B、 C、 D、6. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD,其中 , 则剪掉的两个直角三角形的斜边长不可能是( ).
A、 B、 C、 D、6. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD,其中 , 则剪掉的两个直角三角形的斜边长不可能是( ). A、 B、 C、10 D、7. 如图,在中, , 在边的延长线上取一点 , 过点的直线分别交 , 的延长线于点 , , 则下列结论一定正确的是( )
A、 B、 C、10 D、7. 如图,在中, , 在边的延长线上取一点 , 过点的直线分别交 , 的延长线于点 , , 则下列结论一定正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 已知两个三角形相似,其中一个三角形的两个角分别为
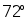 、
、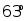 , 则另一个三角形中最小的内角为 . 9. 若两个相似三角形的相似比是1:2,则它们的周长比是 .10. 已知 , 其中顶点A、B、C分别对应顶点D、E、F , 如果 , , 那么.11. 有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点 正好在书架边框上.每本书的厚度为5cm,高度为20cm,书架宽为40cm,则 的长.
, 则另一个三角形中最小的内角为 . 9. 若两个相似三角形的相似比是1:2,则它们的周长比是 .10. 已知 , 其中顶点A、B、C分别对应顶点D、E、F , 如果 , , 那么.11. 有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点 正好在书架边框上.每本书的厚度为5cm,高度为20cm,书架宽为40cm,则 的长.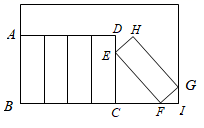 12. 如图, 中, , ,垂足为D,若AD=2,BD=4,则CD为 .
12. 如图, 中, , ,垂足为D,若AD=2,BD=4,则CD为 .
三、解答题
-
13. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,C为的中点,延长AD,BC相交于点P,连结AC.
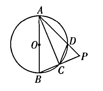 (1)、求证;AB=AP.(2)、当AB=10,DP=2时,求线段CP的长.14. 如图,内接于 , , 它的外角的平分线交于点D , 连接交于点F .
(1)、求证;AB=AP.(2)、当AB=10,DP=2时,求线段CP的长.14. 如图,内接于 , , 它的外角的平分线交于点D , 连接交于点F . (1)、若 , 求的度数.(2)、求证: .(3)、若 , 当 , 求的度数(用含的代数式表示).
(1)、若 , 求的度数.(2)、求证: .(3)、若 , 当 , 求的度数(用含的代数式表示).四、综合题

