2023-2024学年人教版(吉林地区)初中数学九年级下册 27.2.1 相似三角形的判定同步分层训练提升题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 已知 , , , 成比例线段,其中 , , , 则( )A、8cm B、9.5cm C、4cm D、4.5cm2. 小明按照以下步骤画线段AB的三等分点:
画法
图形
1.以A为端点画一条射线;
2.用圆规在射线上依次截取3条等长线段AC、CD、DE , 连接BE;
3.过点C、D分别画BE的平行线,交线段AB于点M、N , M、N就是线段AB的三等分点.
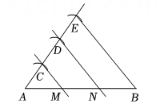
这一画图过程体现的数学依据是( )
A、两直线平行,同位角相等 B、两条平行线之间的距离处处相等 C、垂直于同一条直线的两条直线平行 D、两条直线被一组平行线所截,所得的对应线段成比例3. 已知在中,点、分别在边、上,那么下列条件中不能够判断的是( )A、 B、 C、 D、4. 如图,D是△ABC的边AB上的一点,那么下列四个条件不能单独判定△ABC∽△ACD的是( ) A、∠B=∠ACD B、∠ADC=∠ACB C、= D、AC2=AD•AB5. 如图,在中, . 将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )A、
A、∠B=∠ACD B、∠ADC=∠ACB C、= D、AC2=AD•AB5. 如图,在中, . 将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )A、 B、
B、 C、
C、 D、
D、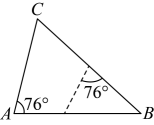 6. 如图,已知 , 那么添加下列一个条件后,仍不能判定的是( )
6. 如图,已知 , 那么添加下列一个条件后,仍不能判定的是( ) A、 B、 C、 D、7. 如图,l1∥l2∥l3 , 直线AC、DF与这三条平行线分别交于点A、B、C和点D、E、F,若AB=4,DE=3,EF=6,则AC的长是( )
A、 B、 C、 D、7. 如图,l1∥l2∥l3 , 直线AC、DF与这三条平行线分别交于点A、B、C和点D、E、F,若AB=4,DE=3,EF=6,则AC的长是( ) A、4 B、6 C、8 D、128. 如图正方形 , 点分别在边上,且 , 把绕点沿逆时针方向旋转得到 , 连接交于点 , 连接 , 并在上截取 , 连接 , 有如下结论:①;②始终平分;③;④;⑤垂直平分 , 上述结论中,所有正确的个数是( )
A、4 B、6 C、8 D、128. 如图正方形 , 点分别在边上,且 , 把绕点沿逆时针方向旋转得到 , 连接交于点 , 连接 , 并在上截取 , 连接 , 有如下结论:①;②始终平分;③;④;⑤垂直平分 , 上述结论中,所有正确的个数是( ) A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
9. 如图,在矩形中,是边的中点,连接交对角线于点 , 则的长为 .
 10. 如图,要使 , 可以添加条件∶ .
10. 如图,要使 , 可以添加条件∶ . 11. 如图,在正方形网格上,若使 , 则点P应在 .
11. 如图,在正方形网格上,若使 , 则点P应在 .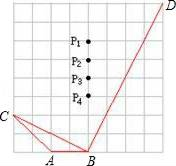 12. 直线l上的三个点A、B、C , 若满足BC=AB , 则称点C是点A关于点B的“半距点”.如图1,BC=AB , 此时点C就是点A关于点B的一个“半距点”.如图2若M、N、P三个点在同一条直线m上,且点P是点M关于点N的“半距点”,MN=6cm . 则MP=cm .
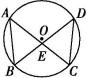
12. 直线l上的三个点A、B、C , 若满足BC=AB , 则称点C是点A关于点B的“半距点”.如图1,BC=AB , 此时点C就是点A关于点B的一个“半距点”.如图2若M、N、P三个点在同一条直线m上,且点P是点M关于点N的“半距点”,MN=6cm . 则MP=cm . 13. 如图所示,在四边形中, , , , E为的中点,连结 , 若 , 则的度数为 .
13. 如图所示,在四边形中, , , , E为的中点,连结 , 若 , 则的度数为 .
三、解答题