2023-2024学年人教版(吉林地区)初中数学八年级下册 17.2 勾股定理的逆定理同步分层训练培优题

试卷更新日期：2024-01-26 类型：同步测试

进入出卷网下载

一、选择题

1. 满足下列条件的 $△ A B C$ ，不是直角三角形的为（）

A、 $∠ A ： ∠ B ： ∠ C = 5 ： 12 ： 13$ B、 $∠ A = ∠ B - ∠ C$ C、 $b^{2} = a^{2} - c^{2}$ D、 $a ： b ： c = 3 ： 5 ： 4$

查看试题解析
2. 下列图各组数中，是勾股数的是（）

A、6，8，12 B、0.6，0.8，1 C、8，15，16 D、9，12，15

查看试题解析
3. 如图，在长方体 $A B C D - E F G H$ 盒子中， $A B = 4 c m$ ， $B C = 3 c m$ ， $C G = 5 c m$ ，长为10cm的细直木棒IJ恰好从小孔G处插入，木棒的一端I与底面ABCD接触.当木棒的端点I在长方形ABCD内及边界运动时，GJ长度的最小值为（）

A、 $(10 - 5 \sqrt{2}) c m$ B、3cm C、 $(10 - 4 \sqrt{2}) c m$ D、5cm

查看试题解析
4. 在△ABC中，∠A ， ∠B ， ∠C的对边分别记为a ， b ， c ，根据以下条件：①∠A+∠B＝∠C；②a：b：c＝3：4：5；③a²＝c²﹣b²；④∠A：∠B：∠C＝1：2：3；⑤a＝3² ， b＝4² ， c＝5²； ⑥a＝ $\frac{1}{3}$ ， b＝ $\frac{1}{4}$ ， c＝ $\frac{1}{5}$ ．能判定△ABC为直角三角形的有（　　）

A、①②③⑤ B、②③④⑤ C、①②③④ D、①②③④⑤⑥

查看试题解析
5. 如图，在四边形ABCD中，∠DAB＝∠BCD＝90°，分别以四边形ABCD的四条边为边向外作四个正方形，面积分别为a，b，c，d．若a＝2，b+c＝12，则d为（　　）

A、8 B、10 C、12 D、14

查看试题解析
6. 满足a²+b²＝c²的三个正整数a、b、c，被称为勾股数．下列各组数是勾股数的是（　　）

A、7，24，25 B、3² ， 4² ， 5² C、1.5，2，2.5 D、 $\sqrt{3} ， \sqrt{4} ， \sqrt{7}$

查看试题解析
7. 现有一个圆柱体水晶杯（容器厚度忽略不计），其底面圆的周长为 $16 c m$ ，高为 $15 c m$ ，在杯子内壁离容器底部 $4.5 c m$ 的点B处有一滴蜂蜜，与蜂蜜相对，此时一只蚂蚁正好在杯子外壁，离容器上沿 $4.5 c m$ 的点A处，则蚂蚁吃到蜂蜜需爬行的最短路径为（）

A、 $17 c m$ B、 $10 c m$ C、 $2 \sqrt{73} c m$ D、 $16 c m$

查看试题解析
8. 如果正整数a、b、c满足等式 $a^{2} + b^{2} = c^{2}$ ，那么正整数a、b、c叫做勾股数．某同学将自探究勾股数的过程列成下表，观察表中每列数的规律，可知 $x + y$ 的值为（）
a
b
c
3
4
5
8
6
10
15
8
17
24
10
26
…
…
…
x
14
y

A、67 B、34 C、98 D、73

查看试题解析

二、填空题

9. 如图，在平面直角坐标系中，点 $A$ 的坐标是 $(- 3 ， 0)$ ，点 $B$ 的坐标是 $(0 ， 4)$ ，点 $C$ 是 $O B$ 上一点，将 $△ A B C$ 沿 $A C$ 折叠，点 $B$ 恰好落在 $x$ 轴上的点 $B^{'}$ 处，则点 $C$ 的坐标为．

查看试题解析
10. 如图，在高 $B C = 3 m$ ，斜坡长 $A B = 5 m$ ，宽为2m的楼梯表面铺地毯，则地毯的面积至少需要 $m^{2}$ .

查看试题解析
11. 如图，长方体的底面边长分别为 $1 c m$ 和 $3 c m$ ，高为 $6 c m$ ．如果用一根细线从点 $A$ 开始经过4个侧面缠绕1圈到达点 $B$ ，那么所用细线最短需要 $c m$ ；如果从点 $A$ 开始经过4个侧面缠绕2圈到达点 $B$ ，那么所用细线最短需要 $c m$ ．

查看试题解析
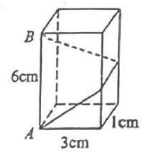12. 如图，在Rt△ABC中，∠ACB＝90°，BC=40cm，AC＝30cm ，动点P从点B出发沿射线BA以2cm/s的速度运动．则当运动时间t＝s时，△BPC为直角三角形．

查看试题解析
13. 边长分别为4cm，3cm两正方体如图放置，点P在 $E_{1} F_{1}$ 上，且 $E_{1} P = \frac{1}{3} E_{1} F_{1}$ ，一只蚂蚁如果要沿着长方体的表面从点A爬到点P，需要爬行的最短距离是cm．

查看试题解析

三、解答题

14. 如图，AO⊥OM ， OA＝4cm，点B从O点出发沿射线OM运动，速度为1cm/s，分别以OB，AB为直角边，B为直角顶点，在OM两侧作等腰Rt△OBF、等腰Rt△ABE.

(1)、当t=3s时，
①求AB的长；
②连接AF，求AF的长。

(2)、连接EF交OM于P点，当点B在射线OM上移动时，PB的长度会变化吗？若会变化，请说明理由；若不变，请求出PB的长度.

查看试题解析
15. 如图，在△ABC中，∠ACB＝90°，点E，F在边AB上，将边AC沿CE翻折，使点A落在AB上的点D处，再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，

(1)、求∠ECF的度数；

(2)、若CE＝4，B′F＝1，求线段BC的长和△ABC的面积．

查看试题解析

四、综合题

16. 定义：如图，点M ， N把线段 $A B$ 分割成 $A M ， M N ， B N$ ．若以 $A M ， M N ， B N$ 为边的三角形是一个直角三角形，则称点M ， N是线段 $A B$ 的勾股分割点．

(1)、已知点M ， N把线段 $A B$ 分割成 $A M ， M N ， B N$ ，若 $A M = 1.5$ ， $M N = 2.5$ ， $B N ＝ 2$ ，则点M ， N 是线段 $A B$ 的勾股分割点吗？请说明理由；

(2)、已知点M ， N是线段 $A B$ 的勾股分割点，且 $A M$ 为直角边，若 $A B ＝ 24 ， A M ＝ 6$ ，求 $B N$ 的长．

查看试题解析
17. 在 $△ A B C$ 中， $B C = a$ ， $A C = b$ ， $A B = c$ ，设 $c$ 为最长边，当 $a^{2} + b^{2} = c^{2}$ 时， $△ A B C$ 是直角三角形；当 $a^{2} + b^{2} \neq c^{2}$ 时，利用代数式 $a^{2} + b^{2}$ 和 $c^{2}$ 的大小关系，探究 $△ A B C$ 的形状 $($ 按角分类 $)$ ．

(1)、当 $△ A B C$ 三边分别为6、8、9时， $△ A B C$ 为三角形；当 $△ A B C$ 三边分别为6、8、11时， $△ A B C$ 为三角形．

(2)、猜想，当 $a^{2} + b^{2}$ $c^{2}$ 时， $△ A B C$ 为锐角三角形；当 $a^{2} + b^{2}$ $c^{2}$ 时， $△ A B C$ 为钝角三角形．

(3)、判断当 $a = 2$ ， $b = 4$ 时， $△ A B C$ 的形状，并求出对应的 $c$ 的取值范围．

查看试题解析

a	b	c
3	4	5
8	6	10
15	8	17
24	10	26
…	…	…
x	14	y