2023-2024学年人教版(吉林地区)初中数学八年级下册 17.2 勾股定理的逆定理同步分层训练基提升题

试卷更新日期：2024-01-26 类型：同步测试

进入出卷网下载

一、选择题

1. 已知a、b、c分别是△ABC的三边，根据下列条件能判定△ABC为直角三角形的是（）

A、a=8，b=13，c=11 B、a=6，b=10，c=12 C、a=40，b=4l，c=9 D、a=24，b=9，c=25

查看试题解析
2. 如果梯子的底端离建筑物1.5米，2.5米长的梯子可以达到建筑物的高度是（）

A、2米 B、2.5米 C、3米 D、3. 5米

查看试题解析
3. 四根小棒的长分别是5，9，12，13，从中选择三根小棒首尾相接，搭成边长如下的四个三角形，其中是直角三角形的是(　　)

A、5，9，12 B、5，12，13 C、5，9，13 D、9，12，13

查看试题解析
4. 如图，图中小正方形的边长都为1，△ABC的顶点都在格点上，则△ABC是（）

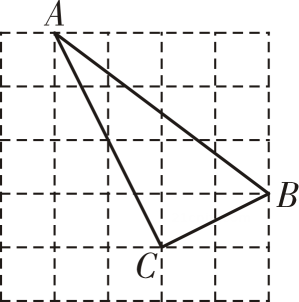A、直角三角形 B、锐角三角形 C、钝角三角形 D、无法判断

查看试题解析
5. 如图，在每个小正方形的边长都为1的方格中，A，B，C，D均为格点，构成图中三条线段AB，BC，CD现在取出这三条线段AB，BC，CD首尾相连拼三角形．下列判断中正确的是（）

A、能拼成一个直角三角形 B、能拼成一个锐角三角形 C、能拼成一个钝角三角形 D、不能拼成三角形

查看试题解析
6. 如图，一只蚂蚁绕着圆柱向上螺旋式爬行，假设蚂蚁绕圆柱外壁从点A爬到点B ，圆周率π取近似值3，则蚂蚁爬行路线的最短路径长为（　　）

A、6 $\sqrt{2}$ cm B、6 $\sqrt{5}$ cm C、2 $\sqrt{13}$ cm D、10cm

查看试题解析
7. 勾股定理又称毕达哥拉斯定理、商高定理、百牛定理，是人类早期发现并证明的重要数学定理之一、如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ，以 $R t △ A B C$ 各边为边向外作正方形 $A B F G$ 、正方形 $A C H I$ 、正方形 $B C D E$ ．连接 $G I$ 、 $E F$ 、 $D H$ ，若 $E F = \sqrt{34}$ ， $D H = 4$ ，则这个六边形 $E D H I G F$ 的面积为（）

A、28 B、26 C、32 D、30

查看试题解析

二、填空题

8. 如图，长方体的底面边长分别为 $3 c m$ 和 $3 c m$ ，高为 $5 c m$ ，如果一只蚂蚁从点 $P$ 开始经过四个侧面爬行一圈到达点 $Q$ ，那么蚂蚁爬行的最短路径长为 $c m$ ．

查看试题解析
9. 如图是一个提供床底收纳支持的气压伸缩杆，除了AB是完全固定的钢架外，AD，BC，DE属于位置可变的定长钢架.如图1所示， $A B = 29 c m ， A D = 13 c m ， B C = 20 c m$ ，伸缩杆PQ的两端分别固定在BC，CE两边上，其中 $P B = 13 c m ， C Q = 20 c m$ .当伸缩杆PQ打开最大时，如图2所示， $∠ A D C$ 成 $18 0^{°}$ ，此时 $P Q = \sqrt{449} c m$ ，则可变定长钢架CD的长度为 $c m$ .当伸缩杆完全收拢时， $C D / / A B$ ，则此时床高(CD与AB之间的距离）为cm.

查看试题解析
10. 如图一只蚂蚁从长为5cm，宽为3cm，高为4cm的长方体纸箱的A点沿纸箱爬到B点，那么它爬行的最短距离是cm．

查看试题解析
11. 在一个长为2米，宽为1米的长方形草地上，如图堆放着一根正三棱柱的木块，它的侧棱长平行且大于场地宽AD，木块的主视图是边长为0.4米的正三角形，一只蚂蚁从点A处到C处需要走的最短路程是米．

查看试题解析
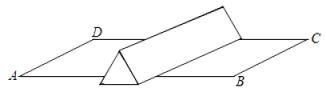12. 如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB=∠B=30°，OA=2，将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是

查看试题解析

三、解答题

13. 某小区在社区管理人员及社区居民的共同努力之下，在临街的拐角建造了一块绿化地（阴影部分）．如图，已知 $A B = 9 m ， B C = 12 m ， C D = 17 m ， A D = 8 m$ ，技术人员通过测量确定了 $∠ A B C = 90 °$ ．

(1)、小区内部分居民每天必须从点 $A$ 经过点 $B$ 再到点 $C$ 位置，为了方便居民出人，技术人员打算在绿地中开辟一条从点 $A$ 直通点 $C$ 的小路，请问如果方案落实施工完成，居民从点 $A$ 到点 $C$ 将少走多少路程？

(2)、这片绿地的面积是多少？

查看试题解析
14. 如图，在△ABC中，CD⊥AB于点D ，若CD＝12，AD＝16，BC＝15．

(1)、求AC ， BD的长；

(2)、判断△ABC的形状并说明理由．

查看试题解析

四、综合题

15. 如图，C地到A，B两地分别有笔直的道路 $C A$ ， $C B$ 相连，A地与B地之间有一条河流通过，A，B，C三地的距离如图所示.

(1)、如果A地在C地的正东方向，那么B地在C地的什么方向？

(2)、现计划把河水从河道 $A B$ 段的点D引到C地，求C，D两点间的最短距离.

查看试题解析
16. 我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、添项拆项法、十字相乘法等等．①分组分解法：将一个多项式适当分组后，可提公因式或运用公式继续分解的方法叫作分组分解法．
例如： $4 x^{2} - 4 x - y^{2} + 1 = (4 x^{2} - 4 x + 1) - y^{2} = {(2 x - 1)}^{2} - y^{2} = (2 x - y - 1) (2 x + y - 1)$

②十字相乘法：十字相乘法能用于二次三项式的分解因式．

分解步骤：1．分解二次项，所得结果分别写在十字交叉线的左上角和左下角；2．分解常数项，所得结果分别写在十字交叉线的右上角和右下角；3．交叉相乘，求代数和，使其等于一次项；4．观察得出原二次三项式的两个因式，并表示出分解结果．这种分解方法叫作十字相乘法．

例如： $x^{2} - 3 x - 40$ 分析： $x^{2} - 3 x - 40$

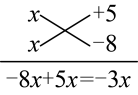
观察得出：两个因式分别为 $(x + 5)$ 与 $(x - 8)$

解：原式 $= (x + 5) (x - 8)$

③添项拆项法：将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法叫作拆项法．

例如： $y^{2} - 10 y + 21 = y^{2} - 10 y + 25 - 4 = {(y - 5)}^{2} - 2^{2} = (y - 5 + 2) (y - 5 - 2) = (y - 3) (y - 7)$ ．

(1)、仿照以上方法，按照要求分解因式：
①（分组分解法） $a b - a - b + 1 =$ ；
②（十字相乘法） $y^{2} + 3 y - 10 =$ ；

(2)、已知：a、b、c为 $△ A B C$ 的三条边， $a^{2} + b^{2} + c^{2} - 6 a = 10 b + 8 c - 50$ ，判断 $△ A B C$ 的形状．

查看试题解析