2023-2024学年人教版(吉林地区)初中数学八年级下册 17.2 勾股定理的逆定理同步分层训练基础题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 下列条件中,能判定为直角三角形的是( )A、 B、 C、:::: D、 ,2. 下列各组数分別为一个三角形三边的长,其中能构成直角三角形的一组是( )A、1,2,3 B、4,5,6 C、7,24,25 D、8,15,183. 有五根小木棒,其长度分别为7,15,20,24,25.现将它们摆成两个直角三角形,下面摆放正确的是( )A、
 B、
B、 C、
C、 D、
D、 4. 已知一组勾股数中的两个数分别是3和4,那么第三个数是gt( )A、5 B、5或 C、 D、75. 如果一个三角形的三边满足关系式 , 那么这个三角形的形状为( )A、锐角三角形 B、针角三角形 C、直角三角形 D、以上都不对6. 下列条件中,不能判定△ABC是直角三角形的是( )A、∠A=∠B+∠C B、a:b:c=5:12:13 C、a2=(b+c)(b-c) D、∠A:∠B:∠C=3:4:57. 如图,在正方形网格中,每个小正方形的边长都是1,四条线段,其中能组成直角三角形三边的一组线段是( )
4. 已知一组勾股数中的两个数分别是3和4,那么第三个数是gt( )A、5 B、5或 C、 D、75. 如果一个三角形的三边满足关系式 , 那么这个三角形的形状为( )A、锐角三角形 B、针角三角形 C、直角三角形 D、以上都不对6. 下列条件中,不能判定△ABC是直角三角形的是( )A、∠A=∠B+∠C B、a:b:c=5:12:13 C、a2=(b+c)(b-c) D、∠A:∠B:∠C=3:4:57. 如图,在正方形网格中,每个小正方形的边长都是1,四条线段,其中能组成直角三角形三边的一组线段是( ) A、 B、 C、 D、8. 如图,在△ABC中, , , 以AB,AC为边作正方形,这两个正方形的面积和为( )
A、 B、 C、 D、8. 如图,在△ABC中, , , 以AB,AC为边作正方形,这两个正方形的面积和为( )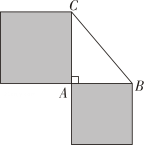 A、6 B、36 C、16 D、49
A、6 B、36 C、16 D、49二、填空题
-
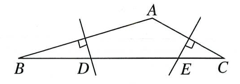
9. 如图,在△ABC中,已知∠A为钝角,边AB,AC的中垂线分别交BC于点D,E.若BD2+CE2=DE2 , 则∠A= .
 10. 如图是一台雷达探测相关目标得到的结果,若记图中目标A的位置为(2,),目标B 的位置为(4,),现有一个目标C的位置为(3,),且与目标B的距离为5,则目标C的位置为 .
10. 如图是一台雷达探测相关目标得到的结果,若记图中目标A的位置为(2,),目标B 的位置为(4,),现有一个目标C的位置为(3,),且与目标B的距离为5,则目标C的位置为 . 11. 如图,一场暴雨过后,垂直于地面的一棵树在距地面米的点处折断,树尖恰好碰到地面,经测量米,则树高为米.
11. 如图,一场暴雨过后,垂直于地面的一棵树在距地面米的点处折断,树尖恰好碰到地面,经测量米,则树高为米. 12. 在中,若 , 则 .13. 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的大意是:如图,有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个水池的深度是尺.
12. 在中,若 , 则 .13. 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的大意是:如图,有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个水池的深度是尺.
三、解答题
-
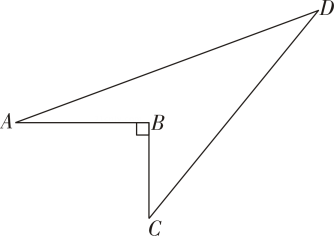
14. 在中,的对边分别用来表示,且满足 , 试判断的形状.15. 如图,一块草坪的形状为四边形 , 其中 , , , , 求这块草坪的面积.
四、综合题
-
16. 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.
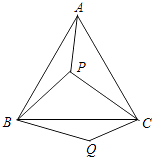 (1)、观察并猜想AP与CQ之间的大小关系,并说明理由.(2)、若PA=3,PB=4,PC=5,连结PQ,判断△PQC的形状并说明理由.17.
(1)、观察并猜想AP与CQ之间的大小关系,并说明理由.(2)、若PA=3,PB=4,PC=5,连结PQ,判断△PQC的形状并说明理由.17. (1)、如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)、如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程;(3)、若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?
(1)、如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)、如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程;(3)、若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?