人教版(吉林地区)初中数学八年级下册 17.1 勾股定理同步分层训练培优题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 如图,阴影部分是一个长方形,它的面积是( )
 A、3cm2 B、4cm2 C、5cm2 D、6cm22. 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
A、3cm2 B、4cm2 C、5cm2 D、6cm22. 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( ) A、2 B、 C、 D、3.
A、2 B、 C、 D、3.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
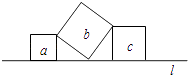 A、4 B、6 C、16 D、554. 如图,在Rt△ABC中.∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=2,则AC的长是( )
A、4 B、6 C、16 D、554. 如图,在Rt△ABC中.∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=2,则AC的长是( ) A、4 B、8 C、4 D、25. 如图,图形是由两个直角三角形和三个正方形组成,若正方形A、B的面积分别为8、20,大直角三角形一边长为6,则斜边长m为( )
A、4 B、8 C、4 D、25. 如图,图形是由两个直角三角形和三个正方形组成,若正方形A、B的面积分别为8、20,大直角三角形一边长为6,则斜边长m为( ) A、8 B、9 C、10 D、6. 如图,正方形的边长为3,以为一边作等边三角形 , 点在正方形内部,则点到的距离是( )
A、8 B、9 C、10 D、6. 如图,正方形的边长为3,以为一边作等边三角形 , 点在正方形内部,则点到的距离是( )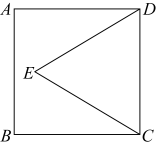 A、3 B、 C、 D、7. 如图,为等腰直角三角形, , 以斜边为直角边作等腰直角三角形 , 再以为直角边作等腰直角三角形 , , 按此规律作下去,则的长度为( )
A、3 B、 C、 D、7. 如图,为等腰直角三角形, , 以斜边为直角边作等腰直角三角形 , 再以为直角边作等腰直角三角形 , , 按此规律作下去,则的长度为( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 , , 点是轴上的一个动点.结合图形得出式子的最小值是( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 , , 点是轴上的一个动点.结合图形得出式子的最小值是( )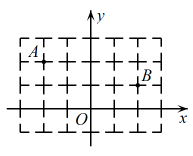 A、3 B、 C、5 D、
A、3 B、 C、5 D、二、填空题
-
9. 已知直角三角形的两边的长分别是3和4,则第三边长为 .10. 在△ABC中,AB=6,AC=5,BC边上的高AD=4,则△ABC的周长为.11. 如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高为.
 12. 若直角三角形的两直角边长为a、b,且满足 则该直角三角形的斜边长为 .13. 如图是一台多功能手机支架,图2是其侧面示意图,为地面,支架垂直地面,可分别绕点B , C转动,测量知cm,cm,cm.当转动到 , 且A , C , D三点共线时,则点A到地面的距离为cm.
12. 若直角三角形的两直角边长为a、b,且满足 则该直角三角形的斜边长为 .13. 如图是一台多功能手机支架,图2是其侧面示意图,为地面,支架垂直地面,可分别绕点B , C转动,测量知cm,cm,cm.当转动到 , 且A , C , D三点共线时,则点A到地面的距离为cm.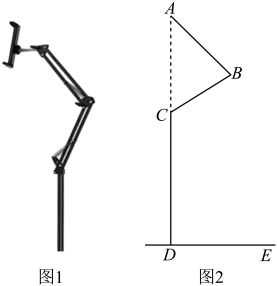
三、解答题
-
14. 如图 , 在中, , , 是的高,且 .
 (1)、求的长;(2)、若是边上的一点,作射线 , 分别过点、作于点 , 于点如图 , 若 , 求与的和.15. 用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列三个问题:
(1)、求的长;(2)、若是边上的一点,作射线 , 分别过点、作于点 , 于点如图 , 若 , 求与的和.15. 用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列三个问题: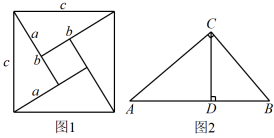 (1)、如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理 .(2)、如图2,在中,是边上的高, , 求的长度;(3)、如图1,若大正方形的面积是13,小正方形的面积是1,求的值 .
(1)、如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理 .(2)、如图2,在中,是边上的高, , 求的长度;(3)、如图1,若大正方形的面积是13,小正方形的面积是1,求的值 .四、综合题

