2023-2024学年人教版(吉林地区)初中数学八年级下册 17.1 勾股定理同步分层训练基础题
试卷更新日期：2024-01-26 类型：同步测试
一、选择题
-
1. 直角三角形的最长边的长为13，一条直角边长为5， 另一条直角边长为（ ）A、12 B、10 C、8 D、62. 如图，数轴上点A所表示的实数是（ ）
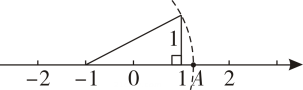A、 B、 C、 D、23. 如图，以的三边为直角边分别向外作等腰直角三角形．若 ， 则图中阴影部分的面积为（ ）
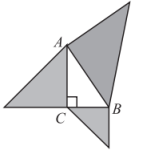A、6 B、 C、 D、254. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时， 梯子底端到左墙角的距离BC为0.7m，梯子顶端到地面的距离AC为2.4m．如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离A'D为1.5m，则小巷的宽为（ ）．
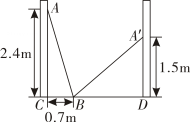A、2.4m B、2m C、2.5m D、2.7m5. 如图，是等边三角形，边长为2，根据作图的痕迹，则的长为（ ）．
A、 B、 C、 D、6. 在Rt中， ， 则点到的距离为（ ）A、 B、 C、 D、7. 如图，是一个外轮廓为长方形的机器零件平面示意图，根据图中标注的尺寸，（单位：），可得两圆孔中心和的距离是（ ）
A、 B、 C、 D、8. 如图，在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别为R、S，若AQ=PQ，PR=PS，则下列四个结论：①PA平分∠BAC；②AS=AR；③QP∥AR；④△BRP≌△CSP，其中结论正确的的序号为（ ）
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
9. 如图，方格纸中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，点C到AB边的距离为.
10. Rt△ABC中，∠ACB＝90°，AB＝13，AC＝5，则BC的长为 ．11. 如图，在数轴上点A，B对应的实数分别为1，3．BC⊥AB．BC=1．以A为圆心，AC为半径画弧，交数轴正半轴于点P，则点P对应的实数为
12. 在△ABC中，AB＝13，AC＝20，BC边上的高为12，则△ABC的面积是 ．13. 如图，在中，以A为圆心，长为半径作弧，交于C，D两点，分别以点C和点D为圆心，大于长为半径作弧，两弧交于点P，作直线 ， 交于点E，若 ， ， 则 ．
三、解答题
-
14. 已知，如图，Rt中， ， ， ， 以斜边AC为底边作等腰三角形ACD，腰AD刚好满足 ， 并作腰上的高AE．
(1)、求证：AB=AE；(2)、求等腰三角形的腰长CD．15. 在第十四届全国人大一次会议召开之际，某中学举行了庄严的升旗仪式．看着着再升起的五星红旗（如图1），小乐想用刚学过的知识计算旗杆的高度．如图2，AD为旗杆AE上用来固定国旗的绳子，点D距地面的高度 ． 将绳子AD拉至AB的位置，测得点到AE的距离 ， 到地面的垂直高度 ， 求旗杆AE的高度．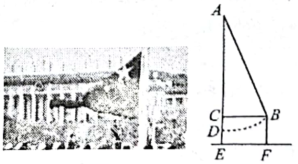
图1 图2
四、综合题
-
16. 如图，等腰直角三角板如图放置．直角顶点B在直线CD上，分别过点A、E作AC⊥直线CD于点C，ED⊥直线CD于点D．
(1)、求证：CD＝AC + ED．(2)、若设△ABC三边长分别为a、b、c，利用此图证明勾股定理．17.如图，在梯形ABCD中，AB∥DC，∠B=90°，且AB=10，BC=6，CD=2．点E从点B出发沿BC方向运动，过点E作EF∥AD交边AB于点F．将△BEF沿EF所在的直线折叠得到△GEF，直线FG、EG分别交AD于点M、N，当EG过点D时，点E即停止运动．设BE=x，△GEF与梯形ABCD的重叠部分的面积为y．
(1)、证明△AMF是等腰三角形；(2)、当EG过点D时（如图（3）），求x的值；(3)、将y表示成x的函数，并求y的最大值．