2023-2024学年人教版(吉林地区)初中数学七年级下册 6.3 实数同步分层训练培优题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 在数中,无理数是( )A、 B、0.303003 C、 D、2. 如图,数轴上,点为线段BC的中点, , 两点对应的实数分别是和 , 则点所对应的实数是( )
 A、 B、 C、 D、3. 若3-的整数部分为x , 小数部分为y , 则的值是( )A、 B、 C、 D、4. 如图,面积为6的正方形ABCD的顶点A在数轴上,且表示的数为﹣1,若点E在数轴上,(点E在点A的右侧)且AB=AE , 则点E所表示的数为( )
A、 B、 C、 D、3. 若3-的整数部分为x , 小数部分为y , 则的值是( )A、 B、 C、 D、4. 如图,面积为6的正方形ABCD的顶点A在数轴上,且表示的数为﹣1,若点E在数轴上,(点E在点A的右侧)且AB=AE , 则点E所表示的数为( )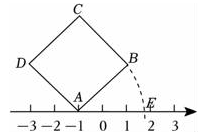 A、 B、 C、 D、5. 如图,直径为1个单位长度的圆从A点(A点在数轴上表示的数是1)沿数轴向右滚动一周后到达点B,则点B表示的数是( )
A、 B、 C、 D、5. 如图,直径为1个单位长度的圆从A点(A点在数轴上表示的数是1)沿数轴向右滚动一周后到达点B,则点B表示的数是( ) A、π B、π+1 C、π﹣1 D、2π6. 如图,A,B,C三点在数轴上所表示的数分别为a、b、c,根据图中各点位置,下列各式正确的是
A、π B、π+1 C、π﹣1 D、2π6. 如图,A,B,C三点在数轴上所表示的数分别为a、b、c,根据图中各点位置,下列各式正确的是 A、 B、 C、 D、7. 如图,半径为2个单位长度的半圆,从原点沿数轴向右滚动一周,圆上的一点由原点O到达点 , 则点所对应的数是( )
A、 B、 C、 D、7. 如图,半径为2个单位长度的半圆,从原点沿数轴向右滚动一周,圆上的一点由原点O到达点 , 则点所对应的数是( ) A、π+4 B、2π+4 C、3π D、3π+28. 如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
A、π+4 B、2π+4 C、3π D、3π+28. 如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:①abc<0;②a(b+c)>0;③a﹣c=b;④ .
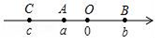
其中正确的个数有 ( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴于一点,则这个点表示的实数是
 10. 用“<”,“>”或数字填空:(1)、∵1.73231.742 ,
10. 用“<”,“>”或数字填空:(1)、∵1.73231.742 ,∴1.731.74,
∴≈(精确到0.1).
(2)、∵2.449262.4502 ,∴2.4492.450,
∴≈(精确到0.01).
11. 如图,在数轴上竖直摆放一个直径为4个单位长度的半圆,是半圆上的中点,半圆直径的一个端点位于原点. 该半圆沿数轴从原点开始向右无滑动滚动,当点第一次落在数轴上时,此时点表示的数为.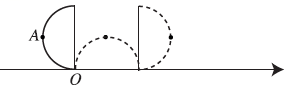 12. 如图,点 , 在数轴上,点为原点,按如图所示方法用圆规在数轴上截取 , 若点表示的数是 , 则点表示的数是 .
12. 如图,点 , 在数轴上,点为原点,按如图所示方法用圆规在数轴上截取 , 若点表示的数是 , 则点表示的数是 . 13. 阅读下列材料:因为 , 即 , 所以的整数部分为 , 小数部分为 , 若规定实数的整数部分记为 , 小数部分记为 , 可得 , 按照此规定计的值是 .
13. 阅读下列材料:因为 , 即 , 所以的整数部分为 , 小数部分为 , 若规定实数的整数部分记为 , 小数部分记为 , 可得 , 按照此规定计的值是 .三、解答题
-
14. 阅读下面的文字,解答问题.
无理数是无限不循环小数,因此无理数的小数部分我们不可能全部地写出来,比如π、等,而常用“……”或者“≈”的表示方法都不够百分百准确,于是小刚用来表示的小数部分,你同意小刚的表示方法吗?事实上,小刚的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分,又例如:因为 , 即2<<3,所以的整数部分为2,小数部分为 , 也就是说,任何一个无理数,都可以夹在两个相邻的整数之间。根据上述信息,请回答下列问题:
(1)、的整数部分是 , 小数部分是;(2)、10+也是夹在两个整数之间的,可以表示为 , 则;(3)、若 , 其中是整数,且0<y<1,求:的相反数.15. 如图,在4×4的小正方形组成的图形中有一个阴影部分(阴影部分也是正方形).若每个小正方形的边长为1,点A表示的数为1. (1)、图中正方形ABCD的面积为多少?它的边长为多少?这个值在哪两个连续整数之间?(2)、若阴影正方形的边长的值的整数部分为x,小数部分为y,求(y-)x的值.(3)、若正方形ABCD从当前状态沿数轴正方向翻滚,我们把点B翻滚到与数轴上的点P重合时,记为第一次翻滚,如图所示,C翻滚到数轴上时,记为第二次翻滚,以此类推,请直接回答:
(1)、图中正方形ABCD的面积为多少?它的边长为多少?这个值在哪两个连续整数之间?(2)、若阴影正方形的边长的值的整数部分为x,小数部分为y,求(y-)x的值.(3)、若正方形ABCD从当前状态沿数轴正方向翻滚,我们把点B翻滚到与数轴上的点P重合时,记为第一次翻滚,如图所示,C翻滚到数轴上时,记为第二次翻滚,以此类推,请直接回答:①点P表示的数为多少?
②是否存在正整数n,使得该正方形n次翻滚后,其顶点A,B,C,D中的某个点与2023重合?
四、综合题
