2023-2024学年人教版(吉林地区)初中数学七年级下册 5.3.1 平行线的性质 同步分层训练培优题
试卷更新日期：2024-01-26 类型：同步测试
一、选择题
-
1. 生活中常见的探照灯、汽车大灯等灯具都与抛物线有关。如图，从光源P点照射到抛物线上的光线PA，PB等反射以后沿着与直线PF平行的方向射出，若∠CAP=α，∠DBP=β，则∠APB的度数为（ ）
A、2α B、2β C、α+β D、(α+β)2. 一把直尺与一块直角三角板按如图方式摆放，若∠1=46°，则∠2=（ ）
A、46° B、44° C、42° D、40°3. 如图，将三角形纸片ABC沿虚线剪掉两角得五边形CDEFG，若 ， ， 根据所标数据，则的度数为（ ）
A、54° B、64° C、66° D、72°4. 如图，直线a、b被直线c所截，下列说法正确的是（ ）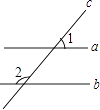
A、当∠1=∠2时，一定有a∥b B、当a∥b时，一定有∠1=∠2 C、当a∥b时，一定有∠1+∠2=90° D、当∠1+∠2=180°时，一定有a∥b5. 如图，直线AB∥CD，直线EF分别与AB， ，CD交于点E， F，EG平分∠BEF，交CD于点G， 若∠1=55°， 则∠2的度数为（ ）
A、117.5° B、110° C、118.5° D、125°6. 如图是小明探索直线平行的条件时所用的学具，木条 ， ， 在同一平面内，经测量，要使木条 ， ， 要使木条与平行，则的度数应为（ ）
A、 B、 C、 D、7. 如图， ， 将一副直角三角板作如下摆放， ， ． 下列结论：①；②；③；④ ． 其中正确的个数是（ ）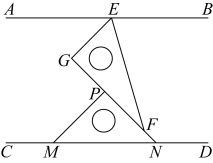
A、1 B、2 C、3 D、48. 如图，将一副直角三角尺的其中两个顶点重合叠放．其中含角的三角尺固定不动，将含角的三角尺绕顶点B顺时针转动（转动角度小于）．当与三角尺的其中一条边所在的直线互相平行时，的度数是（ ）
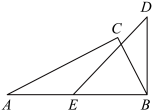A、或或 B、或或 C、或或 D、或或二、填空题
-
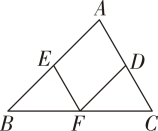
9. 如图，在三角形ABC中，D，E，F分别是三条边上的点，EF∥AC，DF∥AB，∠B=45°，∠C=60°，则∠EFD的度数为.
10. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D、C分别在M、N的位置上，若∠EFG=49°，则∠2﹣∠1= ．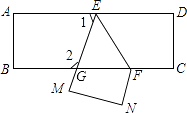
11. 如图，直线PQ∥MN，将一个有30°角的三角尺按如图所示的方式摆放，若∠CBA=43°，则∠PAC的大小为 度．
12. 如图，已知直线被直线所截， ， 点是平面内位于直线右侧的一动点（点不在直线上），设 ， 在点运动过程中，的度数可能是 ． （结果用含的式子表示）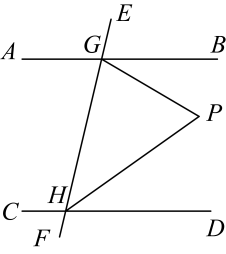
13. 如图
(1)、如图一， ， ， ， 则 ．(2)、如图二， ， ， ， ， 分别平分和 ， 则 ， 满足的数量关系为 ．三、解答题
-
14. 如图，AB∥CD，BO与CD相交于点O，OE⊥BO，OF平分∠BOD．若∠ABO=50°，求∠EOF的度数．
15. 如图，若AB∥CD，且∠1=∠2，试判断AM与CN的位置关系，并说明理由．
四、综合题
-
16. 如图，已知 ， 直线交于点 ， 交于点点是线段上一点， ， 分别在射线 ， 上，连接 ， ， 平分 ， 平分 ．
(1)、如图 ， 若 ， ， 则 ， ；(2)、如图 ， 求与之间的数量关系，并说明理由；(3)、如图 ， 当时，若 ， ， 过点作交的延长线于点将直线绕点顺时针旋转，速度为每秒 ， 直线旋转后的对应直线为 ， 同时绕点逆时针旋转，速度为每秒 ， 旋转后的对应三角形为 ， 当直线首次落到上时，整个运动停止在此运动过程中，经过秒后，直线恰好平行于的一条边，请直接写出所有满足条件的的值．17. 如图1， ， 直线与、相交于点、 ， 平分 ， 平分 ．
(1)、求证：；(2)、如图2，为、之间一点（），若 ， 求的度数；(3)、若为直线下方一点， ， 为直线右侧一点，满足 ， 则、、之间满足的数量关系是 ．