2023-2024学年人教版(吉林地区)初中数学七年级下册 5.3.1 平行线的性质 同步分层训练提升题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 如图,已知AB∥CD,则图中与∠1相等的角有( )
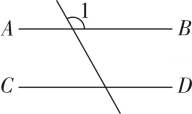 A、5个 B、4个 C、3个 D、2个2. 如图,已知∠1=70°,CD∥BE,则∠B的度数为( )
A、5个 B、4个 C、3个 D、2个2. 如图,已知∠1=70°,CD∥BE,则∠B的度数为( )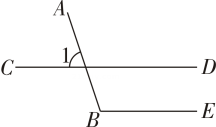 A、70° B、100° C、110° D、120°3. 如图,∠ACD是△ABC的外角,CE∥AB,若∠ACB=75°,∠ECD=50°,则∠A的度数为( )
A、70° B、100° C、110° D、120°3. 如图,∠ACD是△ABC的外角,CE∥AB,若∠ACB=75°,∠ECD=50°,则∠A的度数为( )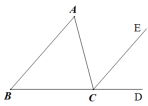 A、50° B、55° C、70° D、75°4. 如图,下列结论不正确的是( )
A、50° B、55° C、70° D、75°4. 如图,下列结论不正确的是( ) A、若∠2=∠C , 则AE∥CD B、若AD∥BC , 则∠1=∠B C、若AE∥CD , 则∠1+∠3=180° D、若∠1=∠2,则AD∥BC5. 如图,下列推理中正确的是( )
A、若∠2=∠C , 则AE∥CD B、若AD∥BC , 则∠1=∠B C、若AE∥CD , 则∠1+∠3=180° D、若∠1=∠2,则AD∥BC5. 如图,下列推理中正确的是( ) A、 , B、 , C、 , D、 ,6. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )
A、 , B、 , C、 , D、 ,6. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )已知:如图, , , 垂足为D , F , .
求证: .
证明:∵ , ,
∴ ◎ ,
∴(同位角相等,两直线平行),
∴ @ (两直线平行,同旁内角互补).
又∵ ,
∴ ▲ (同角的补角相等),
∴( ※ 相等,两直线平行).
 A、◎代表 B、@代表 C、▲代表 D、※代表同位角7. 如图:一块直角三角板的角的顶点与直角顶点分别在两平行线、上,斜边平分 , 交直线于点 , 则的大小为( )
A、◎代表 B、@代表 C、▲代表 D、※代表同位角7. 如图:一块直角三角板的角的顶点与直角顶点分别在两平行线、上,斜边平分 , 交直线于点 , 则的大小为( ) A、 B、 C、 D、8. 将一副三角板如图放置,则下列结论中,正确的是( )
A、 B、 C、 D、8. 将一副三角板如图放置,则下列结论中,正确的是( )①;②如果 , 则有;③如果 , 则有;④如果 , 则有 .
 A、①②③④ B、③④ C、①②④ D、①②③
A、①②③④ B、③④ C、①②④ D、①②③二、填空题
-
9. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若 , 则的度数是 .
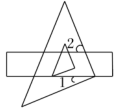 10. 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=22°,那么∠2的度数为 .
10. 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=22°,那么∠2的度数为 . 11. 一大门的栏杆如图,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
11. 一大门的栏杆如图,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= . 12. 如图,将三角板与两边平行的直尺(EF∥HG)贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=55°,则∠1的度数等于 .
12. 如图,将三角板与两边平行的直尺(EF∥HG)贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=55°,则∠1的度数等于 . 13. 如图, , 在的两边上分别过点A和点C向同方向作射线和 , 且 , 若和的角平分线所在的直线交于点P(P与C不重合),则的大小为 .
13. 如图, , 在的两边上分别过点A和点C向同方向作射线和 , 且 , 若和的角平分线所在的直线交于点P(P与C不重合),则的大小为 .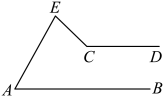
三、解答题
-
14. 如图,AB∥CD,CB平分∠ACD,∠A=50°,求∠B的度数.
 15. 如图,已知∠EPM=∠FQM.∠AEP=∠CFQ.试说明AB∥CD的理由.
15. 如图,已知∠EPM=∠FQM.∠AEP=∠CFQ.试说明AB∥CD的理由.
四、综合题
-
16. 如图,已知∠A=∠C,AD⊥BE,BC⊥BE,点E,D,C在同一条直线上.
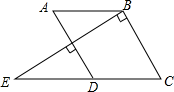 (1)、判断AB与CD的位置关系,并说明理由.(2)、若∠ABC=120°,求∠BEC的度数.17. 已知:点C是∠AOB的OA边上一点(点C不与点O重合),点D是∠AOB内部一点,射线CD不与OB相交.
(1)、判断AB与CD的位置关系,并说明理由.(2)、若∠ABC=120°,求∠BEC的度数.17. 已知:点C是∠AOB的OA边上一点(点C不与点O重合),点D是∠AOB内部一点,射线CD不与OB相交.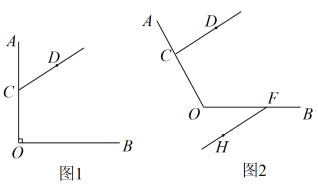 (1)、如图1,∠AOB=90°,∠OCD=120°,过点O作射线OE,使得OE//CD.(其中点E在∠AOB内部).
(1)、如图1,∠AOB=90°,∠OCD=120°,过点O作射线OE,使得OE//CD.(其中点E在∠AOB内部).①依据题意,补全图1;
②直接写出∠BOE的度数.
(2)、如图2,点F是射线OB上一点,且点F不与点O重合,当时,过点F作射线FH,使得FH//CD(其中点H在∠AOB的外部),用含的代数式表示∠OCD与∠BFH的数量关系,并证明.