2023-2024学年人教版(吉林地区)初中数学七年级下册 5.3.1 平行线的性质 同步分层训练基础题
试卷更新日期：2024-01-26 类型：同步测试
一、选择题
-
1. 如图，已知直线a∥b，∠1＝105° ，则∠2等于 （ ）
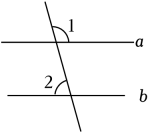A、65° B、75° C、85° D、105°2. 如图，直线 ， 被直线所截， ， ， 则的度数为（ ）
A、 B、 C、 D、3. 已知直线 m∥n．将一把含30°角的三角尺ABC按如图所示的方式放置(∠ABC=30°)，其中A、B两点分别落在直线m、n上．若∠1=20°，则∠2的度数为（ ）
A、10° B、20° C、30° D、40°4. 如果两条直线被第三条直线所截，那么（ ）A、同位角相等 B、内错角相等 C、同旁内角互补 D、对顶角相等5. 如图，直线a∥b，Rt△ABC的直角顶点A落在直线a上，点B落在直线b上，若∠1＝15°，∠2＝25°，则∠ABC的大小为（ ）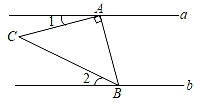
A、40° B、45° C、50° D、55°6. 如图，直线 ， 是直角三角形， ， 点C在直线n上．若 ， 则的度数是（ ）
A、60° B、50° C、45° D、40°7. 如图，快艇从P处向正北航行到A处时，向左转50°航行到B处，再向右转80°继续航行，此时的航行方向为（ ）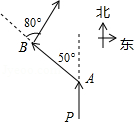
A、北偏东30° B、北偏东80° C、北偏西30° D、北偏西50°8. 如图，已知AB∥EF．若∠C=90°，则∠α，∠β，∠γ之间的关系是（ ）
A、∠β=∠α+∠γ B、∠α+∠β+∠γ=180° C、∠α+∠β-∠γ=90° D、∠β+∠γ-∠α=90°二、填空题
-
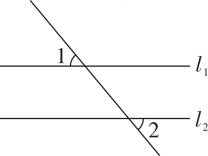
9. 如图，直线l1∥l2 ． 若∠1=52°，则∠2的度数为
10. 如图，已知AB∥CD，∠2：∠3=1：2，则∠1=°．
11. 如图，直线AB∥CD，BC平分∠ABD，∠1=65°，则∠2=.
12. 如图，若∠1+∠2=240°，b∥c，则∠3=.
13. 如图1，当光线在空气进入水中时，会发生折射，满足入射角∠1与折射角∠2的度数比为4：3，如图2，在同一平面上，两条光线同时从空气进入水中，两条入射光线与水平面夹角度数分别为x ， y ， 在水中两条折射光线的夹角度数为m、则m＝ ． （用含x ， y的式子表示）
三、解答题
-
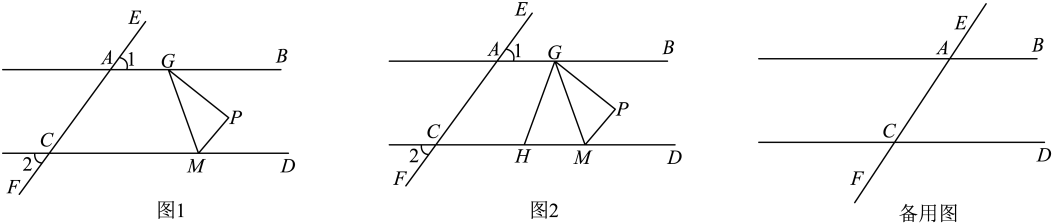
14. 如图，已知∠1=∠2=∠A．
(1)、试说明∠1=∠3的理由．(2)、当∠ADG=80°时，求∠2的度数．15. 如图①．在四边形ABCD中．∠ABC+∠ADC=180°，BE、DF分别是∠ABC与∠ADC的平分线，∠ADF与∠AFD互余．
(1)、试判断直线BE与DF的位置关系．并说明理由．(2)、如图②，延长CB、DF相交于点G，过点B作BH⊥FG，垂足为H．试判断∠FBH与∠GBH的大小关系，并说明理由．四、综合题
