2023-2024学年人教版(吉林地区)初中数学七年级下册 5.2.2 平行线的判定 同步分层训练培优题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 如图,能判断的条件是( )
 A、 B、 C、 D、2. 如图,能判定的是( )
A、 B、 C、 D、2. 如图,能判定的是( )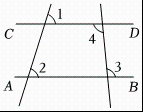 A、 B、 C、 D、3. 如图,给出下列条件.①;②;③ , 且;④其中,能推出的条作为( )
A、 B、 C、 D、3. 如图,给出下列条件.①;②;③ , 且;④其中,能推出的条作为( )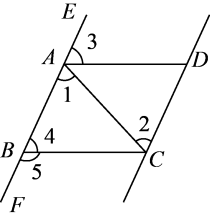 A、①②③ B、①②④ C、①③④ D、②③④4. 如图,点E在的延长线上,下列条件中能判断的是( )
A、①②③ B、①②④ C、①③④ D、②③④4. 如图,点E在的延长线上,下列条件中能判断的是( ) A、 B、 C、 D、5. 如图,下列条件中:(1);(2);(3);(4) . 能判定的条件个数有( )
A、 B、 C、 D、5. 如图,下列条件中:(1);(2);(3);(4) . 能判定的条件个数有( )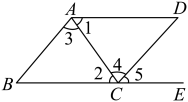 A、1个 B、2个 C、3个 D、4个6. 如图,由下列条件不能得到的是( )
A、1个 B、2个 C、3个 D、4个6. 如图,由下列条件不能得到的是( ) A、 B、 C、 D、7. 一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )
A、 B、 C、 D、7. 一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )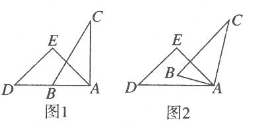 A、 和 B、 和 C、 和 D、以上都有可能8. 如下图,在下列条件中,能判定AB//CD的是( )
A、 和 B、 和 C、 和 D、以上都有可能8. 如下图,在下列条件中,能判定AB//CD的是( )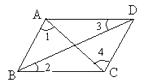 A、∠1=∠3 B、∠2=∠3 C、∠1=∠4 D、∠3=∠4
A、∠1=∠3 B、∠2=∠3 C、∠1=∠4 D、∠3=∠4二、填空题
-
9. 如图,在四边形ABCD中,点E是AB延长线上一点,请添加一个条件,使AB//CD,那么可以添加的条件是(写出一个即可).
 10. 如图,若 , 则当度时, .
10. 如图,若 , 则当度时, . 11. 如图,写出一个能判定的条件 .
11. 如图,写出一个能判定的条件 . 12. 在间一平面内,有2019条互不重合的直线,l1 , l2 , l3 , …,l2019 , 若l1⊥l2 , l2∥l3 , l3⊥l4 , l4∥l5 , 以此类推,则l1和l2019的位置关系是.13.
12. 在间一平面内,有2019条互不重合的直线,l1 , l2 , l3 , …,l2019 , 若l1⊥l2 , l2∥l3 , l3⊥l4 , l4∥l5 , 以此类推,则l1和l2019的位置关系是.13.已知:如图,∠1=∠2,求证:AB∥CD
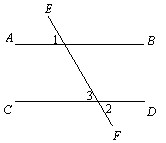
∵ ∠1=∠2,(已知)
又∠3=∠2,
∴∠1= .
∴ AB∥CD.( , )
三、解答题
-
14. 一副三角尺按如图1的方式叠放,现将含45°角的三角尺ADE固定不动,把含30°角的三角尺ABC绕顶点A顺时针旋转∠α(∠α=∠BAD且0°<∠α<180°),使两块三角尺至少有一组边平行.
 (1)、如图2,α=度时,BC∥DE.(2)、请分别在图3、图4内画一种符合要求的图形,标出α,并完成各项填空:
(1)、如图2,α=度时,BC∥DE.(2)、请分别在图3、图4内画一种符合要求的图形,标出α,并完成各项填空:①图3中,当α=度时,∥ .
②图4中,当α=度时,∥ .
15. 已知:如图, , , , , 求证: .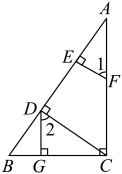
证明:∵ , (已知)
∴ , (垂直定义)
∴
∴( )
∴ ▲ ( )
∵(已知)
∴ ▲ (等量代换)
∴( )
∴ ▲ ( )
∵(已知)
∴(垂直定义)
∴ ▲ (等量代换)
∴(垂直定义)
四、综合题
-
16. 如图,已知点O在直线AB上,射线OE平分∠AOC,过点O作OD⊥OE,G是射线OB上一点,连接DG,使∠ODG+∠DOG=90°.
 (1)、求证:∠AOE=∠ODG;(2)、若∠ODG=∠C,试判断CD与OE的位置关系,并说明理由.17. 三角板是学习数学的重要工具 ,将一副三角板的直角顶点 C 按如图所示的方式叠放在一起, 当 时 ,且点 E 在直线AC 的上方时, 解决下列问题∶ (友情提示 ∶ ∠A=60°,∠D=30°,∠B=∠E=45°)
(1)、求证:∠AOE=∠ODG;(2)、若∠ODG=∠C,试判断CD与OE的位置关系,并说明理由.17. 三角板是学习数学的重要工具 ,将一副三角板的直角顶点 C 按如图所示的方式叠放在一起, 当 时 ,且点 E 在直线AC 的上方时, 解决下列问题∶ (友情提示 ∶ ∠A=60°,∠D=30°,∠B=∠E=45°) (1)、①若 ∠DCE=45°,求∠ACB;
(1)、①若 ∠DCE=45°,求∠ACB;②若∠ACB=140°,求∠DCE ;
(2)、由(1)猜想 ∠ACB与∠DCE的数量关系,并说明理由;(3)、这两块三角板是否存在一组边互相平行?若存在,请直接写出∠ACE的所有可能的值(不必说明理由);若不存在,请说明理由.