2023-2024学年人教版(吉林地区)初中数学七年级下册 5.2.2 平行线的判定 同步分层训练提升题
试卷更新日期：2024-01-26 类型：同步测试
一、选择题
-
1. 如图所示，下列推理中，正确的是（ ）
A、∵∠A+∠D=180°，∴AD∥BC B、∵∠C+∠D=180°，∴AB∥CD C、∵∠A+∠D=180°，∴AB∥CD D、∵∠A+∠C=180°，∴AB∥CD2. 下列条件中不能判定AB∥CD的是( )
A、∠1＝∠4 B、∠2＝∠3 C、∠5＝∠B D、∠BAD+∠D＝180°3.如图，点E在CD延长线上，下列条件中不能判定AB∥CD的是（ ）
A、∠1＝∠2 B、∠3＝∠4 C、∠5＝∠B D、∠B+∠BDC＝180°4. 如图所示为一张四边形纸片ABCD，下列测量方法中，能判定AD∥BC的是（ ）
A、AB⊥BC，CD⊥BC B、AB⊥BC，AB⊥AD C、AB⊥BC，CD⊥AD D、AB=DC5. 木条a、b、c如图用螺丝固定在木板上，且∠ABM=50°，∠DEM=70°，将木条a、b、c看作是在同一平面内的三条直线AC、DF、MN若使直线AC、DF达到平行的位置关系，则下列描述错误的是（ ）
A、木条b、c固定不动，木条a绕点B顺时针旋转20° B、木条b、c固定不动，木条a绕点B逆时针旋转160° C、木条a、c固定不动，木条b绕点E逆时针旋转20° D、木条a、c固定不动，木条b绕点E顺时针旋转110°6. 如图，下列条件中，能判定的是（ ）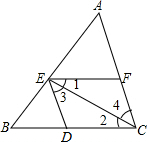
A、 B、 C、 D、7.如图，经过直线a外一点O的4条直线中，与直线a相交的直线至少有（ ）
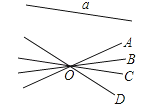A、4条 B、3条 C、2条 D、1条8. 一副三角板按如图所示叠放在一起，其中点、重合，若固定三龟板 ， 三角板绕点在平面内旋转，当（ ）时， ．
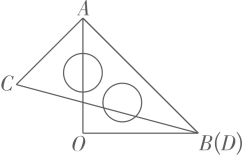A、 B、或 C、或 D、或二、填空题
-
9. 如图，若∠B=65°，∠C=15°，∠E=50°，∠DFE=∠E+∠C，则AB与CD的位置关系是.
10. 如图，不添加辅助线，请写出一个能判定的条件 ．
11. 如图，现给出下列条件：①∠1=∠B，②∠2=∠5，③∠3=∠4，④∠BCD+∠D=180°．其中能够得到AB∥CD的条件有 ． （填序号）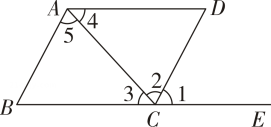
12. 如图，现给出下列条件：①∠1=∠B，②∠2=∠5，③∠3=∠4，④∠BCD+∠D=180°．其中能够得到AB∥CD的条件有 ． （填序号）13. 一副直角三角尺如图①叠放，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动，要求两块三角尺的一组边互相平行.如图②，当∠BAD=15°时，有一组边BC∥DE，请再写出两个符合要求的∠BAD（0°＜∠BAD＜180°）的度数.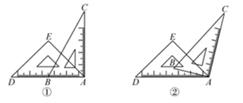
三、解答题
-
14. 如图，∠B=∠C，点B、A、E在同一条直线上，∠EAC=∠B+∠C，且AD平分∠EAC，试说明AD∥BC的理由
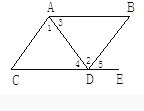
15. 如图，已知AC⊥BC，∠1与∠2互余，根据已知条件，你能判定哪两条直线平行？请说明理由．
四、综合题
