2023-2024学年人教版(吉林地区)初中数学七年级下册 5.1.3 同位角、内错角、同旁内角 同步分层训练培优题

试卷更新日期：2024-01-26 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 下列图形中，∠1和∠2为同旁内角的是（ ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 如图，AB∥CD，点E在BC上，DE⊥BC，∠B=40°，则∠D的度数为（ ）

    A、40° B、50° C、38° D、60°

    查看试题解析

  • 3. 下列说法正确的是（ ）
    A、相等的角是对顶角 B、两个锐角的和是锐角 C、邻补角互补 D、同旁内角互补

    查看试题解析

  • 4.

    如图，直线a，b被直线c所截，则下列说法中错误的是（　　）

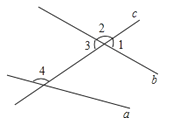    A、∠1与∠2是邻补角 B、∠1与∠3是对顶角 C、∠2与∠4是同位角 D、∠3与∠4是内错角

    查看试题解析

  • 5. 如图，直线a、b被c所截，下列说法中错误的是（  ）

    A、∠1的对顶角是47° B、∠1的内错角是47° C、∠1的同旁内角是133° D、∠1的同位角是47°

    查看试题解析

  • 6. 如图，直线a，b被c所截，则∠1与∠2是（  ）

    A、同位角 B、内错角 C、同旁内角 D、邻补角

    查看试题解析

  • 7. 如图，下列6种说法：①∠1与∠4是内错角；②∠1与∠2是同位角；③∠2与∠4是内错角；④∠4与∠5是同旁内角；⑤∠2与∠4是同位角；⑥∠2与∠5是内错角．其中正确的有 (     )

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 8. 如图所示，与∠α构成同位角的角的个数为(　 　)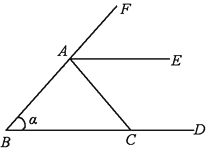

    A、1 B、2 C、3 D、4

    查看试题解析

二、填空题

  • 9. 如图，AB∥CD ， EF⊥AB于点E，EF交CD于点F ， 已知∠1=20°18' ， 则∠2的度数为 ．

    查看试题解析

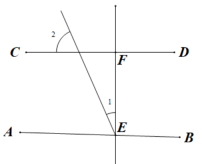  • 10. 如图，有下列3个结论：①能与∠DEF构成内错角的角的个数是2；②能与∠EFB构成同位角的角的个数是1；③能与∠C构成同旁内角的角的个数是4，以上结论正确的是.

    查看试题解析

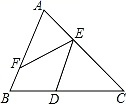  • 11. 如图，直线a∥b，∠1=120°，则∠2的度数为 ．

    查看试题解析

  • 12. 如图，直线 AB、CD 被直线  EF 所截， ∠A 和是同位角， ∠A 和是内错角

    查看试题解析

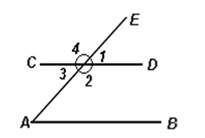  • 13. n条水平直线与倾斜直线a相交可得条线段，对同位角，对内错角，对同旁内角．

    查看试题解析

三、解答题

  • 14. 图中的∠1与∠C、∠2与∠B、∠3与∠C，各是哪两条直线被哪一条直线所截形成的同位角？

    查看试题解析

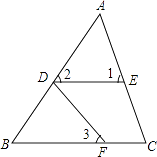  • 15. 如图，BCD是一条直线，∠1=∠B，∠2=∠A，指出∠1的同位角，∠2的内错角，并求出∠A+∠B+∠ACB的度数．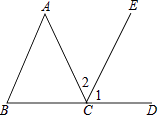

    查看试题解析

四、综合题

  • 16. 已知：如图是一个跳棋棋盘，其游戏规则是一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上例如：从起始位置∠1跳到终点位置∠3有两种不同路径，路径1：∠1→同旁内角∠9→内错角∠3；路径2：∠1→内错角∠12→内错角∠6→同位角∠10→同旁内角∠3.

    试一试：

    (1)、写出从起始位置∠1跳到终点位置∠8的一种路径；
    (2)、从起始位置∠1依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点位置∠8？

    查看试题解析

  • 17. 复杂的数学问题我们常会把它分解为基本问题来研究，化繁为简，化整为零这是一种常见的数学解题思想．

    (1)、如图1，直线 l1 ， l2 被直线 l3 所截，在这个基本图形中，形成了对同旁内角．
    (2)、如图2，平面内三条直线 l1 ， l2 ， l3 两两相交，交点分别为A、B、C，图中一共有对同旁内角．
    (3)、平面内四条直线两两相交，最多可以形成对同旁内角．
    (4)、平面内n条直线两两相交，最多可以形成对同旁内角．

    查看试题解析