2023-2024学年人教版(吉林地区)初中数学七年级下册 5.1.2 垂线 同步分层训练提升题
试卷更新日期：2024-01-26 类型：同步测试
一、选择题
-
1. 下列生活、生产现象中，可以用基本事实“两点之间线段最短”来解释的是（ ）A、用两个钉子就可以把木条固定在墙上 B、植树时只要确定两个坑的位置，就能确定同一行的树坑所在的直线 C、如果把A，B两地间弯曲的河道改直，那么就能缩短原来河道的长度 D、测量运动员的跳远成绩时，皮尺与起跳线保持垂直2. 下列选项中，过点P画AB的垂线CD，三角板放法正确的是（ ）
A、A B、B C、C D、D3. 小明在做一道数学题．直线AB，CD相交于点O，∠BOC＝25°，过点O作 ，求∠AOE的度数．小明得到 ，但老师说他少了一个答案．那么∠AOE的另一个值是（ ）A、105° B、115° C、125° D、135°4. 如图， ， 点A到直线的距离为3，若在射线上只存在一个点 ， 记的长度为 ， 则的值可以是（ ）
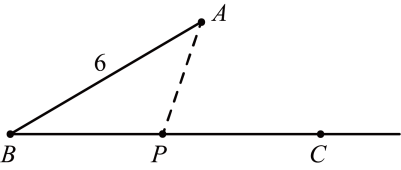A、7 B、2 C、5 D、65. 下列利用三角板过点P画直线的垂线 ， 正确的是（ ）A、
B、
C、
D、
6. 如图，在三角形ABC中，∠C=90°，AC=5，点P是BC边上的动点，则AP的长不可能是（ ）
A、4.5 B、5 C、6 D、77. 如图，直线公路l上共有A、B、C、D四个核酸检测点，若从点M用相同速度到任意一个核酸检测点，用时最短的路径是（ ）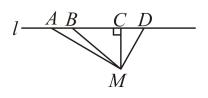
A、 B、 C、 D、8. 如图所示，∠BAC=90°，AD⊥BC，则下列结论中，正确的个数为（ ）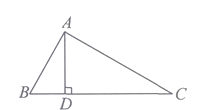
①AB⊥AC； ②AD与AC互相垂直； ③点C到AB的垂线段是线段AB；
④点A到BC的距离是线段AD的长度； ⑤线段AB的长度是点B到AC的距离；
⑥AD+BD>AB．
A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 直线AB与直线CD相交于点 ， ， 射线 ， 则的度数为.10. 如图，计划把河水l引到水池A中，先作AB⊥l ， 垂足为B ， 然后沿AB开渠，能使所开的渠道最短，这样设计的依据是： ．
11. 如图，斑马线的作用是为了引导行人安全地通过马路．小丽觉得行人沿垂直马路的方向过斑马线更为合理，这一想法体现的数学依据是 ．
12. 如图，点O在直线上，过点O作射线 ， ， ． 从下面的四个条件中任选两个，可以推出的是（写出一组满足题意的序号）．①；②和互余；③；④ ．
13. 如图，在平面内，两条直线l1 ， l2相交于点O，对于平面内任意一点M，若p，q分别是点M到直线l1 ， l2 ， 的距离，则称（p，q）为点M的“距离坐标”．根据上述规定，“距离坐标”是（3，2）的点共有个．
三、解答题
-
14. 如图，在正方形纸片的四角各剪去一个边长相等的小正方形，然后折成一个无盖的长方体盒子．一只蚂蚁要从长方体盒子的顶点A爬到顶点B，在下面左边的图中画出它爬行的最短路线，并说明理由．
15. 如图，直线AE与CD相交于点B，∠DBE=60°，BF⊥AE．求∠CBF和∠FBD的度数．
四、综合题
