2023-2024学年人教版(吉林地区)初中数学七年级下册 5.1.1 相交线 同步分层训练培优题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 如图所示,直线 , 相交于点 , 于点 , 且 , 则的度数是( )
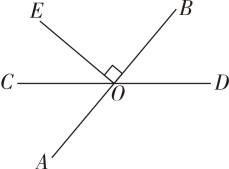 A、 B、 C、 D、2. 如图,请你观察,最接近( )
A、 B、 C、 D、2. 如图,请你观察,最接近( )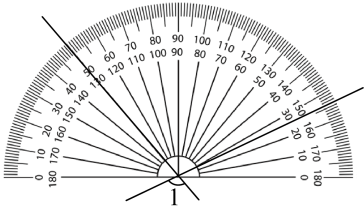 A、 B、 C、 D、3. 如图,直线a,b相交, , 则的度数为( )
A、 B、 C、 D、3. 如图,直线a,b相交, , 则的度数为( ) A、 B、 C、 D、4. 如图,若相交于点O , 过点O作 , 则下列结论不正确的是( )
A、 B、 C、 D、4. 如图,若相交于点O , 过点O作 , 则下列结论不正确的是( ) A、与互为余角 B、与互为余角 C、与是对顶角 D、与是邻补角5. 已知:如图, , 垂足为 , 为过点的一条直线,则与的关系一定成立的是( )
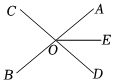
A、与互为余角 B、与互为余角 C、与是对顶角 D、与是邻补角5. 已知:如图, , 垂足为 , 为过点的一条直线,则与的关系一定成立的是( ) A、相等 B、互余 C、互补 D、互为对顶角6. 如图图形中∠1与∠2是对顶角的是( )A、
A、相等 B、互余 C、互补 D、互为对顶角6. 如图图形中∠1与∠2是对顶角的是( )A、 B、
B、 C、
C、 D、
D、 7. 用一个平面去截一个正方体所得的截面的边数最多是( )A、4 B、3 C、6 D、58. 下列语句正确的是( )A、相等的角是对顶角 B、不是对顶角的角都不相等. C、不相等的角一定不是对顶角 D、有公共点且和为180°的两个角是对顶角.
7. 用一个平面去截一个正方体所得的截面的边数最多是( )A、4 B、3 C、6 D、58. 下列语句正确的是( )A、相等的角是对顶角 B、不是对顶角的角都不相等. C、不相等的角一定不是对顶角 D、有公共点且和为180°的两个角是对顶角.二、填空题
-
9. 两条直线相交所成的四个角中,有两个角分别是和 , 则 .10. 如图,直线、相交于点 , 平分 , 若 , 则的度数是 .
 11. 如图,直线 , 相交于点O, , 垂足为O.若 , 则的度数为 .
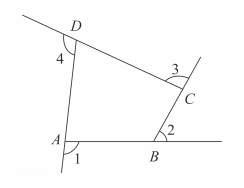
11. 如图,直线 , 相交于点O, , 垂足为O.若 , 则的度数为 . 12. 如图是由射线、、、组成的平面图形,则°.
12. 如图是由射线、、、组成的平面图形,则°.
 13. 如图,直线相交于点O,射线平分 , 若 , 则等于 .
13. 如图,直线相交于点O,射线平分 , 若 , 则等于 .
三、解答题
-
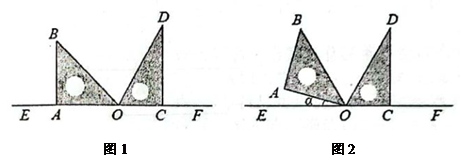
14. 一制三角板按图1方式拼接在一起 , 其中边OA , OC与直线EF重合, , 保持三角板COD不动,将三角板AOB绕着点O顺时针旋转一个角度 , (如图2),在转动过程中两块三角板都在直线EF的上方,当OB平分由OA , OC , OD其中任意两边组成的角时,求的值.
 15. 如图,O为直线上一点, , 平分 , .
15. 如图,O为直线上一点, , 平分 , . (1)、请你数一数,图中有多少个小于平角的角;(2)、求出的度数;(3)、试判断是否平分 , 并说明理由。
(1)、请你数一数,图中有多少个小于平角的角;(2)、求出的度数;(3)、试判断是否平分 , 并说明理由。四、综合题
-
16. 如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
 (1)、写出∠DOE的补角;(2)、若∠BOE=62°,求∠AOD和∠EOF的度数;(3)、试问射线OD与OF之间有什么特殊的位置关系?为什么?17. 以直线AB上一点O为端点作射线OC,使∠BOC=40°,将一个直角三角板的直角顶点放在O处,即∠DOE=90°.(1)、如图1,若直角三角板DOE的一边OE放在射线OA上,则∠COD=;
(1)、写出∠DOE的补角;(2)、若∠BOE=62°,求∠AOD和∠EOF的度数;(3)、试问射线OD与OF之间有什么特殊的位置关系?为什么?17. 以直线AB上一点O为端点作射线OC,使∠BOC=40°,将一个直角三角板的直角顶点放在O处,即∠DOE=90°.(1)、如图1,若直角三角板DOE的一边OE放在射线OA上,则∠COD=; (2)、如图2,将直角三角板DOE绕点O顺时针转动到某个位置,若OE恰好平分∠AOC,则∠COD=;
(2)、如图2,将直角三角板DOE绕点O顺时针转动到某个位置,若OE恰好平分∠AOC,则∠COD=;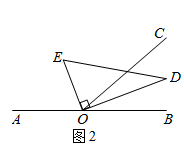 (3)、将直角三角板DOE绕点O顺时针转动(OD与OB重合时为停止)的过程中,恰好有∠COD=∠AOE,求此时∠BOD的度数.
(3)、将直角三角板DOE绕点O顺时针转动(OD与OB重合时为停止)的过程中,恰好有∠COD=∠AOE,求此时∠BOD的度数.