2023-2024学年人教版(吉林地区)初中数学七年级下册 5.1.1 相交线 同步分层训练提升题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 如图,把一块直角形的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2是( )
 A、65° B、55° C、60° D、35°2. 下列图形中,一定成立的是( )A、
A、65° B、55° C、60° D、35°2. 下列图形中,一定成立的是( )A、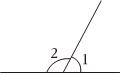 B、
B、 C、
C、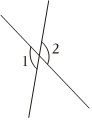 D、
D、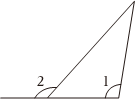 3. 平面内有7条直线,这7条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )A、16 B、22 C、20 D、184. 同一平面内互不重合的3条直线的交点的个数是( )A、可能是0,1,2 B、可能是0,2,3 C、可能是0,1,2或3 D、可能是1,可能是35. 如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型.转动木条,当∠1增大10°时,有以下两种说法:①∠2增大10°;②∠3减小10.下列说法正确的是( )
3. 平面内有7条直线,这7条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )A、16 B、22 C、20 D、184. 同一平面内互不重合的3条直线的交点的个数是( )A、可能是0,1,2 B、可能是0,2,3 C、可能是0,1,2或3 D、可能是1,可能是35. 如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型.转动木条,当∠1增大10°时,有以下两种说法:①∠2增大10°;②∠3减小10.下列说法正确的是( ) A、①对,②不对 B、①不对,②对 C、①,②均不对 D、①,②均对6. 光线从空气射入水中会发生折射现象,如图①所示.小华为了观察光线的折射现象,设计了图②所示的实验:通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块.图③是实验的示意图,点A,C,B在同一直线上,下列各角中,∠PDM的对顶角是 ( )
A、①对,②不对 B、①不对,②对 C、①,②均不对 D、①,②均对6. 光线从空气射入水中会发生折射现象,如图①所示.小华为了观察光线的折射现象,设计了图②所示的实验:通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块.图③是实验的示意图,点A,C,B在同一直线上,下列各角中,∠PDM的对顶角是 ( ) A、∠BCD B、∠FDB C、∠BDN D、∠CDB7. 如图,直线相交于点O , 平分 , 若 , 则的度数是( )
A、∠BCD B、∠FDB C、∠BDN D、∠CDB7. 如图,直线相交于点O , 平分 , 若 , 则的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 命题“对顶角相等”改写成如果 , 那么.9. 如图,已知∠1=∠7,那么∠4和∠8的关系是 , ∠2和∠7的关系是.
 10. 如图,直线AB,CD相交于点O,OE平分∠AOC.若∠BOD=60°,则∠AOE的度数是
10. 如图,直线AB,CD相交于点O,OE平分∠AOC.若∠BOD=60°,则∠AOE的度数是 11. 为了测量一座古塔外墙底部的底角∠AOB的度数,李潇同学设计了如下测量方案:分别作AO,BO的延长线OD,OC,量出∠COD的度数,从而得到∠AOB的度数.这个测量方案的依据是
11. 为了测量一座古塔外墙底部的底角∠AOB的度数,李潇同学设计了如下测量方案:分别作AO,BO的延长线OD,OC,量出∠COD的度数,从而得到∠AOB的度数.这个测量方案的依据是 12. 如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O,若∠BOE=40°,则∠AOC的度数为 .
12. 如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O,若∠BOE=40°,则∠AOC的度数为 .
三、解答题
-
13. 如图,直线l1 , l2被直线l3所截如果∠1与∠3相等,那么∠2与∠3互补,∠2与∠4相等.试说明理由(填空).

理由:∵∠1=∠3( ),
∵∠1+∠2=(平角的意义),
∴∠2+=180°,
∴∠2与∠3互补(互补的意义).
∵∠4+∠3=(平角的意义),
∴∠2=∠4( ).
14. 已知:点为直线上一点,过点作射线 , . (1)、如图1,求的度数;(2)、如图2,过点作射线 , 使 , 作的平分线 , 求的度数;(3)、如图3,在(2)的条件下,作射线 , 若与互余,请画出图形,并求的度数.
(1)、如图1,求的度数;(2)、如图2,过点作射线 , 使 , 作的平分线 , 求的度数;(3)、如图3,在(2)的条件下,作射线 , 若与互余,请画出图形,并求的度数.四、综合题