备战2024年中考数学细点逐一突破真题训练第4章一元二次方程及其应用-在线组卷题库

1. 下列方程中，关于x的一元二次方程是（）

A、 $x^{2} + 2 x = x^{2} - 1$ B、 $a x^{2} + b x + c = 0$ C、 $3 (x + 1)^{2} = 2 (x + 1)$ D、 $\frac{1}{x^{2}} + \frac{1}{x} - 2 = 0$

查看试题解析
2. 若 $a ， b (a < b)$ 是关于方程 $(x - m) (x - n) + 1 = 0 (m < n)$ 的两个实数根，则实数 $a ， b ， m ， n$ 的大小关系是（）

A、 $a < b < m < n$ B、 $m < n < a < b$ C、 $a < m < n < b$ D、 $m < a < b < n$

查看试题解析
3. 已知关于x的方程 $x^{2} - (2 k + 1) x + (3 k - 1) = 0$ .

(1)、求证：无论k取任何实数，该方程都有两个不相等的实数根；

(2)、当该方程的一个根为1时，求k的值及该方程的另一个根.

查看试题解析

4. 一元二次方程x²﹣3x+3＝0的根的情况是（）．

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、不能确定

查看试题解析
5. 直线 $y = x + a$ 不经过第二象限，则关于 $x$ 的方程 $a x^{2} + 2 x + 1 = 0$ 实数解的个数是（）.

A、0个 B、1个 C、2个 D、1个或2个

查看试题解析
6. 已知关于x的一元二次方程kx²﹣（2k﹣1）x+k﹣2＝0有两个不相等的实数根，则实数k的取值范围是（）

A、k＞﹣ $\frac{1}{4}$ B、k＜ $\frac{1}{4}$ C、k＞﹣ $\frac{1}{4}$ 且k≠0 D、k＜ $\frac{1}{4}$ 且k≠0

查看试题解析
7. 关于 $x$ 的一元二次方程 $x^{2} + m x - 1 = 0$ ，当 $m = 1$ 时，该方程的正根称为黄金分割数 $.$ 宽与长的比是黄金分割数的矩形叫做黄金矩形，希腊的帕特农神庙采用的就是黄金矩形的设计；我国著名数学家华罗庚的优选法中也应用到了黄金分割数．

(1)、求黄金分割数；

(2)、已知实数 $a$ ， $b$ 满足： $a^{2} + m a = 1$ ， $b^{2} - 2 m b = 4$ ，且 $b \neq - 2 a$ ，求 $a b$ 的值；

(3)、已知两个不相等的实数 $p$ ， $q$ 满足： $p^{2} + n p - 1 = q$ ， $q^{2} + n q - 1 = p$ ，求 $p q - n$ 的值．

查看试题解析

8. 已知关于 $x$ 的方程 $a^{2} x^{2} + (a + 1) x + 1 = 0$ （ $a$ 为常数，且 $a \neq 0$ ），下列 $x$ 的值，哪个一定不是方程的解（）

A、 $x = - 1$ B、 $x = - 2$ C、 $x = - 3$ D、 $x = 1$

查看试题解析
9. 若关于 $x$ 的一元二次方程 $a x^{2} + 6 x - 4 = 0$ 的解为 $x_{1} = 1 ， x_{2} = 2$ ，则关于 $y$ 的一元二次方程 $a (y + 1)^{2}$ $+ 6 (y + 1) - 4 = 0$ 的解为（）

A、 $y_{1} = 1 ， y_{2} = 2$ B、 $y_{1} = 0 ， y_{2} = 2$ C、 $y_{1} = 0 ， y_{2} = 1$ D、 $y_{1} = - 1 ， y_{2} = - 2$

查看试题解析
10. 已知关于x的一元二次方程 $x^{2} - 2 x + m = 0$ 有两个不相等的实数根，设此方程的一个实数根为b，令 $y = 4 b^{2} - 8 b + 3 m + 2$ ，则（）

A、 $y > 1$ B、 $y \geq 1$ C、 $y \leq 1$ D、 $y < 1$

查看试题解析
11. 三国时期的数学家赵爽在其所著的《勾股圆方图注》中记载了用几何法对一元二次方程进行求解的方法，以 $x^{2} - 2 x - 3 = 0$ 为例，大致过程如下：

第一步：将原方程变形为 $x^{2} - 2 x = 3$ ．即 $x (x - 2) = 3$ ．

第二步：构造一个长为 $x$ ，宽为 $(x - 2)$ 的长方形，长比宽大2，且面积为3，如图①所示．

第三步：用四个这样的长方形围成一个大正方形，中间是一个小正方形，如图②所示．

第四步：

将大正方形边长用含 $x$ 的代数式表示为____．

小正方形边长为常数____，

长方形面积之和为常数____．

由观察可得，大正方形面积等于四个长方形与小正方形面积之和，得方程____，两边开方可求得 $x_{1} = 3$ ， $x_{2} = - 1$ ．

(1)、第四步中横线上应依次填入，，，；

(2)、请参考古人的思考过程，画出示意图，写出步骤，解方程 $x^{2} - x - 3 = 0$ ．

查看试题解析
12. 当解某些计算较复杂的一元二次方程时，可考虑用“缩根法”简化运算．“缩根法”是指将一元二次方程先转化成系数比原方程简单的新一元二次方程，然后解新一元二次方程，并将新方程的两根同时缩小，从而得到原方程的两个根．
已知：关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个根分别为 $x_{1} = α$ ， $x_{2} = β$ ，求关于 $x$ 的一元二次方程 $p^{2} a x^{2} + p b x + c = 0 (a p \neq 0)$ 的两根．
解：因为 $p^{2} a x^{2} + p b x + c = 0 (a p \neq 0)$ ，
所以 $a {(p x)}^{2} + b \cdot p x + c = 0$ ．
令 $p x = x^{'}$ ，得新方程 $a {x^{'}}^{2} + b x^{'} + c = 0$ ．
因为新方程的解为 ${x^{'}}_{1} = α$ ， ${x^{'}}_{2} = β$ ，所以 $p x = α$ ， $p x = β$ ，所以原方程的两个根分别为 $x_{1} = \frac{α}{p}$ ， $x_{2} = \frac{β}{p}$ ．
这种解一元二次方程的方法叫做“缩根法”．
举例：用缩根法解方程 $49 x^{2} + 35 x - 24 = 0$ ．
解：因为 $49 = 7^{2}$ ， $35 = 5 \times 7$ ，所以 ${(7 x)}^{2} + 5 \times 7 x - 24 = 0$ ，令 $7 x = x^{'}$ ，得新方程 ${x^{'}}^{2} + 5 x^{'} - 24 = 0$ ．
解新方程，得 ${x^{'}}_{1} = 3$ ， ${x^{'}}_{2} = - 8$ ，所以 $7 x = 3$ ， $7 x = - 8$ ，
所以原方程的两个根分别为 $x_{1} = \frac{3}{7}$ ， $x_{2} = - \frac{8}{7}$ ．
请利用上面材料中的缩根法解下列方程：

(1)、 $36 x^{2} - 6 x - 1 = 0$ ；

(2)、 $3 x^{2} + 160 x - 256000 = 0$ ．

查看试题解析
13. 请阅读下列材料：
问题：已知方程 $x^{2} + x - 1 = 0$ ，求一个一元二次方程，使它的根分别是已知方程根的2倍．
解：设所求方程的根为 $y$ ，则 $y = 2 x$ ，所以 $x = \frac{y}{2}$ ，把 $x = \frac{y}{2}$ 代入已知方程，得 ${(\frac{y}{2})}^{2} + \frac{y}{2} - 1 = 0$ ；化简，得 $y^{2} + 2 y - 4 = 0$ ；故所求方程为 $y^{2} + 2 y - 4 = 0$ ．
这种利用方程根的代换求新方程的方法，我们称为“换根法”；
请用阅读材料提供的“换根法”求新方程（要求：把所求方程化为一般形式）：

(1)、已知方程 $x^{2} + 3 x - 2 = 0$ ，求一个一元二次方程，使它的根分别为已知方程根的相反数；

(2)、已知关于 $x$ 的一元二次方程 $a x^{2} - b x + c = 0 (a \neq 0)$ 有两个不等于零的实数根，求一个一元二次方程，使它的根分别是已知方程根的倒数．

查看试题解析
14. 根据以下材料，完成题目．
材料一：数学家欧拉为了解决一元二次方程 $x^{2} = - 1$ 在实数范围内无解的问题，引进虚数单位 $i$ ，规定 $i^{2} = - 1$ ．当 $b \neq 0$ 时，形如 $a + b i$ （ $a$ ， $b$ 为实数）的数统称为虚数．比如 $5 i$ ， $3 + 2 i$ ， $1 - \sqrt{2} i$ ．当 $b = 0$ 时， $a + b i = a + 0 \cdot i = a$ 为实数．

材料二：虚数的运算与整式的运算类似，任意两个虚数 $a + b i$ ， $c + d i$ （其中 $a$ ， $b$ ， $c$ ， $d$ 为实数．且 $b \neq 0$ ， $d \neq 0$ ）有如下运算法则

$(a + b i) + (c + d i) = (a + c) + (b + d) i$

$(a + b i) - (c + d i) = (a - c) + (b - d) i$

$(a + b i) \cdot (c + d i) = a c + a d i + b c i + b d i^{2} = (a c - b d) + (a d + b c) i$

材料三：关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0$ （ $a$ ， $b$ ， $c$ 为实数且a≠0）如果没有实数根，那么它有两个虚数根，求根公式为 $x = \frac{- b \pm \sqrt{4 a c - b^{2}} \cdot i}{2 a}$ ．

解答以下问题：

(1)、填空：化简 $i^{4} =$ ， $(1 + i)^{2} =$ ；

(2)、关于 $x$ 的一元二次方程 $x^{2} + m x + n = 0$ 有一个根是 $1 + i$ ，其中 $m$ ， $n$ 是实数，求 $m + n$ 的值；

(3)、已知关于 $x$ 的一元二次方程 $x^{2} - 3 x - k + 4 = 0$ 无实数根，且 $k$ 为正整数，求该方程的虚数根．

查看试题解析

15. 电影《满江红》在2023年春节档上映，深受观众喜爱．某电影院每日开放若干个能容纳80位观众的放映厅排片《满江红》，票价统一订为60元．经调查发现，当一天排片3个放映厅时，每个厅均能坐满．在此基础上，每增加1个厅，每个厅将减少10位观众．若该电影院拟一日票房收入为18000元，设需要增加开放x个放映厅，根据题意可列出方程为（）

A、 $60 (3 - x) (80 + 10 x) = 18000$ B、 $60 (3 + x) (80 - 10 x) = 18000$ C、 $60 (3 + x) (110 - 10 x) = 18000$ D、 $60 (3 - x) (50 + 10 x) = 18000$

查看试题解析
16. 某纪念品原价168元，连续两次降价 $a %$ 后售价为128元；下列所列方程正确的是（）

A、 $160 {(1 + a %)}^{2} = 128$ B、 $160 {(1 - a %)}^{2} = 128$ C、 $160 {(1 - 2 a %)}^{2} = 128$ D、 $160 (1 - a %) = 128$

查看试题解析
17. 年糕饺是宁波的特色美食，其以年糕为皮，可咸可甜的馅料裹于其中，口感软糯平实．今有某店铺销售年糕饺，通过分析销售情况发现，年糕饺的日销售量y（盒）是销售单价x（元/盒）的一次函数，销售单价、日销售量的部分对应值如下表，已知销售单价不低于成本价．当店铺将销售单价定为18元/盒时，日销售利润为750元．
销售单价x（元/盒）
15
17
日销售量y（盒）
150
100

(1)、求年糕饺的日销售量y（盒）关于销售单价x（元/盒）的函数表达式．

(2)、求年糕饺每盒的成本价．

(3)、端午节，为了尽可能让利顾客，扩大销售，店铺采用了降价促销的方式，当销售单价x（元/盒）定为多少时，日销售利润为1000元？

查看试题解析

18. 一件商品的原价是300元，连续两次降价后，现售价是243元，若每次降价的百分率相同，那么这个百分率为．

查看试题解析
19. $2023$ 年 $4$ 月 $23$ 是第 $28$ 个世界读书日，读书已经成为很多人的一种生活方式，城市书院是读书的重要场所之一，据统计，某书院对外开放的第一个月进书院 $600$ 人次，进书院人次逐月增加，到第三个月末累计进书院 $2850$ 人次，若进书院人次的月平均增长率为 $x$ ，则可列方程为（）

A、 $600 (1 + 2 x) = 2850$ B、 $600 {(1 + x)}^{2} = 2850$ C、 $600 + 600 (1 + x) + 600 {(1 + x)}^{2} = 2850$ D、 $2850 {(1 - x)}^{2} = 600$

查看试题解析
20. 新能源汽车已逐渐成为人们的交通工具.某品牌新能源汽车经销商对新上市的A汽车在1月份至3月份的销售情况进行统计，发现A汽车1月份的销量为20辆，3月份的销量为45辆.

(1)、求A汽车销量的月平均增长率.

(2)、为了扩大A汽车的市场占有量，提升A汽车的销售业绩，该公司决定采取适当的降价措施（降价幅度不超过售价的10%）.经调查发现，当A汽车的销售单价定为12万元时，平均每月的售量为30辆，在此基础上，若A汽车的销售单价每降1万元，平均每月可多售出10辆，若销售额要达到440万元，则每辆A汽车需降价多少万元？

查看试题解析

21. 如图，在一块长为 $20 m$ ，宽为 $12 m$ 的矩形 $A B C D$ 空地内修建四条宽度相等，且与矩形各边垂直的道路，四条道路围成的中间部分恰好是一个正方形，且边长是道路宽的4倍，道路占地总面积为 $40 m^{2}$ ，设道路宽为 $x m$ ，则以下方程正确的是（）

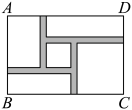A、 $32 x + 4 x^{2} = 4$ B、 $32 x + 8 x^{2} = 40$ C、 $64 x - 4 x^{2} = 40$ D、 $64 - 8 x^{2} = 40$

查看试题解析
22. 某农场要建一个饲养场（矩形 $A B C D$ ），两面靠墙（ $A D$ 位置的墙最大可用长度为25m， $A B$ 位置的墙最大可用长度为21m），另外两边用木栏围成，中间用木栏隔成两个小矩形并在如图所示的两处各留1m宽的门（不用木栏），建成后木栏总长50m．

(1)、若饲养场（矩形 $A B C D$ ）的面积为 $240 m^{2}$ ，求边 $C D$ 的长；

(2)、小芳说：“饲养场的面积最多能达到 $338 m^{2}$ ． ”若能达到，求出边 $C D$ 的长；若不能达到，请说明理由．

查看试题解析
23. 如图，用总长为80米的篱笆，在一面靠墙的空地上围成如图所示的花圃ABCD ，花圃中间有一条2米宽的人行通道，园艺师傅用篱笆围成了四个形状、大小一样的鲜花种植区域，鲜花种植总面积为192平方米，花圃的一边靠墙，墙长20米，求AB和BC的长.

查看试题解析

24. 2022年底，新冠疫情持续蔓延，若一人携带病毒未进行有效隔离，经过两轮传染后共有441人感染，设每轮传染中平均每个人传染了 $x$ 人，则根据题意可列出方程（）

A、 $x (1 + x) = 441$ B、 $x + {(1 + x)}^{2} = 441$ C、 $x + x (1 + x) = 441$ D、 $1 + x + x (1 + x) = 441$

查看试题解析
25. 某市要组织一次篮球联赛，比赛制为单循环形式（每两队之间都赛一场），计划安排45场比赛，若设有 $x$ 支球队参加比赛，则所列方程正确的是（）

A、 $x (x - 1) = 45$ B、 $\frac{1}{2} x (x - 1) = 45$ C、 $x (x + 1) = 45$ D、 $\frac{1}{2} x (x + 1) = 45$

查看试题解析

26. 如图所示， $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 6 c m$ ， $B C = 8 c m$ .

(1)、点 $P$ 从点 $A$ 开始沿 $A B$ 边向 $B$ 以 $1 c m / s$ 的速度移动，点 $Q$ 从 $B$ 点开始沿 $B C$ 边向点 $C$ 以 $2 c m / s$ 的速度移动.如果 $P$ ， $Q$ 分别从 $A$ ， $B$ 同时出发，经过几秒，使 $△ P B Q$ 的面积等于 $8 c m^{2}$ ？

(2)、在（1）的运动情况下，线段 $P Q$ 能否将 $△ A B C$ 分成面积相等的两部分？若能，求出运动时间；若不能说明理由.

(3)、若 $P$ 点沿射线 $A B$ 方向从 $A$ 点出发以 $1 c m / s$ 的速度移动，点 $Q$ 沿射线 $C B$ 方向从 $C$ 点出发以 $2 c m / s$ 的速度移动， $P$ ， $Q$ 同时出发，问几秒后， $△ P B Q$ 的面积为 $1 c m^{2}$ ？

查看试题解析
27. 在欧几里得的《几何原本》中，形如 $x^{2} + a x = b^{2}$ 的一元二次方程通过图解法能得到其中的一个正根：如图，先画Rt△ACB，使∠ACB=90°，BC= $\frac{a}{2}$ ， AC=b，再在斜边AB上截取 $B D = \frac{a}{2} ，$ 连结CD，那么图中某条线段的长就是一元二次方程的其中一个正根.

(1)、用含a，b的代数式表示AD的长.

(2)、图中哪条线段的长是一元二次方程 $x^{2} + a x = b^{2}$ 的一个正根?请说明理由.

查看试题解析
28. 综合与实践
问题情景：小琴在延时服务剪纸课上发现了奇妙的数学知识，可以利用方程解决剪纸问题中的剩余面积问题．

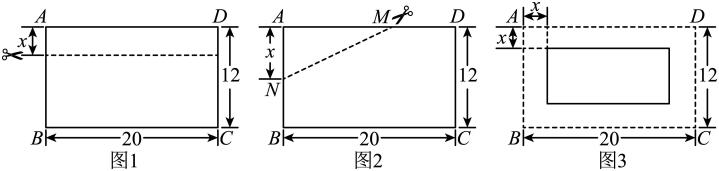(1)、独立思考：如图1，长方形纸片 $A B C D$ 长为 $20 c m$ ，宽为 $12 c m$ ，按如图方式剪下一个宽为 $x c m$ 的小长方形，若剩余长方形面积为 $200 c m^{2}$ ，则x的值为．

(2)、实践探究：如图2，M为 $A D$ 上一点，N为 $A B$ 上一点，且 $A M = 2 A N = 2 x (c m)$ ，沿着 $M N$ 剪下一个 $△ A M N$ ，若剩余部分图形面积为 $204 c m^{2}$ ，求x的值．

(3)、问题解决：如图3，将长方形纸片 $A B C D$ 剪掉一个宽为 $x c m$ 的边框，剩余面积能否为 $180 c m^{2}$ ，若能，请求出x的值；若不能，请说明理由．

查看试题解析

29. 若x为实数，且满足 $x^{2} + \frac{1}{x^{2}} - 2 (x + \frac{1}{x}) - 1 = 0$ ，则 $x + \frac{1}{x} =$ （　　）

A、 $- 1$ B、 $3$ C、 $- 1$ 或 $3$ D、无法确定

查看试题解析
30. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
①若 $a + b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；③若 $c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = (2 a x_{0} + b)^{2}$ ；⑤存在实数 $m ， n (m \neq n)$ ，使得 $a m^{2} + b m + c = a n^{2} + b n + c$ ．
其中正确的（）

A、只有①②④ B、只有①②④⑤ C、①②③④⑤ D、只有①②③

查看试题解析
31. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
①若 $a + b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；
②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；
③若c是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；
④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$ 其中正确的（）

A、只有①②④ B、只有①②③ C、①②③④ D、只有①②

查看试题解析
32. 已知 $a (a > 1)$ 是关于x的方程 $x^{2} - b x + b - a = 0$ 的实数根．下列说法：①此方程有两个不相等的实数根；②当 $a = t ＋ 1$ 时，一定有 $b = t - 1$ ；③b是此方程的根；④此方程有两个相等的实数根．上述说法中，正确的有（）

A、①② B、②③ C、①③ D、③④

查看试题解析
33. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
$①$ 若 $a + b + c = 0$ ，则方程必有一根为 $x = 1$ ；
$②$ 若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 无实根；
$③$ 若方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 两根为 $x_{1}$ ， $x_{2}$ 且满足 $x_{1} \neq x_{2} \neq 0$ ，则方程 $c x^{2} + b x + a = 0 (c \neq 0)$ ，必有实根 $\frac{1}{x_{1}}$ ， $\frac{1}{x_{2}}$ ；
$④$ 若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = (2 a x_{0} + b)^{2}$ ．
其中正确的（）

A、 $① ②$ B、 $① ④$ C、 $② ③ ④$ D、 $① ③ ④$

查看试题解析

备战2024年中考数学细点逐一突破真题训练第4章一元二次方程及其应用

一、一元二次方程定义

二、一元二次方程根与系数的关系

三、一元二次方程解法

四、销售利润问题

五、增长率问题

六、面积问题

七、传染病，比赛问题

八、几何综合-方程思想

九、一元二次方程多结论问题

销售单价x（元/盒）	15	17
日销售量y（盒）	150	100