江西省抚州市临川区2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2024-01-26 类型：期中考试

进入 出卷网 下载

一、选择题（本大题共6个小题，每小题3分，共18分，每小题只有一个正确选项）

  • 1. 某班从甲、乙、丙、丁四位选手中随机选取两人参加校乒乓球比赛，恰好选中甲、乙两位选手的概率是（　　）
    A、18 B、16 C、14 D、13

    查看试题解析

  • 2. 根据下列表格对应值：

    x

    2.1

    2.2

    2.3

    2.4

    2.5

    ax2+bx+c

    ﹣0.12

    ﹣0.03

    ﹣0.01

    0.06

    0.18

    判断关于x的方程ax2+bx+c＝0（a≠0）的一个解x的范围是（    ）

    A、2.1＜x＜2.2 B、2.2＜x＜2.3 C、2.3＜x＜2.4 D、2.4＜x＜2.5

    查看试题解析

  • 3. 下列命题是真命题的是（  ）
    A、对角线相等的四边形是平行四边形 B、对角线互相平分且相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分的四边形是正方形

    查看试题解析

  • 4. 若关于x的一元二次方程ax2﹣2x+1=0有两个实数根，则实数a的取值范围是（   ）
    A、a≤1且a≠0 B、a＜1且a≠0 C、a≤1 D、a＜1

    查看试题解析

  • 5. 菱形ABCD的一条对角线的长为6，边AB的长是方程x2﹣7x+12＝0的一个根，则菱形ABCD的周长为（　　）
    A、16 B、12 C、12或16 D、无法确定

    查看试题解析

  • 6. 如图，矩形ABCD中，对角线AC，BD相交于点O，AD＝23 ， ∠COB＝60°，BF⊥AC，交AC于点M，交CD于点F，延长FO交AB于点E，则下列结论：①FO＝FC；②四边形EBFD是菱形；③△OBE≌△CBF；④MB＝3．其中结论正确的序号是（　　）

    A、②③④ B、①②③ C、①④ D、①②③④

    查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

  • 7. 假定鸟卵孵化后，雏鸟为雌鸟与为雄鸟的概率相同．如果三枚卵全部成功孵化，则三只雏鸟中恰有两只雄鸟的概率为 ．

    查看试题解析

  • 8. 某超市一月份的营业额为30万元，三月份的营业额为56万元．设每月的平均增长率为x，则可列方程为 ．

    查看试题解析

  • 9. 关于x的代数式x2+（m+2）x+（4m﹣7）中，当m=时，代数式为完全平方式．

    查看试题解析

  • 10. 已知：在四边形ABCD中，AD＝BC，点E，F，G，H分别是AB，CD，AC，BD的中点，四边形EHFG是  ．

    查看试题解析

  • 11. 已知菱形的两条对角线分别是一元二次方程x2﹣14x+48＝0的两个实数根，则该菱形的面积是 ．

    查看试题解析

  • 12. 在▱ABCD中，AB＝4，∠ABC，∠BCD的平分线BE，CF分别与直线AD交于点E，F，当点A，D，E，F相邻两点间的距离相等时，BC的长为  ．

    查看试题解析

三、（本大题共5小题，每小题6分，共30分）

  • 13. 解一元二次方程．
    (1)、x2﹣4x﹣7＝0；
    (2)、（2x+1）2﹣4（2x+1）＝0．

    查看试题解析

  • 14. 如图，在▱ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F，连接EF．求证：四边形ABEF是菱形．

    查看试题解析

  • 15. 将分别标有数字1，2，3的三张卡片洗匀后，背面朝上放在桌面上．
    (1)、随机地抽取一张，求抽到偶数的概率；
    (2)、请你通过列表或画树状图分析：随机地抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，能组成哪些两位数？恰好是“4的倍数”的概率为多少？

    查看试题解析

  • 16. 已知四边形ABCD是平行四边形，BD为对角线，分别在图①、图②中按要求作图（保留作图痕迹，不写作法）．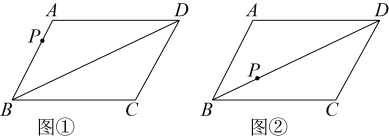

    (1)、如图①，点P为AB上任意一点，请仅用无刻度的直尺在CD上找出另一点Q，使AP＝CQ；
    (2)、如图②，点P为BD上任意一点，请仅用无刻度的直尺在BD上找出一点Q，使BP＝DQ．

    查看试题解析

  • 17. 如图，在一块长92m、宽60m的矩形耕地上挖三条水渠（水渠的宽都相等），水渠把耕地分成面积均为885m2的6个矩形小块，水渠应挖多宽？

    查看试题解析

四、（本大题共3小题，每小题8分，共24分）

  • 18. 已知a是方程x2﹣2020x+1＝0的一个根．求：
    (1)、2a2﹣4040a﹣3的值；
    (2)、代数式a2﹣2019a+ 2020a2+1的值．

    查看试题解析

  • 19. 某商场销售某种冰箱，每台进货价为2500元，标价为3000，
    (1)、若商场连续两次降价，每次降价的百分率相同，最后以2430元售出，求每次降价的百分率；
    (2)、市场调研表明：当每台售价为2900元时，平均每天能售出8台，当每台售价每降50元时，平均每天就能多售出4台，若商场要想使这种冰箱的销售利润平均每天达到5000元，则每台冰箱的定价应为多少元？

    查看试题解析

  • 20. 如图，在矩形ABCD中，点E，F分别在边AB，BC上，AF⊥DE，且AF＝DE，AF与DE相交于点G．

    (1)、求证：矩形ABCD为正方形：
    (2)、若AE：EB＝2：1，△AEG的面积为4，求四边形BEGF的面积．

    查看试题解析

五、（本大题共2小题，每小题9分，共18分）

  • 21. 根据“五项管理”文件精神，某学校优化学校作业管理，探索减负增效新举措，学校就学生做作业时间进行问卷调查，将收集信息进行统计分成A、B、C、D四个层级，其中A：90分钟以上；B：60～90分钟；C：30～60分钟；D：30分钟以下．并将结果绘制成两幅不完整的统计图，请你根据统计信息解答下列问题：

    (1)、接受问卷调查的学生共有 人；
    (2)、求扇形统计图中“D”等级的扇形的圆心角的度数，并补全条形统计图；
    (3)、全校约有学生1500人，估计“A”层级的学生约有多少人？
    (4)、学校从“A”层级的3名女生和2名男生中随机抽取2人参加现场深入调研，则恰好抽到1名男生和1名女生的概率是多少？

    查看试题解析

  • 22. 如图，在四边形ABCD中，AD∥BC，∠B＝90°，AB＝8cm，AD＝20cm，BC＝24cm，P、Q分别从A、C同时出发，向D，B运动．当一个点到达端点时，停止运动，另一个点也停止运动．

    (1)、如果P、Q的速度分别为1cm/s和3cm/s．运动时间为t秒，则t为何值时，PQ＝DC．并说明理由．
    (2)、如果P的速度为1cm/s，其他条件不变，要使四边形APQB是矩形，且矩形的长宽之比为2：1，求Q点运动的速度．

    查看试题解析

六、（本大题共12分）

  • 23. 已知，如图1，BD是边长为1的正方形ABCD的对角线，BE平分∠DBC交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G.

    (1)、求证：△BCE≌△DCF；
    (2)、求CF的长；
    (3)、如图2，在AB上取一点H，且BH=CF，若以BC为x轴，AB为y轴建立直角坐标系，问在直线BD上是否存在点P，使得以B、H、P为顶点的三角形为等腰三角形？若存在，直接写出所有符合条件的P点坐标；若不存在，说明理由.

    查看试题解析