吉林省吉林九中2022-2023学年八年级上学期期中数学试卷

试卷更新日期：2024-01-26 类型：期中考试

进入出卷网下载

一、选择题（每小题2分，共12分）

1. 下列分式中属于最简分式的是（　　）

A、 $\frac{4}{2 x}$ B、 $\frac{x^{2}}{x y}$ C、 $\frac{2 x}{x^{2} + 1}$ D、 $\frac{x - 1}{x^{2} - 1}$

查看试题解析
2. 下列四个图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 计算（﹣a²）³÷a⁴结果是（　　）

A、﹣a² B、a² C、﹣a³ D、a³

查看试题解析
4. 如果把分式 $\frac{10 x y}{x + y}$ 中的x，y都扩大10倍，则分式的值（　　）

A、缩小10倍 B、扩大10倍 C、不变 D、缩小到原来的 $\frac{1}{10}$

查看试题解析
5. 如图，△ABC是等边三角形，点D在AC边上，∠DBC＝40°，则∠ADB的度数为（）

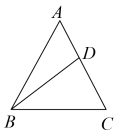A、25° B、60° C、90° D、100°

查看试题解析
6. 某文具店购进A，B两种款式的书包，其中A种书包的单价比B种书包的单价低10%．已知店主购进A种书包用了810元，购进B种书包用了600元，且所购进的A种书包的数量比B种书包多20个．设文具店购进B种款式的书包x个，则所列方程正确的是（　　）

A、 $\frac{810}{x + 20} = \frac{600}{x} \times 10 %$ B、 $\frac{600}{x} = \frac{810}{x + 20} \times 10 %$ C、 $\frac{810}{x + 20} = \frac{600}{x} (1 - 10 %)$ D、 $\frac{810}{x (1 - 10 %)} = \frac{600}{x} \times (x + 20)$

查看试题解析

二、填空题（每小题3分，共24分）

7. 分式 $\frac{2 x + 1}{x - 1}$ 有意义，则x的取值范围是．

查看试题解析
8. 分解因式：a³﹣6a²＝．

查看试题解析
9. 计算： $\frac{1}{2}$ xy²•（﹣4x²y）＝．

查看试题解析
10. “KN95”口罩能过滤空气中95%的直径约为 $0.0000003 m$ 的非油性颗粒，数据0.0000003用科学记数法表示为.

查看试题解析
11. 如图，在△ABC中，AB＝AC，AB的垂直平分线交AC于点E，已知△BCE的周长是15，AC比BC长3，则AC长为．

查看试题解析
12. 若关于x的分式方程 $\frac{1}{x - 2} + 3 = \frac{a - x}{x - 2}$ 无解，则a的值是．

查看试题解析
13. 如图，在△DBC中，∠D＝90°，点A在BD上．若AB＝AC＝10，∠ABC＝15°，则CD的长为．

查看试题解析
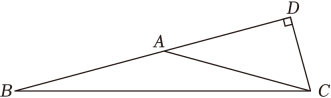14. 如图是一个残缺不全的三角形纸片，小明通过测量发现AB＝10cm，∠CAB＝∠DBA＝60°，则三角形纸片破损前的周长为 cm．

查看试题解析

三、解答题（每小题5分，共20分）

15. 解方程： $\frac{1}{x} = \frac{6}{x + 3}$ ．

查看试题解析
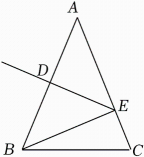
16. 计算： ${(\frac{b}{2 a})}^{2} \div {(- \frac{a}{b^{2}})}^{- 3}$ ．

查看试题解析
17. 化简：（x+y）（x﹣3y）+（2x²y+6xy²）÷2x．

查看试题解析
18. 如图，△ECB中，∠CEB＝∠B，延长BE至点A，过点A作AD∥CE，∠A＝60°，连接CD．
求证：△ECB是等边三角形．

查看试题解析

四、解答题（每小题7分，共28分）

19. 先化简，再求值： $(1 + \frac{2}{x - 1}) \div \frac{x^{2} - 1}{2 x - 2}$ ，其中x＝﹣5．

查看试题解析
20. 某市为积极响应“绿水青山就是金山银山”的号召，加强了河道整治．某工程队原计划在规定时间内整治河道1500m，实际施工时工作效率提高了20%，结果提前2天完成，求原计划规定多少天完成？

查看试题解析
21. 如图，某区有一块长为 $a + 4 b$ ，宽为 $a + 3 b$ 的长方形地块，规划部门计划将阴影部分进行绿化，中间的边长为 $a + b$ 的空白的正方形地块将修建一个凉亭．

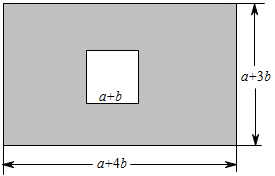(1)、用含有 $a$ 、 $b$ 的式子表示绿化总面积；

(2)、若 $a = 2$ ， $b = 5$ ，求出此时的绿化总面积．

查看试题解析
22. 如图，△ABC的三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．

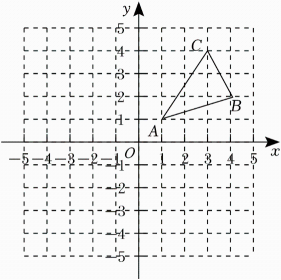(1)、直接写出点C关于x轴对称的点C₁的坐标；

(2)、画出△ABC关于y轴对称的△A₂B₂C₂ ，并写出点B的对应点B₂的坐标；

(3)、在x轴上求作一点P，使点P到A、B两点的距离和最小，请标出点P．

查看试题解析

五、解答题（每小题8分，共16分）

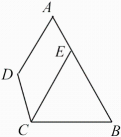
23. 如图，在△ABC中，AC＝BC，点F为AB的中点，边AC的垂直平分线交AC，CF，CB于点D，O，E，连接OB．

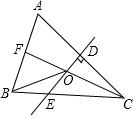(1)、求证：△OBC为等腰三角形；

(2)、若∠ACF＝23°，求∠BOE的度数．

查看试题解析
24. 探究题
图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

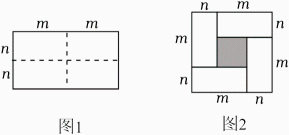(1)、请你用两种不同的代数式表示图2中阴影部分面积：
①；② ．

(2)、观察图2，写出三个代数式（m+n）² ，（m﹣n）² ， 4mn之间的等量关系：．

(3)、根据（2）中的等量关系，解决如下问题：
若|a+b﹣8|+（ab﹣7）²＝0，求（a﹣b）²的值．

查看试题解析

六、解答题（每小题10分，共20分）

25. 某中学在健维商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍，且购买一个乙种足球比购买一个甲种足球多花20元．

(1)、求购买一个甲种足球、一个乙种足球各需多少元？

(2)、为响应“足球进校园”的号召，该中学决定再次购买甲、乙两种足球共50个．恰逢健维商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了10%，乙种足球售价比第一次购买时降低了20%，如果此次购买甲、乙两种足球的总费用不超过2780元，那么该中学最多可购买多少个乙种足球？

查看试题解析
26. 如图，在△ABC中，∠ACB＝90°，AB＝5，AC＝4，BC＝3．点P从点C出发，以每秒2个单位长度的速度沿CA﹣AB向终点B运动，设点P运动的时间为t秒（t＞0）．

(1)、当点P在AB上运动时，AP的长为（用含t的式子表示）；

(2)、当△PCB是等腰直角三角形时，求t的值；

(3)、当△PAC是以AC为腰的等腰三角形时，求t的值；

(4)、当CP将△ABC分成的两部分的面积比为1：2时，求t的值．

查看试题解析