吉林省吉林九中2022-2023学年九年级上学期第一次月考数学试卷
试卷更新日期：2024-01-26 类型：月考试卷
一、选择题（每小题2分，共12分）
-
1. 二次函数y＝﹣x2+9的图象的顶点坐标是（ ）A、（0，﹣9） B、（0，9） C、（9，0） D、（﹣9，0）2. 下面四幅图是我国一些博物馆的标志，其中既是轴对称图形又是中心对称图形的是（ ）A、温州博物馆
B、西藏博物馆
C、广东博物馆
D、湖北博物馆
3. 如果关于x的一元二次方程ax2+bx+1＝0的一个解是x＝1，则代数式a+b的值为（ ）A、﹣1 B、1 C、﹣2 D、24. 抛物线y＝﹣x2+bx+c的部分图象如图所示，若y＜0，则x的取值范围是（ ）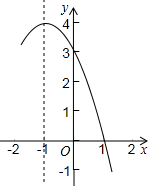
A、x＜﹣4或x＞1 B、x＜﹣3或x＞1 C、﹣4＜x＜1 D、﹣3＜x＜15. 将点A（4，1）绕原点O按顺时针方向旋转90°到点B，则点B的坐标是（ ）A、（1，﹣4） B、（4，﹣1） C、（﹣4，1） D、（﹣1，4）6. 如图，一个移动喷灌架喷射出的水流可以近似地看成抛物线，喷水头的高度（即OB的长度）是1米．当喷射出的水流距离喷水头8米时，达到最大高度1.8米，水流喷射的最远水平距离OC是（ ）
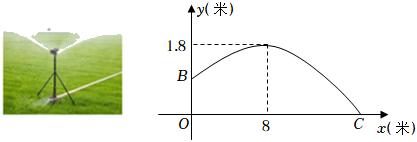A、20米 B、18米 C、10米 D、8米二、填空题（每小题3分，共24分）
-
7. 点P（5，﹣8）关于原点对称点P'的坐标为 ．8. 抛物线y＝（x﹣1）2的对称轴是直线 ．9. 如图，该图形绕着点O旋转能与自身完全重合，则旋转角最小为 °．
10. 在二次函数y＝3（x﹣6）2+1中，当x＞6时，y随x的增大而 （填“增大”或“减小”）．11. 解方程：（x﹣7）（x﹣2）＝0，则方程的两个根是x1＝ ， x2＝ ，12. 如图，将△ABC绕点C按逆时针方向旋转75°后得到△A1B1C，若∠ACB＝25°，则∠BCA1的度数为 ．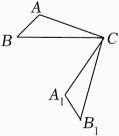
13. 请写出一个开口向下，并且与y轴交于点（0，5）的抛物线解析式 ．14. 某商店去年投资了2万元采购文具商品，由于文具商品销量较好，采购量逐年上升，预计明年用于采购文具商品的投资额达4.5万元，假设每年用于采购文具商品的投资额的平均增长率为x，则依题意可列方程为 ．三、解答题（每小题5分，共20分）
-
15. 解方程：x2+x＝6．16. 已知二次函数的图象的顶点坐标为（﹣2，﹣3），且图象过点（﹣3，﹣2），求这个二次函数的解析式．17. 如图，△ABC中，∠ABC＝60°，将△ABC绕点B逆时针旋转60°到△DBE，DE的延长线与AC相交于点F，连接DA、BF．
(1)、求证：DA∥BC；(2)、若BF＝AF＝2 ， 求DF的长．18. 图①、图②均是6×6的正方形网格，每个小正方形的顶点称为格点，小正方形的边长均为1，点A、B、C、D均在格点上，在图①，图②中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法．
(1)、在图①中以线段AB为边画一个四边形ABEF，使四边形ABEF既是轴对称图形又是中心对称图形；(2)、在图②中以线段CD为边画一个四边形CDGH，使四边形CDGH只是中心对称图形．四、解答题（每小题7分，共28分）
-
19. 已知抛物线L：y＝（m﹣2）x2+x﹣2m（m是常数且m≠2）．(1)、若抛物线L有最高点，求m的取值范围；(2)、若抛物线L与抛物线y＝x2的形状相同、开口方向相反，求m的值．20. 已知关于 x 的一元二次方程 x2﹣2(k﹣1)x+k(k+2)＝0 有两个不相等的实数根．(1)、求 k 的取值范围；(2)、写出一个满足条件的 k 的值，并求此时方程的根．21. 如图，在平面直角坐标系中，△ABC三个顶点的坐标分别是A（2，4），B（1，2），C（5，3）．
(1)、以点O为对称中心，在平面直角坐标系中画出与△ABC成中心对称的图形△A1B1C1；(2)、以点B为旋转中心，将△ABC顺时针旋转90°，得到△A2BC2 ， 在平面直角坐标系中画出△A2BC2 ．22. 平面直角坐标系中，点A坐标为（﹣1，0），直线y1＝﹣x+3与x轴交于点B，与y轴交于点C，抛物线y2＝ax2+bx+c（a≠0），经过A、B、C三点，直线x＝1.5交抛物线于点D，交BC于E，连接CD、BD．
(1)、求二次函数解析式；(2)、求△BCD的面积．五、解答题（每小题8分，共16分）
-
23. 如图，已知正方形OCDE中，顶点E（1，0），抛物线y＝x2+bx+c经过点C、D，与x轴交于A、B两点（点B在点A的右侧），直线x＝t（t≠0）交x轴于点F．
(1)、求抛物线的解析式，并直接写出点A、B的坐标；(2)、若点G是抛物线的对称轴上一动点，且使AG+CG最小，则点G的坐标为 ；(3)、在直线x＝t（第一象限部分）上找一点P，使得△OBC≌△FBP（点P与点C是对应顶点），请你直接写出点P的坐标．24. 综合与探究【问题情境】
数学活动课上，老师带领同学们一起探索旋转的奥秘．老师出示了一个问题：如图1，在△ABC中，AB＝AC，∠BAC＝90°，点D是边BC上一点 ， 连接AD，将△ABD绕着点A按逆时针方向旋转，使AB与AC重合，得到△ACE．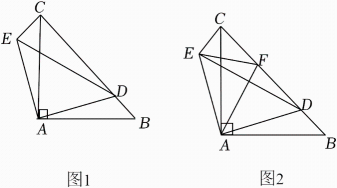
(1)、【操作探究】试判断△ADE的形状，并说明理由；(2)、【深入探究】希望小组受此启发，如图2，在线段CD上取一点F，使得∠DAF＝45°，连接EF，发现EF和DF有一定的关系，猜想两者的数量关系，并说明理由；(3)、智慧小组在图2的基础上继续探究，发现CF，FD，DB三条线段也有一定的数量关系，请你直接写出当CF＝3，BD＝2时DF的长．六、解答题（每小题10分，共20分）
-
25. 如图，在正方形ABCD中，E为AB的中点，以A为原点，AB、AD所在直线为x轴、y轴，建立平面直角坐标系．正方形ABCD的边长是方程x2﹣8x+16＝0的根．点P从点B出发，沿BC﹣CD向点D运动，同时点Q从点E出发，沿EB﹣BC向点C运动，点P的速度是每秒2个单位长度，点Q的速度是每秒1个单位长度．当点P运动到点D时，P、Q两点同时停止运动．设点P运动的时间为t秒，△APQ的面积为S．
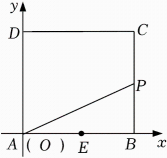(1)、求点C的坐标；(2)、求S关于t的函数关系式；(3)、当△AQP是以AP为底边的等腰三角形时，直接写出点P的坐标．26. 在平面直角坐标系中，抛物线y＝﹣x2+bx+2过点A（﹣6，﹣4）且与y轴交于点B，抛物线的顶点为C．点P为该抛物线上一动点（不与C重合），设点P的横坐标为m．
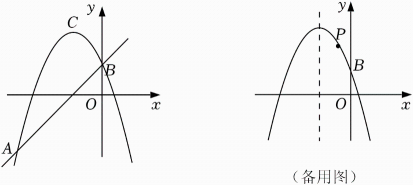(1)、抛物线的解析式为 ， 顶点C的坐标为 ；(2)、将该抛物线沿y轴向下平移2个单位长度，点P的对应点为P'，若OP＝OP'，求点P的坐标；(3)、当点P在直线AB上方的抛物线上，且点C、P到直线AB的距离相等时，求m的值；(4)、当点P在对称轴右侧时，连接BP，以BP为边作正方形BPDE，当点D恰好落在该抛物线的对称轴上时，直接写出点P的坐标．