备战2024年中考数学细点逐一突破真题训练第12章全等三角形(2)
试卷更新日期:2024-01-26 类型:一轮复习
一、基础类型(平移,翻折,轴对称)
-
1. 如图, , , .求证:.
 2. 下列判断错误的是( )A、有两角和一边对应相等的两个三角形全等 B、三条边对应相等的两个三角形全等 C、全等三角形对应边上的高相等 D、三个角对应相等的两个三角形全等3. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点到的方向平移到的位置, , , 平移距离为 , 则阴影部分面积为( )
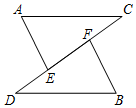
2. 下列判断错误的是( )A、有两角和一边对应相等的两个三角形全等 B、三条边对应相等的两个三角形全等 C、全等三角形对应边上的高相等 D、三个角对应相等的两个三角形全等3. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点到的方向平移到的位置, , , 平移距离为 , 则阴影部分面积为( )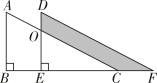 A、 B、 C、 D、4. 已知:如图,点E、F在CD上,且 , , .
A、 B、 C、 D、4. 已知:如图,点E、F在CD上,且 , , .求证:≌ .
 5. 同学们在做题时,经常用到“在直角三角形中,角所对的直角边等于斜边的一半”这个定理,下面是两种添加辅助线的证明方法,请你选择一种进行证明.
5. 同学们在做题时,经常用到“在直角三角形中,角所对的直角边等于斜边的一半”这个定理,下面是两种添加辅助线的证明方法,请你选择一种进行证明.已知:在中, ,
求证:.
方法一:如图1,在AB上取一点 , 使得 , 连接CD.
方法二:如图2,延长BC到 , 使得 , 连接AD.

我选择方法 ▲ .
证明:
二、一线三等角型
-
6. 如图,在中, , 点B在第四象限时,则点B的坐标为 .
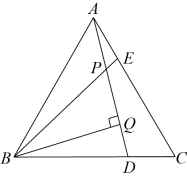
 7. 如图,在中, , . 点在线段上运动(不与 , 重合),连接 , 作 , 交线段于点 .
7. 如图,在中, , . 点在线段上运动(不与 , 重合),连接 , 作 , 交线段于点 .⑴当时,°;
⑵当时, .
 8. 如图,CD是经过顶点C的一条直线, , E , F分别是直线CD上两点,且.
8. 如图,CD是经过顶点C的一条直线, , E , F分别是直线CD上两点,且.图1
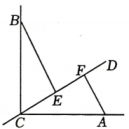 图2
图2  图3
图3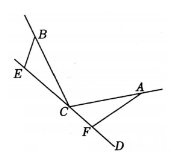 (1)、若直线CD经过的内部,且E , F在射线CD上.
(1)、若直线CD经过的内部,且E , F在射线CD上.①如图1,当时,证明:.
②如图2,若 , 当与满足什么数量关系时,①中的结论仍然成立,并说明理由.
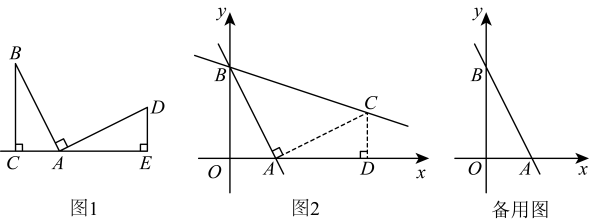
(2)、如图3,若直线CD经过的外部, , 猜想EF , BE , AF三条线段的数量关系,并证明.9. 【模型介绍】如图 , , , 过点作于点 , 过点作于点 . 则 . 我们把这个数学模型称为“字”模型或“一线三等角”模型.
【模型应用】
在平面直角坐标系中,直线与轴交于点 , 与轴交于点 .
(1)、如图 , 将直线绕点逆时针旋转 , 得到直线 , 求直线的表达式.下面是小明的想法,请你帮助完成.小明想利用“一线三等角”模型解决这个问题.如图,过点作的垂线交于点 , 再过点作轴的垂线,垂足为 , 可求出点的坐标为 , 从而求得直线的表达式为 .
(2)、若将直线绕点顺时针旋转 , 所得直线的表达式为 .(3)、点是线段上的一个动点,点是线段上一动点,若是等腰直角三角形,且 , 则点的坐标是 .10. (1)、某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC中,∠BAC=90°,AB=AC , 直线l经过点A , BD⊥直线l , CE⊥直线l , 垂足分别为点D、E.证明:DE=BD+CE.(2)、组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC , D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG , AH是BC边上的高,延长HA交EG于点I , 求证:I是EG的中点.
(1)、某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC中,∠BAC=90°,AB=AC , 直线l经过点A , BD⊥直线l , CE⊥直线l , 垂足分别为点D、E.证明:DE=BD+CE.(2)、组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC , D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG , AH是BC边上的高,延长HA交EG于点I , 求证:I是EG的中点.三、倍长中线模型
-
11. 八(2)班数学兴趣小组在一次活动中进行了探究实验活动,请你和他们一起活动吧.

[发现问题]他们在探究实验活动中遇到了下面的问题:如图1,是的中线,若 , 求的取值范围.
[探究方法]他们通过探究发现,延长至点E , 使 , 连接 . 可以证出 , 利用全等三角形的性质可将已知的边长与转化到中,进而求出的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法”.
[问题解决]
(1)、请你利用上面解答问题的思路方法,写出求的取值范围的过程.(2)、如图2,是的中线,且 , 求证: .12. 如下是某书中某一页的部分内容:如图,在中,是边的中点,过点画直线 , 使 , 交的延长线于点 , 求证:.

证明:(已知)
, (两直线平行,内错角相等).
在与中,
, (已证),
(已知),
,
(全等三角形的对应边相等).

图(1) 图(2) 图(3)
(1)、【方法应用】如图(1),在中, , 则边上的中线长度的取值范围是;(2)、【猜想证明】如图(2),在四边形中, , 点是的中点,若是的平分线,试猜想线段 , , 之间的数量关系,并证明你的猜想.(3)、【拓展延伸】如图(3),已知 , 点是的中点,点在线段上, , 若 , , 直接写出线段的长。四、十字架全等模型
-
13. 已知,正方形的四条边相等,四个角是直角.如图,点E,F分别在正方形的两边和上,与相交于点G , 且 .
 (1)、求证:;(2)、若 , 求的长度.14. 中, , , 是直线上的一个动点,连接 , 过点作的垂线,垂足为点 , 过点作的平行线交直线于点 .
(1)、求证:;(2)、若 , 求的长度.14. 中, , , 是直线上的一个动点,连接 , 过点作的垂线,垂足为点 , 过点作的平行线交直线于点 .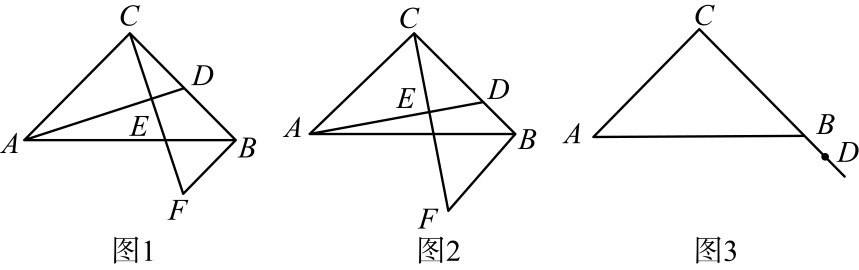 (1)、如图1,当点为中点时,请直接写出线段与的数量关系.(2)、如图2,当点在线段上不与 , 重合 , 请探究线段 , , 之间的数量关系(要求:写出发现的结论,并说明理由).(3)、如图3,当点在线段延长线上,请探究线段 , , 之间的数量关系(要求:画出图形,写出发现的结论,并说明理由).(4)、当点在线段延长线上,请直接写出线段 , , 之间的数量关系.
(1)、如图1,当点为中点时,请直接写出线段与的数量关系.(2)、如图2,当点在线段上不与 , 重合 , 请探究线段 , , 之间的数量关系(要求:写出发现的结论,并说明理由).(3)、如图3,当点在线段延长线上,请探究线段 , , 之间的数量关系(要求:画出图形,写出发现的结论,并说明理由).(4)、当点在线段延长线上,请直接写出线段 , , 之间的数量关系.五、角平分线模型
-
15. 如图,点D是△ABC三条角平分线的交点,∠ABC=68°,若AB+BD=AC , 则∠ACB的度数为 .
 16. 如图,中,、的角平分线、交于点 , 延长、 , , 则下列结论中正确的个数( )
16. 如图,中,、的角平分线、交于点 , 延长、 , , 则下列结论中正确的个数( )
平分;;; .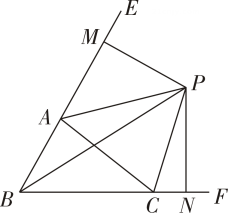 A、个 B、个 C、个 D、个17. 【教材呈现】如图是华师版八年级上册数学教材第页的部分内容.
A、个 B、个 C、个 D、个17. 【教材呈现】如图是华师版八年级上册数学教材第页的部分内容.角平分线的性质定理,角平分线上的点到角两边的距离相等.
已知:如图 , 是的平分线,点是上的任何一点, , , 垂足分别为点和点 .

求证: .
请写出完整的证明过程:
(1)、请根据教材内容,结合图 , 写出“角平分线的性质定理”完整的证明过程.(2)、【应用】如图 , 在中, , 平分 , 于点 , 点在上, , 若 , , 则的长为 .(3)、【拓展】如图 , 在中,平分交于点 , 于点 , 若 , , , , 则的面积 .18. 综合与实践(1)、问题初探如图1,在等腰直角△ABC中,∠B=90°,AB=BC,将△ABD沿着AD折叠得到△AED,AB的对应边AE落在AC上,点B的对应点为E,折痕AD交BC于点D.

求证:AC=AB+BD;
(2)、方法迁移如图2,AD是△ABC的角平分线,∠C=2∠B.求证:AB=AC+DC;
 (3)、问题拓展
(3)、问题拓展如图3,在△ABC中,∠ABC=2∠C,AD是△ABC的外角的平分线,交CB的延长线于点D.请你直接写出线段AC,AB,BD之间的数量关系.

六、手拉手模型
-
19. 如图,点是等边内一点,是外的一点, , , ≌ , , 连接 .
 (1)、求证:是等边三角形;(2)、当时,试判断的形状,并说明理由;(3)、探究:当为多少度时,是等腰三角形.20. 已知,如图①,在和中, , ,
(1)、求证:是等边三角形;(2)、当时,试判断的形状,并说明理由;(3)、探究:当为多少度时,是等腰三角形.20. 已知,如图①,在和中, , , (1)、求证:①;②;(2)、如图②,在和中, , , , 则AC与BD的等量关系为 . 的大小为 . (直接写出结果,不需要证明)21. 如图,A、B、C在同一条直线上,和均为等边三角形,、分别交、于点M、N,下列结论中:① , ② , ③ , ④ , ⑤平分 , 其中正确的有 . (填序号)
(1)、求证:①;②;(2)、如图②,在和中, , , , 则AC与BD的等量关系为 . 的大小为 . (直接写出结果,不需要证明)21. 如图,A、B、C在同一条直线上,和均为等边三角形,、分别交、于点M、N,下列结论中:① , ② , ③ , ④ , ⑤平分 , 其中正确的有 . (填序号) 22. 如图,在和中,三点在同一条直线上,连接 . 以下四个结论中:①;②;③;④ , 正确的个数是( ).
22. 如图,在和中,三点在同一条直线上,连接 . 以下四个结论中:①;②;③;④ , 正确的个数是( ). A、1个 B、2个 C、3个 D、4个23. 综合与实践、数学模型可以用来解决一类问题,是数学应用基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
A、1个 B、2个 C、3个 D、4个23. 综合与实践、数学模型可以用来解决一类问题,是数学应用基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地. (1)、发现问题:如图1,在与中, , , , B , F , C三点在一条直线上,连接EF交AB于点D . 则线段与、的数量关系是 ▲ , 并说明理由.(2)、类比探究:如图2,在中, , 以AC为边,作 , 满足 , E为BC上一点,连接AE , , 连接 , 求证: .24. 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2 , D在线段BC上,E是线段AD上一点.现以CE为直角边,C为直角顶点,在CE的下方作等腰直角△ECF,连接BF.
(1)、发现问题:如图1,在与中, , , , B , F , C三点在一条直线上,连接EF交AB于点D . 则线段与、的数量关系是 ▲ , 并说明理由.(2)、类比探究:如图2,在中, , 以AC为边,作 , 满足 , E为BC上一点,连接AE , , 连接 , 求证: .24. 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2 , D在线段BC上,E是线段AD上一点.现以CE为直角边,C为直角顶点,在CE的下方作等腰直角△ECF,连接BF.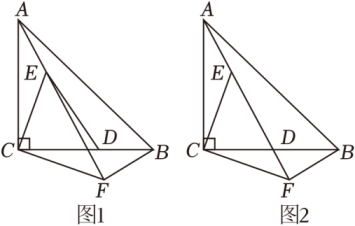 (1)、如图1,求证:∠CAE=∠CBF;(2)、当A、E、F三点共线时,如图2,
(1)、如图1,求证:∠CAE=∠CBF;(2)、当A、E、F三点共线时,如图2,①求证:∠DFB=90°;
②若BF=2,求AF的长.
七、半角模型(对角互补)
-
25. 如图,在四边形中,平分 , 且 , 若 , 则一定等于( )
 A、 B、 C、 D、26. 如图是正三角形,是顶角的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN .
A、 B、 C、 D、26. 如图是正三角形,是顶角的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN .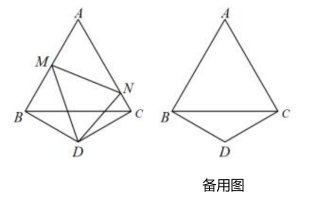 (1)、探究:写出线段BM、MN、NC之间的数量关系,并说明理由.(2)、若点M、N分别是AB、CA延长线上的点,其它条件不变,直接写出线段BM、MN、NC之间的数量关系(不用说明理由),并在图中画出图形.27. 我们定义:如图1,在四边形ABCD中,如果 , , 对角线BD平分 , 我们称这种四边形为“分角对补四边形”.
(1)、探究:写出线段BM、MN、NC之间的数量关系,并说明理由.(2)、若点M、N分别是AB、CA延长线上的点,其它条件不变,直接写出线段BM、MN、NC之间的数量关系(不用说明理由),并在图中画出图形.27. 我们定义:如图1,在四边形ABCD中,如果 , , 对角线BD平分 , 我们称这种四边形为“分角对补四边形”. (1)、特例感知:如图1,在“分角对补四边形”ABCD中,当时,根据教材中一个重要性质直接可得 , 这个性质是;(填序号)
(1)、特例感知:如图1,在“分角对补四边形”ABCD中,当时,根据教材中一个重要性质直接可得 , 这个性质是;(填序号)①垂线段最短:②垂直平分线的性质;③角平分线的性质;④三角形内角和定理
(2)、猜想论证:如图2,当为任意角时,猜想DA与DC的数量关系,并给予证明;(3)、探究应用:如图3,在等腰中, , BD平分 ,求证:.
28. (1)、如图 , 在四边形中, , , 分别是边上的点,且 , 线段之间的关系是;(不需要证明)(2)、如图 , 在四边形中, , , 分别是边上的点,且 , ()中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)、如图 , 在四边形中, , , 分别是边延长线上的点,且 , ()中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.29.
(1)、如图 , 在四边形中, , , 分别是边上的点,且 , 线段之间的关系是;(不需要证明)(2)、如图 , 在四边形中, , , 分别是边上的点,且 , ()中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)、如图 , 在四边形中, , , 分别是边延长线上的点,且 , ()中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.29. (1)、【问题背景】如图1,点E、F分别在正方形的边、上, , 连接 , 则有 , 试说明理由;(2)、【迁移应用】如图2,四边形中, , , 点E、F分别在边、上, , 若 , 都不是直角,且 , 试探究、、之间的数量关系;(3)、【联系拓展】如图3,在中, , , 点D、E均在边上,且 , 猜想、、满足的等量关系.(直接写出结论,不需要证明).30.
(1)、【问题背景】如图1,点E、F分别在正方形的边、上, , 连接 , 则有 , 试说明理由;(2)、【迁移应用】如图2,四边形中, , , 点E、F分别在边、上, , 若 , 都不是直角,且 , 试探究、、之间的数量关系;(3)、【联系拓展】如图3,在中, , , 点D、E均在边上,且 , 猜想、、满足的等量关系.(直接写出结论,不需要证明).30. (1)、如图1,在四边形ABCD中,AB=AD , ∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , 线段EF、BE、FD之间的关系是;(不需要证明)(2)、如图2,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)、如图3,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
(1)、如图1,在四边形ABCD中,AB=AD , ∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , 线段EF、BE、FD之间的关系是;(不需要证明)(2)、如图2,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)、如图3,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.八、含30度直角三角形