吉林省白城市大安市三中、四中、五中2023-2024学年八年级上学期第三次月考试卷数学试题
试卷更新日期:2024-01-25 类型:月考试卷
一、选择题(每小题2分,共12分)
-
1. 若分式有意义,则x满足的条件是( )A、x≠0 B、x>0 C、x>2 D、x≠22. 下面有4个标志图案,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列各项计算结果是的是( )A、 B、 C、 D、4. 如图,已知∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件正确的是( )
3. 下列各项计算结果是的是( )A、 B、 C、 D、4. 如图,已知∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件正确的是( ) A、∠ABC=∠ABD B、∠BAC=∠BAD C、AC=AD D、BD⊥BC5. 如图,将边长相等的正方形、正五边形和正六边形摆放在平面上,则的度数是( )
A、∠ABC=∠ABD B、∠BAC=∠BAD C、AC=AD D、BD⊥BC5. 如图,将边长相等的正方形、正五边形和正六边形摆放在平面上,则的度数是( )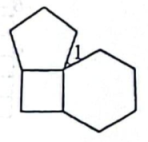 A、42° B、36° C、52° D、32°6. 如图,在△ABC中, ,CD AB于点D, ,AD=2,则BD=( )
A、42° B、36° C、52° D、32°6. 如图,在△ABC中, ,CD AB于点D, ,AD=2,则BD=( ) A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8二、填空题(每小题3分,共24分)
-
7. 分解因式: .8. 一个n边形的每个外角都等于36°,则n=.9. 引发春季传染病的某种病毒的直径是0.000000025米,将数据0.000000025用科学记数法表示为 .10. 计算: .11. 如图,在中, . 以点B为圆心,小于BC长为半径画弧,分别交边BA、BC于点M、N;再分别以点M、N为圆心,大于长为半径画弧,两弧交于点P,射线BP交AC于点D.则度数是 .
 12. A、B两地相距121千米,甲车和乙车的平均速度之比为4∶5,两车同时从A地出发到B地,乙车比甲车早到20分钟,求甲车的平均速度.若设甲车的平均速度为4x千米/小时,则所列方程是 .13. 如图,是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当的值最小时,度.
12. A、B两地相距121千米,甲车和乙车的平均速度之比为4∶5,两车同时从A地出发到B地,乙车比甲车早到20分钟,求甲车的平均速度.若设甲车的平均速度为4x千米/小时,则所列方程是 .13. 如图,是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当的值最小时,度. 14. 如图,在中, , AD是的平分线,延长AD至点E,使 , 连接BE,若的面积为9.则的面积是 .
14. 如图,在中, , AD是的平分线,延长AD至点E,使 , 连接BE,若的面积为9.则的面积是 .
三、解答题(每小题5分,共20分)
-
15. 计算:16. 解方程: .17. 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,求AC的长.
 18. 如图, . 求证: .
18. 如图, . 求证: .
四、解答题(每小题7分,共28分)
-
19. 先化简,再求值: , 其中 .20. 如图,在平面直角坐标系中,的各顶点坐标分别为 .
 (1)、画出关于x轴对称的;(2)、直接写出点的坐标.21. 如图,在等腰直角中, . 点D、E分别在AB、BC上,且 , , 连接DE、CD.
(1)、画出关于x轴对称的;(2)、直接写出点的坐标.21. 如图,在等腰直角中, . 点D、E分别在AB、BC上,且 , , 连接DE、CD.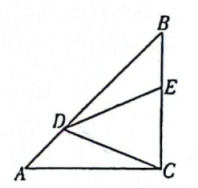 (1)、求证:;(2)、求的度数.22. 为了做好防疫工作,保障员工安全健康,某公司用400元购进一批某种型号的口罩.由于质量较好,公司又用600元购进第二批同一型号的口罩,已知第二批口罩的数量是第一批的2倍,且每包便宜5元,问第一批口罩每包的价格是多少元?公司前后两批一共购进多少包口罩?
(1)、求证:;(2)、求的度数.22. 为了做好防疫工作,保障员工安全健康,某公司用400元购进一批某种型号的口罩.由于质量较好,公司又用600元购进第二批同一型号的口罩,已知第二批口罩的数量是第一批的2倍,且每包便宜5元,问第一批口罩每包的价格是多少元?公司前后两批一共购进多少包口罩?五、解答题(每小题8分,共1.6分)
-
23. 如图是一个长为 , 宽为的长方形铁片,因工作需要,现将这个长方形铁片剪掉一个边长为的小正方形和一个长为 , 宽为bcm的小长方形,记铁片剩余部分的面积为S.
 (1)、用含a,b的式子表示S;(2)、当时,求S的值.24. 如图,在等边中,点D在边BC上,过点D作交AC于点E,过点E作 , 交BC的延长线于点F.
(1)、用含a,b的式子表示S;(2)、当时,求S的值.24. 如图,在等边中,点D在边BC上,过点D作交AC于点E,过点E作 , 交BC的延长线于点F.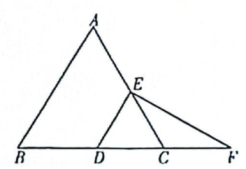 (1)、求的度数;(2)、求证: .
(1)、求的度数;(2)、求证: .六、解答题(每小题10分,共20分)
-
25. 如图
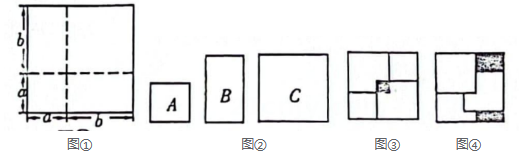 (1)、【操作】有若干张如图①所示的正方形纸片,将其沿虚线剪成如图②所示的A、B、C三类纸片 . 由图①可得到一个我们学习过的乘法公式,它是;(2)、【理解】用图②中的A、B、C三类纸片拼成一个两边长分别为和的长方形.求需要A、B、C三类纸片的张数,并画出拼出的长方形;(3)、【拓展】从图②中取出2张A型和1张C型纸片,将其中2张A型纸片放入到C型纸片内,如图③所示;再从图②中取出2张A型和1张C型纸片,将2张A型纸片放入到C型纸片内,如图④所示.若图④中的阴影部分图形的面积和比图③中的阴影部分图形的面积大 , 求a的值.26. 已知是等边三角形,是等腰三角形,点B、C在EF上,且 .
(1)、【操作】有若干张如图①所示的正方形纸片,将其沿虚线剪成如图②所示的A、B、C三类纸片 . 由图①可得到一个我们学习过的乘法公式,它是;(2)、【理解】用图②中的A、B、C三类纸片拼成一个两边长分别为和的长方形.求需要A、B、C三类纸片的张数,并画出拼出的长方形;(3)、【拓展】从图②中取出2张A型和1张C型纸片,将其中2张A型纸片放入到C型纸片内,如图③所示;再从图②中取出2张A型和1张C型纸片,将2张A型纸片放入到C型纸片内,如图④所示.若图④中的阴影部分图形的面积和比图③中的阴影部分图形的面积大 , 求a的值.26. 已知是等边三角形,是等腰三角形,点B、C在EF上,且 . (1)、如果和有公共的对称轴AH(如图①),求的度数;(2)、如果固定 , 转动 , 使AE与AB在一条直线上(如图②),那么EF与BC交于点M,EF与AC交于点N,求的度数,并说明的形状;(3)、如果继续转动 , 使AE与AH在一条直线上(如图③),EF与AC交于点D,请判断的形状,并说明理由.
(1)、如果和有公共的对称轴AH(如图①),求的度数;(2)、如果固定 , 转动 , 使AE与AB在一条直线上(如图②),那么EF与BC交于点M,EF与AC交于点N,求的度数,并说明的形状;(3)、如果继续转动 , 使AE与AH在一条直线上(如图③),EF与AC交于点D,请判断的形状,并说明理由.