江西省九江市永修县2023-2024学年九年级上学期12月月考数学试题

试卷更新日期：2024-01-25 类型：月考试卷

进入出卷网下载

一、单选题（本大题共6小题，每题3分，共18分，每小题只有一个正确选项）

1. 下列方程中是一元二次方程的是（）

A、 $x - \frac{1}{x} = 2$ B、 $x^{2} - 1 = 0$ C、 $a x^{2} + b x + c = 0$ D、 $3 x - 2 = 6$

查看试题解析
2. 如图所示的几何体的主视图是 $($ 　　 $)$

A、 B、 C、 D、

查看试题解析
3. 如图， $△ A B C$ 中， $A B = A C$ ， $B C = B D$ ， $A D = D E = E B$ ，则 $∠ A$ 的度数为（）

A、 $55 °$ B、 $45 °$ C、 $36 °$ D、 $30 °$

查看试题解析
4. 如图，在平面直角坐标系中，已知点E(−4，2)，F(−1，−1).以原点O为位似中心，把△EFO扩大到原来的2倍，则点E的对应点E′的坐标为（）

A、(−8，4) B、(8，−4) C、(8，4)或(−8，−4) D、(−8，4)或(8，−4)

查看试题解析
5. 如图，在正方形ABCD中，AB＝2，E是AD中点，BE交AC于点F ， DF的长为（）

A、 $\frac{5}{2}$ B、 $\sqrt{5}$ C、 $\frac{2 \sqrt{5}}{3}$ D、 $\frac{4 \sqrt{5}}{3}$

查看试题解析
6. 如图，顺次连接 $△ A B C$ 三边的中点D，E，F得到的三角形面积为 $S_{1}$ ，顺次连接 $△ C E F$ 三边的中点M，G，H得到的三角形面积为 $S_{2}$ ，顺次连接 $△ C G H$ 三边的中点得到的三角形面积为 $S_{3}$ ，设 $△ A B C$ 的面积为64，则 $S_{1} + S_{2} + S_{3} =$ （）

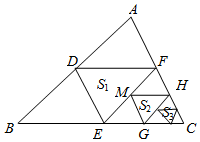A、21 B、24 C、27 D、32

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

7. 若 $\frac{a}{b}$ ＝ $\frac{c}{d}$ ＝ $\frac{2}{5}$ （b＋d $\neq$ 0），则 $\frac{a + c}{b + d}$ ＝．

查看试题解析
8. 已知△ABC∽△DEF ，且AB：DE＝1：2，则△ABC的面积与△DEF的面积之比为．

查看试题解析
9. 在反比例函数 $y = \frac{1 - k}{x}$ 的图象每一条分支上， $y$ 都随的增大而增大，则k的取值范围是．

查看试题解析
10. 在一个不透明的袋子里装有红球和白球共30个，这些球除颜色外都相同，小明通过多次试验发现，摸出白球的频率稳定在0.3左右，则袋子里白球可能是个．

查看试题解析
11. 若，是方程 $2 x^{2} + 4 x - 3 = 0$ 的两根，则 $a^{2} + a b - 2 b$ ．

查看试题解析
12. 如图，AB、CD都是BD的垂线，AB=4，CD=6，BD=14，P是BD上一点，联结AP、CP，所得两个三角形相似，则BP的长是。

查看试题解析

三、（本大题共5小题，每小题6分，共30分）

13.

(1)、解方程： $x^{2} + 4 x - 2 = 0$ ；

(2)、如图， $E$ ， $F$ 分别是矩形 $A B C D$ 的边 $A B$ ， $C D$ 上的一点，且 $D F = B E$ ．求证： $A F = C E$ ．

查看试题解析
14. 已知关于x的一元二次方程 $x^{2} - 2 (a - 1) x + a^{2} - a - 2 = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ ．

(1)、求a的取值范围；

(2)、若 $x_{1}$ ， $x_{2}$ 满足 $x_{1}^{2} + x_{2}^{2} - x_{1} x_{2} = 16$ ，求a的值．

查看试题解析
15. 将如图所示的牌面数字分别是1，2，3，4的四张扑克牌背面朝上，洗匀后放在桌面上．

(1)、从中随机抽出一张牌，牌面数字小于3的概率是；

(2)、先从中随机抽出一张牌不放回，将牌面数字作为十位上的数字，然后再随机抽取一张，将牌面数字作为个位上的数字，请用画树状图或列表的方法求组成的两位数恰好是3的倍数的概率．

查看试题解析
16. 已知函数 $y = y_{1} - y_{2}$ ，其中 $y_{1}$ 与x成正比例， $y_{2}$ 与 $x - 2$ 成反比例，且当 $x = 1$ 时， $y = 1$ ；当 $x = 3$ 时， $y = 5$ ．求 $y$ 关于x的函数解析式．

查看试题解析
17. 如图是 $4 \times 4$ 的正方形网格，请仅用无刻度的直尺按要求完成以下作图（保留作图痕迹）．

(1)、在图1中作 $∠ A B C$ 的角平分线；

(2)、在图2中过点 $C$ 作一条直线，使点 $A$ ， $B$ 到直线的距离相等．

查看试题解析

四、（本大题共3小题，每小题8分，共24分）

18. 如图，已知 $A (1 ， m)$ 、 $B (5 ， 1)$ 是一次函数 $y_{1} = k x + b$ 的图像和反比例函数 $y_{2} = \frac{a}{x}$ 的图像的两个交点．

(1)、求反比例函数和一次函数的解析式并在平面直角坐标系中画出图像；

(2)、连接 $A O 、 B O$ ，求 $△ A B O$ 的面积；

(3)、直接写出 $y_{2} \geq y_{1}$ 时x的取值范围．

查看试题解析
19. 便民水泥代销点销售某种水泥，每吨进价为250元，如果每吨销售价定为290元时，平均每天可售出16吨.

(1)、若代销点采取降低售价促销的方式，试求每吨的销售利润y（元）与每吨降低x（元）之间的函数关系式；

(2)、若每吨售价每降低5元，则平均每天能多售出4吨，问：每吨水泥的实际售价定为多少元时，每天的销售利润平均可达720元.

查看试题解析
20. 我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳，如图是小然站在地面 $M N$ 欣赏悬挂在墙壁 $P M$ 上的油画 $A D$ （ $P M ⊥ M N$ ）的示意图，设油画 $A D$ 与墙壁的夹角 $∠ P A D = a$ ，此时小然的眼睛与油画底部 $A$ 处于同一水平线上，视线恰好落在油画的中心位置 $E$ 处，且与 $A D$ 垂直．已知油画的长度 $A D$ 为 $100 c m$ ．

(1)、视线 $∠ A B D$ 的度数为；（用含的式子表示）

(2)、当小然到墙壁 $P M$ 的距离 $A B = 250 c m$ 时，求油画顶部点 $D$ 到墙壁 $P M$ 的距离；

(3)、当油画底部 $A$ 处位置不变，油画 $A D$ 与墙壁的夹角逐渐减小时，小然为了保证欣赏油画的视觉效果最佳，他应该更靠近墙壁 $P M$ ，还是不动或者远离墙壁 $P M$ ？（直接回答即可）

查看试题解析

五、（本大题共2小题，每小题9分，共18分）

21. 某医药研究所研制了一种新药，在试验药效时发现：成人按规定剂量服用后，检测到从第5分钟起每分钟每毫升血液中含药量增加0.2微克，第100分钟达到最高，接着开始衰退．血液中含药量y（微克）与时间x（分钟）的函数关系如图，并发现衰退时y与x成反比例函数关系．

(1)、 $a =$ ；

(2)、当 $5 \leq x \leq 100$ 时，y与x之间的函数关系式为；
当 $x > 100$ 时，y与x之间的函数关系式为；

(3)、如果每毫升血液中含药量不低于10微克时是有效的，求出一次服药后的有效时间多久？

查看试题解析
22. 如图，平行四边形 $A B C D$ 中， $A C$ 与 $B D$ 相交于点O ，点P为 $B C$ 中点， $A P$ 交 $B D$ 于点E ，连接 $C E$ ， $A E = C E$ ．

(1)、求证：平行四边形 $A B C D$ 为菱形；

(2)、若 $A B = 5$ ， $A E = 3$ ，
①求 $\frac{O E}{B E}$ 的值．
②求 $B D$ 的长．

查看试题解析

六、解答题本大题共12分

23.

(1)、课本再现
在证明“三角形内角和定理”时，小明只撕下三角形纸片的一个角拼成图1即可证明，其中与 $∠ A$ 相等的角是；

(2)、类比迁移
如图2，在四边形 $A B C D$ 中， $∠ A B C$ 与 $∠ A D C$ 互余，小明发现四边形 $A B C D$ 中这对互余的角可类比（1）中思路进行拼合：先作 $∠ C D F = ∠ A B C$ ，再过点 $C$ 作 $C E ⊥ D F$ 于点 $E$ ，连接 $A E$ ，发现 $A D$ ， $D E$ ， $A E$ 之间的数量关系是；

(3)、方法运用
如图3，在四边形 $A B C D$ 中，连接 $A C$ ， $∠ B A C = 90 °$ ，点 $O$ 是 $△ A C D$ 两边垂直平分线的交点，连接 $O A$ ， $∠ O A C = ∠ A B C$ ．
①求证： $∠ A B C + ∠ A D C = 90 °$ ；
②连接 $B D$ ，如图4，已知 $A D = m$ ， $D C = n$ ， $\frac{A B}{A C} = 2$ ，求 $B D$ 的长（用含 $m$ ，的式子表示）

查看试题解析