重庆市渝北区六校联盟2023-2024学年九年级上学期第二次大练兵(期中)数学试题
试卷更新日期:2024-01-25 类型:期中考试
一、选择题(本大题共10小题,每题4分,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的倒数是( )A、 B、 C、 D、2. 面对新冠病毒疫情,我国毫不动摇坚持动态清零总方针,外防输入,内防反弹,下面是支付宝“国案政务服务平台”中关于疫情防控的四个小程序图标,其中的图案既是轴对称图形,又是中心对称图形的是( )A、
 各地疫情风险等级查询
B、
各地疫情风险等级查询
B、 扫一扫防疫信息码
C、
扫一扫防疫信息码
C、 核酸和抗体检测查询
D、
核酸和抗体检测查询
D、 医用口罩信息查询
3. 下列是一元二次方程的是( )A、 B、 C、 D、4. 在平面直角坐标系中,以原点为圆心,为半径作圆,点的坐标是 , 则点与的位置关系是( )A、点在内 B、点在外 C、点在上 D、点在上或在外5. 方程的根的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个负实数根 D、有两个正实数根6. 估计的值应在( )A、和之间 B、和之间 C、和之间 D、和之间7. 用围棋子按下面的规律摆放图形,则摆放第个图形需要围棋子的枚数是( )
医用口罩信息查询
3. 下列是一元二次方程的是( )A、 B、 C、 D、4. 在平面直角坐标系中,以原点为圆心,为半径作圆,点的坐标是 , 则点与的位置关系是( )A、点在内 B、点在外 C、点在上 D、点在上或在外5. 方程的根的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个负实数根 D、有两个正实数根6. 估计的值应在( )A、和之间 B、和之间 C、和之间 D、和之间7. 用围棋子按下面的规律摆放图形,则摆放第个图形需要围棋子的枚数是( ) A、 B、 C、 D、8. 如图,是的外接圆,已知 , 则的大小为( )
A、 B、 C、 D、8. 如图,是的外接圆,已知 , 则的大小为( ) A、 B、 C、 D、9. 若整数使得关于的分式方程有正整数解,且使关于的不等式组至少有个整数解,那么符合条件的所有整数的和为( )A、 B、 C、 D、10. 二次函数的图象如图所示,下列结论:
A、 B、 C、 D、9. 若整数使得关于的分式方程有正整数解,且使关于的不等式组至少有个整数解,那么符合条件的所有整数的和为( )A、 B、 C、 D、10. 二次函数的图象如图所示,下列结论:
;
;
为任意实数时,;
;
若 , 且 , 则其中正确的有( )
A、个 B、个 C、个 D、个二、填空题(本大题共8小题,每题4分,共32.0分)
-
11. .12. 如图, , 是的切线, , 是切点,若 , 则 .
 13. 节约是一种美德,节约是一种智慧.据不完全统计,全国每年浪费食物总量折合粮食可养活约3亿5千万人,350000000用科学记数法表示为 .14. 二次函数的顶点坐标是 .15. 三角形两边的长是和 , 第三边的长是方程的根,则该三角形的周长为 .16. 如图,菱形的边长为 , , 是以点为圆心,长为半径的弧,是以点为圆心,长为半径的弧,则阴影部分的面积为结果保留根号
13. 节约是一种美德,节约是一种智慧.据不完全统计,全国每年浪费食物总量折合粮食可养活约3亿5千万人,350000000用科学记数法表示为 .14. 二次函数的顶点坐标是 .15. 三角形两边的长是和 , 第三边的长是方程的根,则该三角形的周长为 .16. 如图,菱形的边长为 , , 是以点为圆心,长为半径的弧,是以点为圆心,长为半径的弧,则阴影部分的面积为结果保留根号 17. 如图,是等边三角形内一点,将线段绕点顺时针旋转得到线段 , 连结若 , , , 则四边形的面积为 .
17. 如图,是等边三角形内一点,将线段绕点顺时针旋转得到线段 , 连结若 , , , 则四边形的面积为 .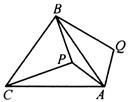 18. 若定义一种新运算: , 例如:@ , @下列说法:(1)、@;(2)、@与直线为常数有个交点,则的取值范围是 .
18. 若定义一种新运算: , 例如:@ , @下列说法:(1)、@;(2)、@与直线为常数有个交点,则的取值范围是 .三、计算题(本大题共2小题,共18.0分)
-
19. 计算:(1)、;(2)、20. 先化简,再求值: , 其中 , .
四、解答题(本大题共6小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
-
21. 如图,在四边形中, , 连接 , .
 (1)、尺规作图:作线段的垂直平分线交于点 , 交于点 ,
(1)、尺规作图:作线段的垂直平分线交于点 , 交于点 ,连接不写作法,保留作图痕迹;
(2)、在所作图中,证明四边形为菱形,完成下列填空.证明:垂直平分
.
,
即
四边形是 .
.
四边形为菱形.
22. 随着寒冬的来临,“新冠”疫情再次肆虐,某中学为让学生了解“新冠病毒”传染情况,增强学生的防护意识,开展了“远离新冠珍爱生命”的防“新冠”安全知识测试活动,现从学校八、九年级中各随机抽取名学生的测试成绩满分分,分及分以上为优秀进行整理、描述和分析,下面给出了部分信息:八年级名学生的测试成绩是: , , , , , , , , , , , , , , .

八、九年级抽取的学生的测试成绩的平均数、众数、中位数、分及以上人数所占百分比如表所示:年级
平均数
众数
中位数
分及以上人数所占百分比
八年级
九年级
九年级名学生的测试成绩条形统计图如图示.
根据以上信息,解答下列问题:
(1)、上述表中的 , , ;(2)、根据以上数据,你认为该校八、九年级中哪个年级学生掌握防“新冠”安全知识更好?请说明理由一条即可: .(3)、该中学八年级有名、九年级有名学生参加了此次测试活动,估计参加此次测试活动获得成绩优秀的学生人数是多少?23. 又到了脐橙丰收季,某水果超市老板发现今年奉节脐橙和赣南脐橙很受欢迎,今年月第一周购进奉节脐橙和赣南脐橙两个品种,已知千克赣南脐橙的进价比千克奉节脐橙的进价多元,购买千克赣南脐橙的价格与购买千克奉节脐橙的价格相同.(1)、今年月第一周每千克奉节脐橙和赣南脐橙的进价分别是多少元?(2)、今年月第一周,水果超市老板以元每千克售出奉节脐橙千克,元每千克售出赣南脐橙千克;第二周水果超市老板又以第一周的价格购进一批奉节脐橙和赣南脐橙,为促进奉节脐橙的销量,该水果超市老板决定调整价格,每千克奉节脐橙的售价在第一周的基础上下降元,每千克赣南脐橙的售价不变,由于此批奉节脐橙品质较好又便宜,第二周奉节脐橙的销量比第一周增加了千克,而赣南脐橙的销量比第一周减少了千克,最终该水果超市第二周销售两种脐橙总共获利元,求的值.24. 有这样一个问题:探究函数的图象与性质.小明根据学习函数的经验,对函数的图象与性质进行了探究.
(1)、函数的自变量的取值范围是;(2)、下表是与的几组对应值,请你求的值;(3)、如图,在平面直角坐标系中,描出了以上表中各组数值所对应的点,请你画出该函数的图象; (4)、结合函数的图象,写出该函数的一条性质: .25. 如图 , 在平面直角坐标系中,抛物线经过 , 与轴交于点 , 经过点的直线与抛物线交于另一点 , 点为抛物线的顶点,抛物线的对称轴与轴交于点 .
(4)、结合函数的图象,写出该函数的一条性质: .25. 如图 , 在平面直角坐标系中,抛物线经过 , 与轴交于点 , 经过点的直线与抛物线交于另一点 , 点为抛物线的顶点,抛物线的对称轴与轴交于点 . (1)、求直线的解析式;(2)、如图 , 点为直线上方抛物线上一动点,连接 , 当的面积最大时,求点的坐标以及面积的最大值.(3)、如图 , 将点右移一个单位到点 , 连接 , 将中抛物线沿射线平移得到新抛物线 , 经过点 , 的顶点为点 , 在新抛物线的对称轴上是否存在点 , 使得是等腰三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.26. 在中, , , 为边上一点,连接 .
(1)、求直线的解析式;(2)、如图 , 点为直线上方抛物线上一动点,连接 , 当的面积最大时,求点的坐标以及面积的最大值.(3)、如图 , 将点右移一个单位到点 , 连接 , 将中抛物线沿射线平移得到新抛物线 , 经过点 , 的顶点为点 , 在新抛物线的对称轴上是否存在点 , 使得是等腰三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.26. 在中, , , 为边上一点,连接 .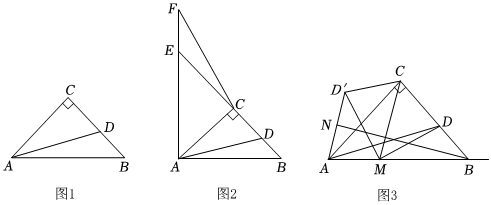 (1)、如图 , 若 , , 求的长;(2)、如图 , 将的边绕点在同一平面内顺时针旋转得到 , 为延长线上一点,连接若 , , 求证:;(3)、如图 , 在的条件下,为射线上一动点,连接 , , 将沿翻折,得到 , 连接 , 为的中点,连接 , 当的长度最小时,请直接写出的值.
(1)、如图 , 若 , , 求的长;(2)、如图 , 将的边绕点在同一平面内顺时针旋转得到 , 为延长线上一点,连接若 , , 求证:;(3)、如图 , 在的条件下,为射线上一动点,连接 , , 将沿翻折,得到 , 连接 , 为的中点,连接 , 当的长度最小时,请直接写出的值.