北京市房山区2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-01-25 类型：期末考试

进入出卷网下载

一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个.

1. 下列图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如果 $\frac{x}{y} = \frac{5}{3}$ ，那么 $\frac{x - y}{y}$ 的值是（）

A、 $- \frac{5}{2}$ B、 $- \frac{2}{3}$ C、 $\frac{2}{3}$ D、 $\frac{5}{2}$

查看试题解析
3. 抛物线 $y = {(x - 1)}^{2} + 2$ 的顶点坐标是（）

A、 $(- 1 ， 2)$ B、 $(1 ， 2)$ C、 $(- 1 ， - 2)$ D、 $(1 ， - 2)$

查看试题解析
4. 如图，在 $⊙ O$ 中，若 $∠ B A C = 25 °$ ，则 $∠ B O C$ 的度数是（）

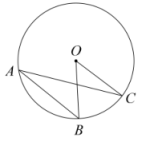A、15° B、25° C、50° D、75°

查看试题解析
5. 将二次函数 $y = x^{2}$ 的图象向上平移5个单位，得到的函数图象的表达式是（）

A、 $y = x^{2} + 5$ B、 $y = x^{2} - 5$ C、 $y = {(x + 5)}^{2}$ D、 $y = {(x - 5)}^{2}$

查看试题解析
6. 若点 $A (1 ， y_{1})$ ， $B (2 ， y_{2})$ 在反比例函数 $y = - \frac{2}{x}$ 的图象上，则 $y_{1}$ ， $y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} \geq y_{2}$ D、 $y_{1} \leq y_{2}$

查看试题解析
7. 如图，建筑物CD和旗杆AB的水平距离BD为9m，在建筑物的顶端C测得旗杆顶部A的仰角 $α$ 为30°，旗杆底部B的俯角 $β$ 为45°，则旗杆AB的高度为（）

A、 $3 \sqrt{2} m$ B、 $3 \sqrt{3} m$ C、 $(3 \sqrt{2} + 9) m$ D、 $(3 \sqrt{3} + 9) m$

查看试题解析
8. 如图，AB是半圆O的直径，半径 $O C ⊥ A B$ ，点D是 $\overset{⌢}{B C}$ 的中点，连接BD ， OD ， AC ， AD ， AD与OC交于点E ，给出下面三个结论：
①AD平分 $∠ C A B$ ；② $A C ∥ O D$ ；③ $A E = \sqrt{2} D E$ .
上述结论中，所有正确结论的序号是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题（共16分，每题2分）

9. 函数y= $\frac{1}{x - 1}$ 的自变量x的取值范围是。

查看试题解析
10. 如图，四边形ABCD内接于 $⊙ O$ ，若 $∠ C = 130 °$ ，则 $∠ A =$ .

查看试题解析
11. 请写出一个图象过点 $(1 ， 2)$ 的函数表达式：.

查看试题解析
12. 如图，在 $△ A B C$ 中，点D ， E分别在AB ， AC上， $D E ∥ B C$ ， $D E = 3$ ， $B C = 9$ ， $A E = 2$ ，则EC的长为.

查看试题解析
13. 如图，A ， B ， D三点在半径为5的 $⊙ O$ 上，AB是 $⊙ O$ 的一条弦，且 $O D ⊥ A B$ 于点C ，若 $A B = 8$ ，则OC的长为.

查看试题解析
14. 如图，在33的方格中，每个小方格都是边长为1的正方形，O ， A ， B分别是小正方形的顶点，点C在OB上，则 $\overset{⌢}{A C}$ 的长为.

查看试题解析
15. 在 $△ A B C$ 中， $B C = 2$ ， $A C = 2 \sqrt{3}$ ， $∠ A = 30 °$ ，则 $△ A B C$ 的面积为.

查看试题解析
16. 在平面直角坐标系 $x O y$ 中，A为y轴正半轴上一点.已知点 $B (1 ， 0)$ ， $C (5 ， 0)$ ， $⊙ P$ 是 $△ A B C$ 的外接圆.
⑴点P的横坐标为；
⑵若 $∠ B A C$ 最大时，则点A的坐标为.

查看试题解析

三、解答题（共68分，第17-22题，每题5分，第23-26题，每题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程..

17. 计算： $4 s i n 45 ° + {(\sqrt{3} - 1)}^{0} + | - 5 | - \sqrt{8}$ .

查看试题解析
18. 如图，D ， E分别是 $△ A B C$ 的边AB ， AC上的点， $∠ A D E = ∠ C$ .
求证： $△ A D E ∽ △ A C B$ .

查看试题解析
19. 已知二次函数 $y = x^{2} + 2 x - 3$ .

(1)、在平面直角坐标系中画出它的图象，并写出它的对称轴；

(2)、结合图象直接写出当 $- 1 < x < 1$ 时， $y$ 的取值范围.

查看试题解析
20. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = 5$ ， $A B = 13$ .求 $c o s A$ 的值.

查看试题解析
21. 已知：如图 $⊙ O$ .
求作： $⊙ O$ 的内接正方形.
作法：①作 $⊙ O$ 的直径AB；
②作直径AB的垂直平分线MN交 $⊙ O$ 于点C ， D；
③连接AC ， BC ， AD ， BD.
所以四边形ACBD就是所求作的正方形.

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明.
证明：∵MN是AB的垂直平分线，
∴MN过点O.
∴ $∠ A O C = ∠ C O B = ∠ B O D = ∠ D O A = 90 °$ .
∴ $A C = B C = B D = A D$ .（）（填推理的依据）
∴四边形ACBD是菱形.
∵AB是 $⊙ O$ 的直径，
∴ $∠ A C B =$ °.（）（填推理的依据）
∴菱形ACBD是正方形.

查看试题解析
22. 如图，在矩形ABCD中，AC为对角线， $D E ⊥ A C$ ，垂足为点E.

(1)、求证： $∠ D A E = ∠ E D C$ ；

(2)、若 $B C = 8$ ， $t a n ∠ E D C = \frac{3}{4}$ ，求 $D E$ 的长.

查看试题解析
23. 在平面直角坐标系 $x O y$ 中，直线 $y = x$ 与双曲线 $y = \frac{k}{x}$ 相交于点 $P (2 ， m)$ 和点Q.

(1)、求m的值及点Q的坐标；

(2)、已知点 $N (0 ， n)$ ，过点N作平行于x轴的直线交直线 $y = x$ 与双曲线 $y = \frac{k}{x}$ 分别为点 $A (x_{1} ， y_{1})$ 和 $B (x_{2} ， y_{2})$ .当 $x_{1} > x_{2}$ 时，直接写出 $n$ 的取值范围是.

查看试题解析
24. 如图，AB是 $⊙ O$ 的直径，AC ， BC是弦，点D在AB的延长线上，且 $∠ D C B = ∠ D A C$ ， $⊙ O$ 的切线AE与DC的延长线交于点E.

(1)、求证：CD是 $⊙ O$ 的切线；

(2)、若 $⊙ O$ 的半径为2， $∠ D = 30 °$ ，求AE的长.

查看试题解析
25. 原地正面掷实心球是北京市初中学业水平考试体育现场考试的选考项目之一.实心球被掷出后的运动路线可以看作是抛物线的一部分，建立如图所示的平面直角坐标系.实心球从出手（点A处）到落地的过程中，实心球的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系 $y = a {(x - h)}^{2} + k (a < 0)$ .
九年级一名男生进行了两次训练.

(1)、第一次训练时，实心球的水平距离x与竖直高度y的几组数据如下：
水平距离x/m
0
3
5
6
7
9
竖直高度y/m
2
$\frac{17}{4}$
$\frac{59}{12}$
5
$\frac{59}{12}$
$\frac{17}{4}$
根据上述数据，直接写出实心球竖直高度的最大值，并求出满足的函数关系 $y = a {(x - h)}^{2} + k (a < 0)$ ；

(2)、第二次训练时，实心球的竖直高度y与水平距离x近似满足函数关系 $y = - \frac{1}{12} {(x - 5)}^{2} + \frac{49}{12}$ .记该男生第一次训练实心球落地的水平距离为 $d_{1}$ ，第二次训练实心球落地的水平距离为 $d_{2}$ ，则 $d_{1}$ $d_{2}$ （填“>”“=”或“<”）.

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，点 $(1 ， m)$ ， $(3 ， n)$ ，在抛物线 $y = a x^{2} + b x + 4 (a > 0)$ 上，设抛物线的对称轴为 $x = t$ .

(1)、当 $m = n$ 时，求抛物线与y轴交点的坐标及t的值；

(2)、点 $(x_{0} ， n) (x_{0} \neq 3)$ ，在抛物线上，若 $m < n < 4$ ，求t的取值范围及 $x_{0}$ 的取值范围.

查看试题解析
27. 如图，在等边三角形ABC中，E ， F分别是BC ， AC上的点，且 $B E = C F$ ， AE ， BF交于点G.

(1)、 $∠ A G F =$ °；

(2)、过点A作 $A D ∥ B C$ （点D在AE的右侧），且 $A D = B C$ ，连接DG.
①依题意补全图形；
②用等式表示线段AG ， BG与DG的数量关系，并证明.

查看试题解析
28. 定义：在平面直角坐标系xOy中，对于 $⊙ M$ 内的一点P ，若在 $⊙ M$ 外存在点 $P^{'}$ ，使得 $M P^{'} = 2 M P$ ，则称点P为 $⊙ M$ 的“内二分点”.

(1)、当 $⊙ O$ 的半径为2时，
①在 $P_{1} (- 1 ， 0)$ ， $P_{2} (1 ， \frac{3}{2})$ ， $P_{3} (\sqrt{2} ， - 1)$ ， $P_{4} (- \sqrt{3} ， - 1)$ 四个点中，是 $⊙ O$ 的“内二分点”的是 ▲ ；
②已知一次函数 $y = k x - 2 k$ 在第一象限的图象上的所有点都是 $⊙ O$ 的“内二分点”，求k的取值范围；

(2)、已知点 $M (m ， 0)$ ， $B (0 ， - 1)$ ， $C (1 ， - 1)$ ， $⊙ M$ 的半径为4，若线段BC上存在 $⊙ M$ 的“内二分点”，直接写出m的取值范围.

查看试题解析

水平距离x/m	0	3	5	6	7	9
竖直高度y/m	2	$\frac{17}{4}$	$\frac{59}{12}$	5	$\frac{59}{12}$	$\frac{17}{4}$