备战2024年中考数学细点逐一突破真题训练第15章圆
试卷更新日期:2024-01-25 类型:一轮复习
一、圆的基本概念及定义
-
1. 下列说法中正确的是( )A、平分弦的直径垂直于弦 B、圆心角是圆周角的2倍 C、三角形的外心到三角形各边的距离相等 D、从圆外一点可以引圆的两条切线,这一点和圆心的连线平分两条切线的夹角2. 下列命题中,不正确的是( )A、一个点到圆心的距离大于这个圆的半径,则这个点在圆外 B、一条直线垂直于圆的半径,那么这条直线是圆的切线 C、两个圆的圆心距等于它们的半径之和,则这两圆外切 D、圆心到一条直线的距离小于这个圆的半径,则这条直线与圆有两个交点3. 下列四个图中,∠x是圆周角的是( )A、
 B、
B、 C、
C、 D、
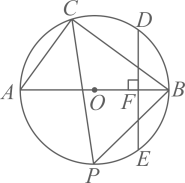
D、 4. 下列语句中:①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等,不正确的有( )A、2个 B、3个 C、4个 D、5个5. 如图,已知正方形 , 以点为圆心,长为半径作 , 点与的位置关系为( )
4. 下列语句中:①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等,不正确的有( )A、2个 B、3个 C、4个 D、5个5. 如图,已知正方形 , 以点为圆心,长为半径作 , 点与的位置关系为( ) A、点在外 B、点在内 C、点在上 D、无法确定6. (多选)如图,已知锐角∠AOB , 按如下步骤作图:(1)在射线OA上取一点C , 以点O为圆心,OC长为半径作 , 交射线OB于点D , 连接CD;(2)分别以点C , D为圆心,CD长为半径作弧,交于点M , N;③连接OM , MN , ND . 根据以上作图过程及所作图形,下列结论中正确的是( )
A、点在外 B、点在内 C、点在上 D、无法确定6. (多选)如图,已知锐角∠AOB , 按如下步骤作图:(1)在射线OA上取一点C , 以点O为圆心,OC长为半径作 , 交射线OB于点D , 连接CD;(2)分别以点C , D为圆心,CD长为半径作弧,交于点M , N;③连接OM , MN , ND . 根据以上作图过程及所作图形,下列结论中正确的是( ) A、∠COM=∠COD B、若OM=MN , 则∠AOB=20° C、MN∥CD D、∠COD=3∠MND
A、∠COM=∠COD B、若OM=MN , 则∠AOB=20° C、MN∥CD D、∠COD=3∠MND二、圆周角定理及其推论
-
7. 如图,正五边形内接于 , 连接 , 则( )
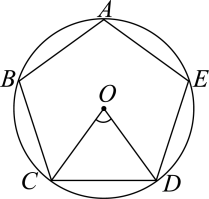 A、 B、 C、 D、8. 如图,A,B,C为上的三个点, , 若 , 则的度数是( )
A、 B、 C、 D、8. 如图,A,B,C为上的三个点, , 若 , 则的度数是( )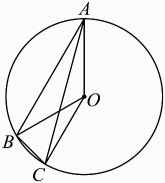 A、 B、 C、 D、12°9. 如图,四边形是的内接四边形, , . 若的半径为5,则的长为( )
A、 B、 C、 D、12°9. 如图,四边形是的内接四边形, , . 若的半径为5,则的长为( )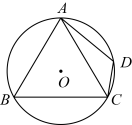 A、 B、 C、 D、10. 如图,点O是外接圆的圆心,点I是的内心,连接 , . 若 , 则的度数为( )
A、 B、 C、 D、10. 如图,点O是外接圆的圆心,点I是的内心,连接 , . 若 , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、三、垂径定理及其推论
-
11. 已知 的直径 , 是 的弦, ,垂足为 ,且 ,则 的长为( )A、 B、 C、 或 D、 或12. 已知 的直径 是 的弦, , 垂足为 , 且 , 则 的度数为 ( )A、30° B、60° C、30°或60° D、45°或60°13. 下列命题正确的是( )A、在一个三角形中至少有两个锐角 B、在圆中,垂直于弦的直径平分弦 C、如果两个角互余,那么它们的补角也互余 D、两条直线被第三条直线所截,同位角一定相等14. 沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图.是以O为圆心,为半径的圆弧,C是弦的中点,D在上, . “会圆术”给出长l的近似值s计算公式: , 当 , 时, . (结果保留一位小数)
 15. 陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一图是从正面看到的一个“老碗”图的形状示意图.是的一部分,是的中点,连接 , 与弦交于点 , 连接 , 已知 , 碗深 , 则的半径为( )
15. 陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一图是从正面看到的一个“老碗”图的形状示意图.是的一部分,是的中点,连接 , 与弦交于点 , 连接 , 已知 , 碗深 , 则的半径为( ) A、 B、 C、 D、
A、 B、 C、 D、四、圆与锐角三角函数
-
16. 如图,中, , , , 以为直径作 , 交于点F,连接并延长,分别交于D、E两点,连接、 .
 (1)、求证:是的切线;(2)、求证:;(3)、求的正切值.17. 如图,为的直径,C,D为上两点,连接 , , , , 线段与相交于点E,过点D作 , 交的延长线于点F.
(1)、求证:是的切线;(2)、求证:;(3)、求的正切值.17. 如图,为的直径,C,D为上两点,连接 , , , , 线段与相交于点E,过点D作 , 交的延长线于点F. (1)、求证:是的切线;(2)、若 , , , 求的半径.18. 如图,点D , E在以为直径的上,的平分线交于点B , 连接 , , , 过点E作 , 垂足为H , 交于点F .
(1)、求证:是的切线;(2)、若 , , , 求的半径.18. 如图,点D , E在以为直径的上,的平分线交于点B , 连接 , , , 过点E作 , 垂足为H , 交于点F . (1)、求证:;(2)、若 , 求的长.19. 如图,在边长为1的正方形网格中,⊙O是△ABC的外接圆,点A,B,O在格点上,则cos∠ACB的值是 .
(1)、求证:;(2)、若 , 求的长.19. 如图,在边长为1的正方形网格中,⊙O是△ABC的外接圆,点A,B,O在格点上,则cos∠ACB的值是 .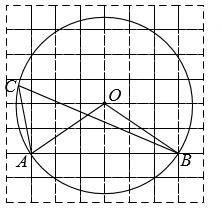 20. 如图,已知是的直径,直线是的切线,切点为 , , 垂足为 . 连接 .
20. 如图,已知是的直径,直线是的切线,切点为 , , 垂足为 . 连接 . (1)、求证:平分;(2)、若 , , 求的半径.
(1)、求证:平分;(2)、若 , , 求的半径.五、阿氏圆、隐含圆问题
-
21. 已知,在中, , 垂足分别为相交于点 , 则的长度的最大值为( )A、2 B、 C、1 D、22. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点Р是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值为( )
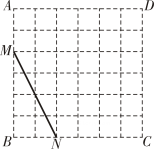 A、 B、6 C、 D、23. 如图,的半径为2,圆心M的坐标为 , 点P是上的任意一点, , 且与x轴分别交于A、B两点,若点A、点B关于原点O对称,则的最大值为( )
A、 B、6 C、 D、23. 如图,的半径为2,圆心M的坐标为 , 点P是上的任意一点, , 且与x轴分别交于A、B两点,若点A、点B关于原点O对称,则的最大值为( ) A、9 B、10 C、12 D、14
A、9 B、10 C、12 D、14六、圆阴影面积
-
24. 如图,为的直径,为上一点,为延长线上一点, , 的半径为5.
 (1)、求证:为的切线;(2)、若 , 求图中阴影部分的面积(结果保留);(3)、若 , 求的长.25. 如图,是等腰直角三角形, , 以BC为直径作交斜边AB于点D,点M是中点,过点M作直线于点E,交AC于点F.
(1)、求证:为的切线;(2)、若 , 求图中阴影部分的面积(结果保留);(3)、若 , 求的长.25. 如图,是等腰直角三角形, , 以BC为直径作交斜边AB于点D,点M是中点,过点M作直线于点E,交AC于点F. (1)、证明:EF是的切线;(2)、若 , 求图中阴影部分面积.26. 如图,是的外接圆,半径为4,连接OB,OC,OA,若 , , 则阴影部分的面积是( )
(1)、证明:EF是的切线;(2)、若 , 求图中阴影部分面积.26. 如图,是的外接圆,半径为4,连接OB,OC,OA,若 , , 则阴影部分的面积是( ) A、 B、 C、 D、27. 如图,某玩具品牌的标志由半径为的三个等圆构成,且三个等圆相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
A、 B、 C、 D、27. 如图,某玩具品牌的标志由半径为的三个等圆构成,且三个等圆相互经过彼此的圆心,则图中三个阴影部分的面积之和为( ) A、 B、 C、 D、28. 如图,在△ABC中,∠ABC=90°,∠ACB=30°,AB=4,点O为BC的中点,以O为圆心,OB长为半径作半圆,交AC于点D,则图中阴影部分的面积是( )
A、 B、 C、 D、28. 如图,在△ABC中,∠ABC=90°,∠ACB=30°,AB=4,点O为BC的中点,以O为圆心,OB长为半径作半圆,交AC于点D,则图中阴影部分的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、七、圆切线相关证明
-
29. 如图,的半径是 , AB是的直径,半径于点O,点E是半径上一点,交于点D,且.
 (1)、求证:是的切线;(2)、若 , 求:和的长.30. 如图,是的直径, , 的弦于点 , . 过点作的切线交的延长线于点 , 连接 .
(1)、求证:是的切线;(2)、若 , 求:和的长.30. 如图,是的直径, , 的弦于点 , . 过点作的切线交的延长线于点 , 连接 . (1)、求证:平分;(2)、为上一点,连接交于点 , 若 , 求的长.31. 已知内接于 , 点D是上一点.
(1)、求证:平分;(2)、为上一点,连接交于点 , 若 , 求的长.31. 已知内接于 , 点D是上一点. (1)、如图①,若为的直径,连接 , 求和的大小;(2)、如图②,若// , 连接 , 过点D作的切线,与的延长线交于点E,求的大小.32. 如图1,已知是的内接三角形,AB为直径, , D为上一点.
(1)、如图①,若为的直径,连接 , 求和的大小;(2)、如图②,若// , 连接 , 过点D作的切线,与的延长线交于点E,求的大小.32. 如图1,已知是的内接三角形,AB为直径, , D为上一点.图1
 图2
图2 (1)、当点D为的中点时,连接DB , DC , 求和的大小;(2)、如图2,过点D作的切线,与AB的延长线交于点P , 且 , 连接DC , OC , 求的大小.
(1)、当点D为的中点时,连接DB , DC , 求和的大小;(2)、如图2,过点D作的切线,与AB的延长线交于点P , 且 , 连接DC , OC , 求的大小.八、网格作图
-
33. 如图,由小正方形构成的6×6网格,每个小正方形的顶点叫做格点.⊙O经过A,B,C三个格点,仅用无刻度的直尺在给定网格中按要求画图.(保留作图痕迹)
 (1)、在图①中的圆上找一点D(不与点B重合),使∠ADC=90°;(2)、在图②中的圆上找一点E,使OE平分弧AB;(3)、在图③中的圆上找一点F,使AF平分∠BAC.34. 如图,在△ABC中,已知∠ABC=120°,AC=4,
(1)、在图①中的圆上找一点D(不与点B重合),使∠ADC=90°;(2)、在图②中的圆上找一点E,使OE平分弧AB;(3)、在图③中的圆上找一点F,使AF平分∠BAC.34. 如图,在△ABC中,已知∠ABC=120°,AC=4, (1)、用直尺和圆规作出△ABC的外接圆⊙O (不写作法,保留作图痕迹);(2)、求∠AOC的度数;(3)、求⊙O的半径.35. 如图,A,B,C是方格纸中的格点,请按要求作图.
(1)、用直尺和圆规作出△ABC的外接圆⊙O (不写作法,保留作图痕迹);(2)、求∠AOC的度数;(3)、求⊙O的半径.35. 如图,A,B,C是方格纸中的格点,请按要求作图. (1)、在图1中画出一个以A,B,C,D为顶点的格点平行四边形.(2)、在图2中画出一个格点P,使得∠BPC= ∠BAC.
(1)、在图1中画出一个以A,B,C,D为顶点的格点平行四边形.(2)、在图2中画出一个格点P,使得∠BPC= ∠BAC.九、圆中有关线段的计算
-
36. 已知四边形内接于 , 对角线是的直径.
 (1)、如图1,连接 , 若 , 求证;平分;(2)、如图2,为内一点,满足 , 若 , , 求弦的长.37. 如图,是的直径,点C、D、E在上,若 , , 且 , 则为( )
(1)、如图1,连接 , 若 , 求证;平分;(2)、如图2,为内一点,满足 , 若 , , 求弦的长.37. 如图,是的直径,点C、D、E在上,若 , , 且 , 则为( )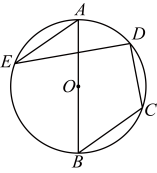 A、 B、6 C、 D、
A、 B、6 C、 D、