湖南省长沙市五校联考2023-2024学年八年级上学期月考数学试题
试卷更新日期:2024-01-25 类型:月考试卷
一、选择题(共10小题,每小题3分,共30分)
-
1. 随着自主研发能力的增强,我国在制造芯片最重要也是最艰难的技术上有了新突破——光刻机,将在2021~2022年交付第一台28nm工艺的国产沉浸式光刻机,其中数据28nm(即0.000000028m)用科学记数法可表示为( )A、 B、 C、 D、2. 要使分式有意义,则的取值应满足( )A、 B、 C、 D、3. 在下列运算中,计算正确的是( )A、 B、 C、 D、4. 一个等腰三角形的两边长分别为3cm,4cm,则它的周长是( )A、11cm B、10cm C、10cm或7cm D、11cm或10cm5. 下列各式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、6. 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是( )A、6 B、7 C、8 D、97. 若点 , 关于轴对称,则( )A、; B、; C、; D、;8. 若展开后不含的一次项,则的值是( )A、3 B、1 C、 D、09. 将分式中的 , 的值同时扩大到原来的2倍,则分式的值( )A、扩大到原来的2倍 B、保持不变 C、缩小到原来的 D、无法确定10. 如图,是的角平分线, , 垂足为 , 交的延长线于点 , 若恰好平分 , .给出下列四个结论:①;②;③;④ , 其中正确的结论共有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(共6小题,每小题3分,共18分)
-
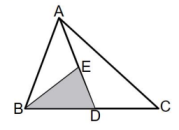
11. 计算:.12. 若分式的值为0,则.13. 若x2+mx+16是完全平方式,则m= .14. 如图所示,在中,点 , 分别为 , 的中点,且 , 则阴影部分的面积为.
 15. 已知 , , 则.16. 关于的分式方程无解,则.
15. 已知 , , 则.16. 关于的分式方程无解,则.三、解答题(共9小题,共72分)
-
17.(1)、计算:(2)、因式分解:(3)、化简:(4)、计算:18. 解分式方程:(1)、(2)、19. 先化简,再求值: ,其中 .20. 如图,的延长线于 , 于 , 若 , .
 (1)、求证:;(2)、求证:平分.21. 平面直角坐标系中,各顶点坐标分别为、、 .
(1)、求证:;(2)、求证:平分.21. 平面直角坐标系中,各顶点坐标分别为、、 . (1)、若与关于轴对称,请在平面直角坐标系中画;(2)、的面积是;(3)、已知为轴上一点,若的面积为4,求点的坐标.22. 为了迎接在杭州举行的第19届亚运会,某旅游商店购进若干吉祥物钥匙扣和明信片,已知吉祥物钥匙扣的进价为18元/个,明信片的进价为6元/套,一个吉祥物钥匙扣的售价比一套明信片的售价高20元.若顾客花150元购买的吉祥物钥匙扣数量与花50元购买的明信片数量相同.(1)、求吉祥物钥匙扣和明信片的售价;(2)、为了促销,商店对吉祥物钥匙扣进行9折销售,某顾客同时购买吉祥物钥匙扣和明信片两种商品若干件,商家获毛利80元,请问有几种购买方案.23. 如图
(1)、若与关于轴对称,请在平面直角坐标系中画;(2)、的面积是;(3)、已知为轴上一点,若的面积为4,求点的坐标.22. 为了迎接在杭州举行的第19届亚运会,某旅游商店购进若干吉祥物钥匙扣和明信片,已知吉祥物钥匙扣的进价为18元/个,明信片的进价为6元/套,一个吉祥物钥匙扣的售价比一套明信片的售价高20元.若顾客花150元购买的吉祥物钥匙扣数量与花50元购买的明信片数量相同.(1)、求吉祥物钥匙扣和明信片的售价;(2)、为了促销,商店对吉祥物钥匙扣进行9折销售,某顾客同时购买吉祥物钥匙扣和明信片两种商品若干件,商家获毛利80元,请问有几种购买方案.23. 如图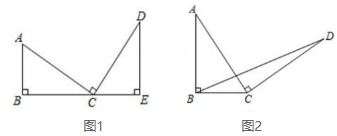 (1)、如图1,与中, , , 、、三点在同一直线上, , , 求的长.(2)、如图2,在中, , , 过点作 , 且 , 求的面积.24. 我们知道,任意一个正整数都可以进行这样的分解:( , 是正整数,且),在的所有这种分解中,如果 , 两因数之差的绝对值最小,我们就称是的最佳分解,并规定: . 例如:18可以分解成 , 或 , 因为 , 所以是18的最佳分解,所以 .(1)、;;(为正整数);(2)、若是正整数,①猜想的表达式;②若 , 求的值;(3)、若 , 其中是整数,求的值.25. 已知为等边三角形,取的边 , 中点 , , 连接 , 如图1,易证为等边三角形,将绕点顺时针旋转,设旋转的角度 , 其中.
(1)、如图1,与中, , , 、、三点在同一直线上, , , 求的长.(2)、如图2,在中, , , 过点作 , 且 , 求的面积.24. 我们知道,任意一个正整数都可以进行这样的分解:( , 是正整数,且),在的所有这种分解中,如果 , 两因数之差的绝对值最小,我们就称是的最佳分解,并规定: . 例如:18可以分解成 , 或 , 因为 , 所以是18的最佳分解,所以 .(1)、;;(为正整数);(2)、若是正整数,①猜想的表达式;②若 , 求的值;(3)、若 , 其中是整数,求的值.25. 已知为等边三角形,取的边 , 中点 , , 连接 , 如图1,易证为等边三角形,将绕点顺时针旋转,设旋转的角度 , 其中. (1)、如图2,当 , 连接 , , 求证:;(2)、在旋转过程中,当超过一定角度时,如图3,连接 , 会交于一点,记交点为点 , 交于点 , 交于点 , 连接 , 请问是否会平分?如果是,求出 , 如果不是,请说明理由;(3)、在第(2)问的条件下,试猜想线段 , 和之间的数量关系,并说明理由.
(1)、如图2,当 , 连接 , , 求证:;(2)、在旋转过程中,当超过一定角度时,如图3,连接 , 会交于一点,记交点为点 , 交于点 , 交于点 , 连接 , 请问是否会平分?如果是,求出 , 如果不是,请说明理由;(3)、在第(2)问的条件下,试猜想线段 , 和之间的数量关系,并说明理由.