吉林省松原市扶余市2023-2024学年九年级上学期数学期末考试试卷

试卷更新日期：2024-01-25 类型：期末考试

进入出卷网下载

一、单项选择题（每小题2分，共12分）

1. 有下列现象：①地下水位逐年下降：②传送带的移动；③方向盘的转动：④水龙头开关的转动；⑤钟摆的运动：⑥荡秋千运动。其中属于旋转的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 《九章算术》是我国古代著名数学著作，书中记载：“今有圆材，埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺，问径几何？”用数学语言可表述为：“如图，CD为⊙O的直径，弦AB⊥DC于E，ED=1寸，AB=10寸，求直径CD的长。”则CD为（）

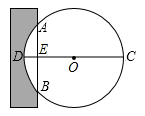A、10寸 B、3寸 C、20寸 D、26寸

查看试题解析
3. 在一个不透明的盒子里有2个红球和n个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个，摸到红球的概率是 $\frac{1}{5}$ ，则n的值为（）

A、3 B、8 C、5 D、10

查看试题解析
4. 若关于x的一元二次方程 $k x^{2} - 6 x + 9 = 0$ 有实数根，则k的取值范围是（）

A、 $k < 1$ B、 $k \leq 1$ C、 $k < 1$ 且 $k \neq 0$ D、 $k \leq 1$ 且 $k \neq 0$

查看试题解析
5. 将抛物线 $y = x^{2}$ 向上平移3个单位，所得抛物线的解析式是（　　）

A、 $y = x^{2} + 3$ B、 $y = x^{2} - 3$ C、 $y = {(x + 3)}^{2}$ D、 $y = {(x - 3)}^{2}$

查看试题解析
6. 已知近视眼镜的度数y（度）与镜片焦距x（米）之间成反比例函数关系，如图所示，则眼镜度数y与镜片焦距x之间的函数关系式是（　　）

A、 $y = 100 x$ B、 $y = 200 x$ C、 $y = \frac{100}{x}$ D、 $y = \frac{200}{x}$

查看试题解析

二、填空题（每小题3分，共24分）

7. 请填写一个常数，使得关于 $x$ 的方程 $x^{2} - 2 x +$ $= 0$ 有两个不相等的实数根.

查看试题解析
8. 有甲、乙两把不同的锁和A、B、C三把不同的钥匙．其中两把钥匙分别能打开这两把锁，第三把钥匙不能打开这两把锁．随机取出一把钥匙开甲锁，恰好能打开的概率是．

查看试题解析
9. 若方程 $(m - 1) x^{2} - 4 x + 3 = 0$ 是一元二次方程，当m满足条件．

查看试题解析
10. 近年来我市大力发展旅游产业，已知旅游总收入从2015年的150亿元上升到2017年的216亿元，设这两年旅游总收入的年平均增长率为x ，则可列方程．

查看试题解析
11. 如图，函数y= $\frac{k}{x}$ （x>0）的图象过矩形OBCD一边的中点，且图象过矩形OAPE的顶点P，若阴影部分面积为6，则k的值为

查看试题解析
12. 如图，点A、B、C在⊙O上，∠B=130°，则∠AOC=°．

查看试题解析
13. 如图，图中网格由边长为1的小正方形组成，点 $A$ 为网格线的交点.若线段 $O A$ 绕原点 $O$ 顺时针旋转90°后，端点 $A$ 的坐标变为.

查看试题解析
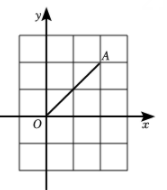14. 如图，抛物线y=ax²﹣4和y=﹣ax²+4都经过x轴上的A、B两点，两条抛物线的顶点分别为C、D．当四边形ACBD的面积为40时，a的值为．

查看试题解析

三、解答题（每小题5分，共20分）

15. 解方程： $2 x^{2} + 6 x + 3 = 0$ ．

查看试题解析
16. 已知抛物线 $y = a x^{2} + b x + c$ 的顶点坐标为（－1，4），与 $x$ 轴两交点间的距离为6，求此抛物线的函数关系式．

查看试题解析
17. 如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径，∠BAC=25°．求∠P的度数．

查看试题解析
18. 如图所示，正方形网格中， $△ A B C$ 为格点三角形（即三角形的顶点都在格点上）．

(1)、把 $△ A B C$ 沿 $B A$ 方向平移后，点 $A$ 移到点 $A_{1}$ ，在网格中画出平移后得到的 $△ A_{1} B_{1} C_{1}$ ；

(2)、把 $△ A_{1} B_{1} C_{1}$ 绕点 $A_{1}$ 按逆时针方向旋转 $90 °$ ，在网格中画出旋转后的 $△ A_{1} B_{2} C_{2}$ ．

查看试题解析

四、解答题（每小题7分，共28分）

19. 为进一步深化基础教育课程改革，构建符合素质教育要求的学校课程体系，某学校自主开发了A书法，B阅读，C足球，D器乐四门校本选修课程供学生选择．每门课程被选到的机会均等．

(1)、学生小红计划选修两门课程，所有可能的选法有种．

(2)、若学生小明和小刚各计划选修一门课程，则他们两人恰好选修同一门课程的概率为多少？

查看试题解析
20. 已知：如图， $△$ ABC为锐角三角形，AB=AC，CD∥AB．
求作：线段BP，使得点P在直线CD上，且∠ABP= $\frac{1}{2} ∠ B A C$ ．
作法：①以点A为圆心，AC长为半径画圆，交直线CD于C，P两点；②连接BP．线段BP就是所求作线段．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）

(2)、完成下面的证明．
证明：∵CD∥AB，
∴∠ABP= ▲ ．
∵AB=AC，
∴点B在⊙A上．
又∵∠BPC= $\frac{1}{2}$ ∠BAC（）（填推理依据）
∴∠ABP= $\frac{1}{2}$ ∠BAC

查看试题解析
21. 已知关于x的一元二次方程x²+2x﹣（m﹣2）＝0有实数根．

(1)、求m的取值范围；

(2)、若方程有一个根为x＝1，求m的值及另一个根．

查看试题解析
22. 百货大楼服装柜在销售中发现：“宝乐”牌童装平均每天可售出20件，每件盈利40元．为了迎接“十·一”国庆节，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存，经市场调查发现：如果每件童装降价1元，那么平均每天就可多售出2件，要想平均每天销售这种童装上盈利1200元，那么每件童装应降价多少元？

查看试题解析

五、解答题（每小题8分，共16分）

23. 为了预防疾病，某单位对办公室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成为正比例，药物燃烧后，y与x成反比例（如图），现测得药物8分钟燃毕，此时室内空气中每立方米的含药量6毫克，请根据题中所提供的信息，解答下列问题：

(1)、药物燃烧时，y关于x的函数关系式为，自变量x的取值范围为；药物燃烧后，y关于x的函数关系式为 .

(2)、研究表明，当空气中每立方米的含药量低于1.6毫克时员工方可进办公室，那么从消毒开始，至少需要经过分钟后，员工才能回到办公室；

(3)、研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？

查看试题解析
24. 自主学习，请阅读下列解题过程．
解一元二次不等式： $x^{2} - 5 x$ ＞0．
解：设 $x^{2} - 5 x$ =0，解得： $x_{1}$ =0， $x_{2}$ =5，则抛物线y= $x^{2} - 5 x$ 与x轴的交点坐标为（0，0）和（5，0）．画出二次函数y= $x^{2} - 5 x$ 的大致图象（如图所示），由图象可知：当x＜0，或x＞5时函数图象位于x轴上方，此时y＞0，即 $x^{2} - 5 x$ ＞0，所以，一元二次不等式 $x^{2} - 5 x$ ＞0的解集为：x＜0或x＞5．
通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：

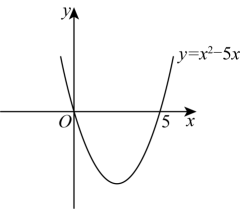(1)、上述解题过程中，渗透了下列数学思想中的和．（只填序号）
①转化思想 ②分类讨论思想 ③数形结合思想

(2)、一元二次不等式 $x^{2} - 5 x$ ＜0的解集为．

(3)、用类似的方法解一元二次不等式： $x^{2} - 2 x - 3$ ＞0．

查看试题解析

六、解答题（每小题10分，共20分）

25. 定义：对多边形进行折叠，若翻折后的图形恰能拼成一个无缝隙、无重叠的四边形，则这样的四边形称为镶嵌四边形．

(1)、如图1，将 $△ A B C$ 纸片沿中位线 $E H$ 折叠，使点 $A$ 落在 $B C$ 边上的 $D$ 处，再将纸片分别沿 $E F$ ， $H G$ 折叠，使点 $B$ 和点 $C$ 都与点 $D$ 重合，得到双层四边形 $E F G H$ ，则双层四边形 $E F G H$ 为形．

(2)、 $▱ A B C D$ 纸片按图2的方式折叠，折成双层四边形 $E F G H$ 为矩形，若 $E F = 5$ ， $E H = 12$ ，求 $A D$ 的长．

(3)、如图3，四边形 $A B C D$ 纸片满足 $A D ∥ B C$ ， $A D < B C$ ， $A B ⊥ B C$ ， $A B = 8$ ， $C D = 10$ ．把该纸片折叠，得到双层四边形为正方形．请你画出一种折叠的示意图，并直接写出此时 $B C$ 的长．

查看试题解析
26. 如图，已知抛物线y=ax²+bx+c（a≠0）经过A（3，0），B（﹣5，0），C（0，﹣5）三点，O为坐标原点.

(1)、求此抛物线的解析式；

(2)、把抛物线y=ax²+bx+c（a≠0）向上平移 $\frac{13}{3}$ 个单位长度，再向左平移n（n＞0）个单位长度得到新抛物线，若新抛物线的顶点M在△ABC内，求n的取值范围；

(3)、设点P在y轴上，且满足∠OPA+∠OCA=∠CBA，求CP的长.

查看试题解析