北京市昌平区2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-01-25 类型:期末考试
一、选择题(共8道小题,每小题2分,共16分)第1-8题均有四个选项,符合题意的选项只有一个
-
1. 如图,这是一张海上日出照片,如果把太阳看作一个圆,把海平面看作一条直线,那么这个圆与这条直线的位置关系是( )
 A、相离 B、相切 C、相交 D、不确定2. 如果 , 那么下列比例式成立的是( )A、 B、 C、 D、3. 将抛物线向左平移2个单位长度,再向下平移3个单位长度,所得到的抛物线的表达式为( )A、 B、 C、 D、4. 如图,点A , B , C , D在⊙O上,AC是⊙O的直径,∠BAC=40°,则∠D的度数是( )
A、相离 B、相切 C、相交 D、不确定2. 如果 , 那么下列比例式成立的是( )A、 B、 C、 D、3. 将抛物线向左平移2个单位长度,再向下平移3个单位长度,所得到的抛物线的表达式为( )A、 B、 C、 D、4. 如图,点A , B , C , D在⊙O上,AC是⊙O的直径,∠BAC=40°,则∠D的度数是( ) A、40° B、50° C、60° D、90°5. 在平面直角坐标系xOy中,若点和在反比例函数图象上,则下列关系式正确的是( )A、 B、 C、 D、6. 如图,一艘轮船航行至O点时,测得某灯塔A位于它的北偏东40°方向,且它与灯塔A相距13海里,继续沿正东方向航行,航行至点B处时,测得灯塔A恰好在它的正北方向,则的距离可表示为( )
A、40° B、50° C、60° D、90°5. 在平面直角坐标系xOy中,若点和在反比例函数图象上,则下列关系式正确的是( )A、 B、 C、 D、6. 如图,一艘轮船航行至O点时,测得某灯塔A位于它的北偏东40°方向,且它与灯塔A相距13海里,继续沿正东方向航行,航行至点B处时,测得灯塔A恰好在它的正北方向,则的距离可表示为( )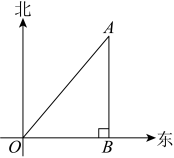 A、海里 B、海里 C、海里 D、海里7. 如图,在等腰中,于点 , 则的值( )
A、海里 B、海里 C、海里 D、海里7. 如图,在等腰中,于点 , 则的值( )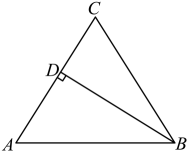 A、 B、 C、 D、8. 如图,是等边三角形,D , E分别是 , 边上的点,且 , 连接 , 相交于点F , 则下列说法正确的是( )
A、 B、 C、 D、8. 如图,是等边三角形,D , E分别是 , 边上的点,且 , 连接 , 相交于点F , 则下列说法正确的是( )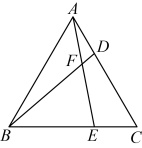
①; ②;③;④若 , 则
A、①②③ B、①②④ C、②③④ D、①③④二、填空题(共8道小题,每小题2分,共16分)
-
9. 写出一个开口向下且过的抛物线的表达式 .10. 如图,M为反比例函数的图象上的一点 , 轴,垂足为A , 的面积为3,则k的值为 .
 11. 在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同,天下一家”的主题,让世界观众感受了中国人的浪漫.如图,作出“雪花”图案(正六边形)的外接圆,已知正六边形的边长是4,则长为 .
11. 在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同,天下一家”的主题,让世界观众感受了中国人的浪漫.如图,作出“雪花”图案(正六边形)的外接圆,已知正六边形的边长是4,则长为 .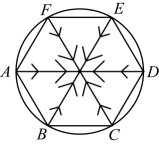 12. 如图,在平行四边形中,E为的中点, , 交于点F , 则和的面积比为 .
12. 如图,在平行四边形中,E为的中点, , 交于点F , 则和的面积比为 . 13. 如图,在中,半径垂直弦于点D , 若 , , 则的长为 .
13. 如图,在中,半径垂直弦于点D , 若 , , 则的长为 .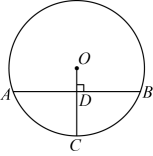 14. 小明同学测量一个圆形零件的半径时,他将直尺、三角板和这个零件如图放置于桌面上,零件与直尺,三角板均相切,测得点A与其中一个切点B的距离为3cm,则这个零件的半径是cm.
14. 小明同学测量一个圆形零件的半径时,他将直尺、三角板和这个零件如图放置于桌面上,零件与直尺,三角板均相切,测得点A与其中一个切点B的距离为3cm,则这个零件的半径是cm.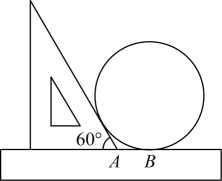 15. 如图,是直径,点C是上一点,且 , 点D是的中点,点P是直径上一动点,则的最小值为 .
15. 如图,是直径,点C是上一点,且 , 点D是的中点,点P是直径上一动点,则的最小值为 .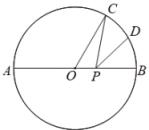 16. 已知抛物线(a , b , c为常数,)的对称轴是直线 , 其部分图象如图,则以下四个结论中:①;②;③;④ . 其中,正确结论的序号是 .
16. 已知抛物线(a , b , c为常数,)的对称轴是直线 , 其部分图象如图,则以下四个结论中:①;②;③;④ . 其中,正确结论的序号是 .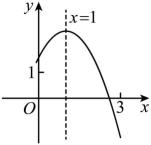
三、解答题(本题共12道小题,第17题5分,第18题4分,第19题6分,第20-22题,每小题5分,第23-26题,每小题6分,第27、28题,每小题7分,共68分)
-
17. 计算: .18. 如图,中,点D是边AB上一点,点E为外一点, , 连接BE . 从下列条件中:①;② . 选择一个作为添加的条件,求证: .
 19. 已知二次函数的y与x的部分对应值如下表:
19. 已知二次函数的y与x的部分对应值如下表:x
…
1
3
…
y
…
0
1
0
…
 (1)、求这个二次函数表达式;(2)、在平面直角坐标系中画出这个函数图象;(3)、当x的取值范围为时, .20. 如图,在中, , 于点D , , , 求及的长.
(1)、求这个二次函数表达式;(2)、在平面直角坐标系中画出这个函数图象;(3)、当x的取值范围为时, .20. 如图,在中, , 于点D , , , 求及的长. 21. 已知:如图,在中, .
21. 已知:如图,在中, .求作:射线 , 使得 .
作法:①以点A为圆心,长为半径画圆;
②延长交于点D , 以点D为圆心,长为半径画弧,与交于点P(点C , P在线段的同侧);
③作射线 .
射线即为所求.
 (1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明证明:连接 .
∵ ,
∴点C在上.
∵ ,
∴()(填推理依据).
∵ ,
∴ .
∴ .
22. 如图,在平面直角坐标系中,点在双曲线上,点B在双曲线上,且满足 , 连接 . (1)、求双曲线的表达式;(2)、若 , 求的值.23. 某校组织九年级学生参加社会实践活动,数学学科的项目任务是测量银山塔林中某塔的高度 , 其中一个数学兴趣小组设计的方案如图所示,他们在点C处用高1.5m的测角仪测得塔顶A的仰角为 , 然后沿方向前行7m到达点F处,在F处测得塔顶A的仰角为 . 请根据他们的测量数据求塔高的长度大约是多少.(参考数据: , , , , , . )
(1)、求双曲线的表达式;(2)、若 , 求的值.23. 某校组织九年级学生参加社会实践活动,数学学科的项目任务是测量银山塔林中某塔的高度 , 其中一个数学兴趣小组设计的方案如图所示,他们在点C处用高1.5m的测角仪测得塔顶A的仰角为 , 然后沿方向前行7m到达点F处,在F处测得塔顶A的仰角为 . 请根据他们的测量数据求塔高的长度大约是多少.(参考数据: , , , , , . )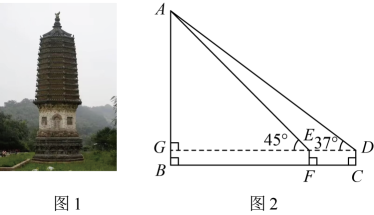 24. 如图,是的直径,点在上,点为的中点,过点作的切线,交延长线于点 , 连接交于点 .
24. 如图,是的直径,点在上,点为的中点,过点作的切线,交延长线于点 , 连接交于点 .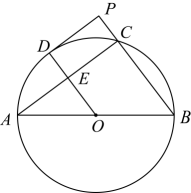 (1)、求证:四边形是矩形;(2)、作射线交的延长线于点F , 若 , , 求的长.25. 如图,小静和小林在玩沙包游戏,沙包(看成点)抛出后,在空中的运动轨迹可看作抛物线的一部分,小静和小林分别站在点O和点A处,测得距离为 , 若以点O为原点,所在直线为x轴,建立如图所示的平面直角坐标系,小林在距离地面的B处将沙包抛出,其运动轨迹为抛物线:的一部分,小静恰在点处接住,然后跳起将沙包回传,其运动轨迹为抛物线:的一部分.
(1)、求证:四边形是矩形;(2)、作射线交的延长线于点F , 若 , , 求的长.25. 如图,小静和小林在玩沙包游戏,沙包(看成点)抛出后,在空中的运动轨迹可看作抛物线的一部分,小静和小林分别站在点O和点A处,测得距离为 , 若以点O为原点,所在直线为x轴,建立如图所示的平面直角坐标系,小林在距离地面的B处将沙包抛出,其运动轨迹为抛物线:的一部分,小静恰在点处接住,然后跳起将沙包回传,其运动轨迹为抛物线:的一部分.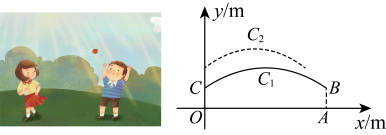 (1)、抛物线的最高点坐标为;(2)、求a , c的值;(3)、小林在x轴上方的高度上,且到点A水平距离不超过的范围内可以接到沙包,若小林成功接到小静的回传沙包,则n的整数值可为 .26. 在平面直角坐标系中,点 , 在抛物线上.(1)、当时,求抛物线的对称轴;(2)、若抛物线经过点 , 当自变量x的值满足时,y随x的增大而增大,求a的取值范围;(3)、当时,点 , 在抛物线上.若 , 请直接写出m的取值范围.27. 在中, , , 点M为的中点,连接 , 点D为线段上一动点,过点D作 , 且 , (点E在的上方),连接 , 过点E作的垂线交边于点F .
(1)、抛物线的最高点坐标为;(2)、求a , c的值;(3)、小林在x轴上方的高度上,且到点A水平距离不超过的范围内可以接到沙包,若小林成功接到小静的回传沙包,则n的整数值可为 .26. 在平面直角坐标系中,点 , 在抛物线上.(1)、当时,求抛物线的对称轴;(2)、若抛物线经过点 , 当自变量x的值满足时,y随x的增大而增大,求a的取值范围;(3)、当时,点 , 在抛物线上.若 , 请直接写出m的取值范围.27. 在中, , , 点M为的中点,连接 , 点D为线段上一动点,过点D作 , 且 , (点E在的上方),连接 , 过点E作的垂线交边于点F .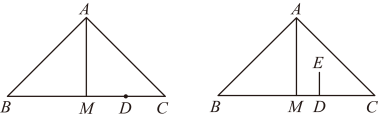 (1)、如图1,当点D为的中点时,
(1)、如图1,当点D为的中点时,①依题意补全图形;
②直接写出和的数量关系为 ▲ ;
(2)、当点D在图2的位置时,用等式表示线段和之间的数量关系,并证明.28. 对于在平面直角坐标系中和外的点P , 给出如下定义:已知的半径为1,若上存在点Q , 满足 , 则称点P为的关联点.(1)、如图,若点T的坐标为 ,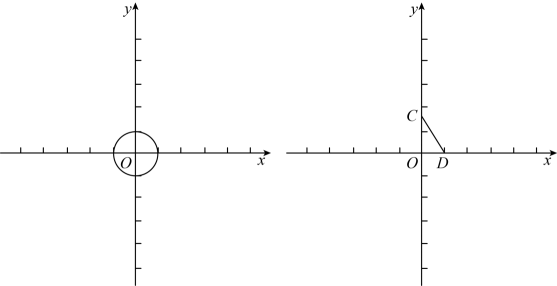
①在点 , , 中,是的关联点的是 ▲ ;
②直线分别交x轴,y轴于点A , B , 若线段AB存在的关联点,求b的取值范围;
(2)、已知点 , , , 上的每一个点都是的关联点,直接写出m的取值范围.