北京市大兴区2023-2024学年八年级上学期期末数学试卷
试卷更新日期:2024-01-25 类型:期末考试
一、选择题:本题共8小题,每小题2分,共16分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 将用科学记数法表示应为( )A、 B、 C、 D、2. 下列运算中正确的是( )A、 B、 C、 D、3. 下列各式中,能用平方差公式进行因式分解的是( )A、 B、 C、 D、4. 若分式的值为0,则x的值为( )A、1 B、-1 C、0 D、±15. 已知是完全平方式,则的值为( )A、 B、 C、 D、6. 在平面直角坐标系中,点关于轴对称的点的坐标是( )A、 B、 C、 D、7. 已知等腰三角形的一边长为4,另一边长为8,则它的周长是( ).A、 B、 C、 D、 或8. 如图,某小区规划在边长为的正方形场地上,修建两条宽为的甬道,其余部分种草,则甬道所占的面积单位是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共8小题,每小题2分,共16分。
-
9. 若分式有意义,则的取值范围是 .10. 计算: .11. 计算: .12. 分解因式:3x2-6x+3= .13. 如图,是等边三角形, , 平分交于点 , 则线段的长为 .
 14. 如图, , , 要使≌ , 则需再添加一个条件是写出一个即可 .
14. 如图, , , 要使≌ , 则需再添加一个条件是写出一个即可 . 15. 如图是两个全等三角形,图中的字母表示三角形的边长,那么的度数为 .
15. 如图是两个全等三角形,图中的字母表示三角形的边长,那么的度数为 . 16. 如图,的角平分线 , 相交于点 , , , 且于点 , 下列结论:;平分;; , 其中正确的结论是只填序号 .
16. 如图,的角平分线 , 相交于点 , , , 且于点 , 下列结论:;平分;; , 其中正确的结论是只填序号 .
三、计算题:本大题共1小题,共5分。
-
17. 先化简,再求值:(x+y)(x-y)-x(x-2y),其中x= , y=3.
四、解答题:本题共11小题,共63分。解答应写出文字说明,证明过程或演算步骤。
-
18. 计算: .19. 计算: .20. 计算: .21. 已知:如图,点 , , , 顺次在同一条直线上,点 , 在直线的同侧, , , 求证: .
 22. 解方程: .23. 求证:当是整数时,两个连续奇数的平方差是这两个奇数的和的倍.24. 小月是学校图书馆书库的志愿者,小杰是学校图书馆书库的志愿者,他们各自负责本书库的整理工作月日,图书馆书库有册图书需整理,而书库有册图书需整理,小月每小时整理图书的数量是小杰每小时整理图书数量的倍,他们同时开始工作,结果小杰比小月提前分钟完成工作求小月和小杰每小时分别可以整理多少册图书.25. 已知:如图,是等边三角形,点在边上,点关于直线的对称点为 , 连接 , 点是线段上的一点,连接 , , 延长到点 , 使 , 连接求证: .
22. 解方程: .23. 求证:当是整数时,两个连续奇数的平方差是这两个奇数的和的倍.24. 小月是学校图书馆书库的志愿者,小杰是学校图书馆书库的志愿者,他们各自负责本书库的整理工作月日,图书馆书库有册图书需整理,而书库有册图书需整理,小月每小时整理图书的数量是小杰每小时整理图书数量的倍,他们同时开始工作,结果小杰比小月提前分钟完成工作求小月和小杰每小时分别可以整理多少册图书.25. 已知:如图,是等边三角形,点在边上,点关于直线的对称点为 , 连接 , 点是线段上的一点,连接 , , 延长到点 , 使 , 连接求证: .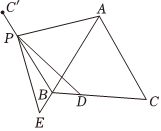 26. 已知:如图,在中, , 设 , , 如果 .
26. 已知:如图,在中, , 设 , , 如果 . (1)、求证:是等边三角形;(2)、的中线 , 交于点 , 用等式表示线段与之间的数量关系,并证明.27. 已知:如图, , , , 连接 , , , 过点作于点 , 过点作的高线 , 交的延长线于点 .
(1)、求证:是等边三角形;(2)、的中线 , 交于点 , 用等式表示线段与之间的数量关系,并证明.27. 已知:如图, , , , 连接 , , , 过点作于点 , 过点作的高线 , 交的延长线于点 . (1)、求证:≌;(2)、求的度数.28. 在平面直角坐标系中,对于 , 两点给出如下定义:若点的横纵坐标的绝对值之和等于点的横纵坐标的绝对值之和,则称 , 两点为“等和点”下图中的 , 两点即为“等和点”.
(1)、求证:≌;(2)、求的度数.28. 在平面直角坐标系中,对于 , 两点给出如下定义:若点的横纵坐标的绝对值之和等于点的横纵坐标的绝对值之和,则称 , 两点为“等和点”下图中的 , 两点即为“等和点”.
 (1)、已知点的坐标为 ,
(1)、已知点的坐标为 ,在点 , , 中,与点为“等和点”的是只填字母;
若点在第一象限的角平分线上,且 , 两点为“等和点”,则点的坐标为 ;
(2)、已知点的坐标为 , 点的坐标为 , 连接 , 点为线段上一点,过点作轴的垂线 , 若垂线上存在点的“等和点”,求的取值范围.
-