吉林省松原市2022-2023学年八年级下学期数学月考考试试卷(3月)
试卷更新日期:2024-01-25 类型:月考试卷
一、选择题(每小题2分,共12分)
-
1. 下列式子是二次根式的是( )A、 B、 C、 D、2. 若 , 则“□”内的运算符号为( )A、 B、 C、 D、3. 下列二次根式,化简后能与合并的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,两个较大的正方形的面积分别为225和289,则字母所代表的正方形的面积为( )
 A、64 B、16 C、8 D、46. 如图,在中,已知 . 以为直角边,构造;再以为直角边,构造;…,按照这个规律,在中,点到的距离是( )
A、64 B、16 C、8 D、46. 如图,在中,已知 . 以为直角边,构造;再以为直角边,构造;…,按照这个规律,在中,点到的距离是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共24分)
-
7. 若二次根式 在实数范围内有意义,则 的取值范围是.8. 计算: .9. 计算:+= .
10. 若与最简二次根式可以合并,则 .11. 如图,任中, , 茷 , 则的长为 . 12. 如图,在中, , 以点为圆心,以长为半径画弧,交于点 . 若 , , 则的周长为 .
12. 如图,在中, , 以点为圆心,以长为半径画弧,交于点 . 若 , , 则的周长为 . 13. 如图,在平面直角坐标系中,已知 , 点分别在第一、二象限,且轴.若 , 点的横坐标为2,则点的坐标是 .
13. 如图,在平面直角坐标系中,已知 , 点分别在第一、二象限,且轴.若 , 点的横坐标为2,则点的坐标是 . 14. 如图,在中, , 将沿翻折,使点与点重合若 , , 则的长为 .
14. 如图,在中, , 将沿翻折,使点与点重合若 , , 则的长为 .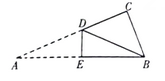
三、解答题(每小题5分,共20分)
-
15. 计算: .16. 计算: .17. 计算: .18. 如图是的正方形网格,每个小正方形的顶点称为格点,小正方形的边长均为1,点A在格点上.用无刻度的直尺在图中以点A为一个顶点画一个面积为5的等腰直角三角形 , 要求点B , C在格点上.

四、解答题(每小题7分,共28分)
-
19. 若 , 求的值.20. 求图中四边形的面积.
 21. 如图,有人站在离水面高度为8米的岸上A处,用绳子拉船靠岸,开始时绳子的长为17米,此人以1米/秒的速度收绳,7秒后船移动到点C的位置,求此时船向岸边移动的距离是多少米(假设绳子是直的)?
21. 如图,有人站在离水面高度为8米的岸上A处,用绳子拉船靠岸,开始时绳子的长为17米,此人以1米/秒的速度收绳,7秒后船移动到点C的位置,求此时船向岸边移动的距离是多少米(假设绳子是直的)? 22. 如图①,在的正方形网格中,每个小正方形的边长均为1.
22. 如图①,在的正方形网格中,每个小正方形的边长均为1. (1)、图①中正方形的面积为;边长为;(2)、如图②,若点在数轴上表示的数是 , 以为圆心,长为半径画圆弧,与数轴的正半轴交于点 , 求点表示的数.
(1)、图①中正方形的面积为;边长为;(2)、如图②,若点在数轴上表示的数是 , 以为圆心,长为半径画圆弧,与数轴的正半轴交于点 , 求点表示的数.五、解答题(每小题8分,共16分)
-
23. 如图, , , , 一机器人在点B处看见一个小球从点A出发沿着方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球. 如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程是多少?
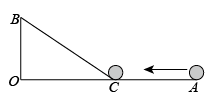 24. 如图,在中,于点 .
24. 如图,在中,于点 . (1)、求的长;(2)、求的长.
(1)、求的长;(2)、求的长.六、解答题(每小题10分,共20分)
-
25. 数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观,从而可以帮助我们快速解题,初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
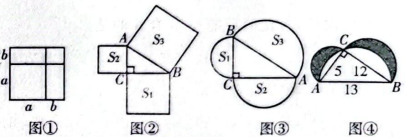 (1)、如图①,是一个重要公式的几何解释,请你写出这个公式;(2)、如图②,在中, , 以的三边为边长向外作正方形,面积分别为 , 试猜想之间存在的等量关系,直接写出结论;(3)、如图③,如果以的三边长为直径向外作半圆,那么(2)问的结论是否成立?请说明理由;(4)、如图④,在中, , 三边长分别为5,12,13,分别以它的三边为直径向上作半圆,则图④中阴影部分的面积和为 .26. 如图,在中, , 点从点出发,以每秒2个单位长度的速度沿向终点运动.设点运动的时间为秒 .
(1)、如图①,是一个重要公式的几何解释,请你写出这个公式;(2)、如图②,在中, , 以的三边为边长向外作正方形,面积分别为 , 试猜想之间存在的等量关系,直接写出结论;(3)、如图③,如果以的三边长为直径向外作半圆,那么(2)问的结论是否成立?请说明理由;(4)、如图④,在中, , 三边长分别为5,12,13,分别以它的三边为直径向上作半圆,则图④中阴影部分的面积和为 .26. 如图,在中, , 点从点出发,以每秒2个单位长度的速度沿向终点运动.设点运动的时间为秒 .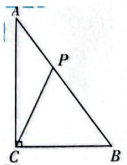 (1)、求的长;(2)、用含的代数式表示的长;(3)、当是直角三角形时,求的值;(4)、直接写出是等腰三角形时的值.
(1)、求的长;(2)、用含的代数式表示的长;(3)、当是直角三角形时,求的值;(4)、直接写出是等腰三角形时的值.