北京市大兴区2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-01-25 类型:期末考试
一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个.
-
1. 大兴国际机场航站楼是全球唯一一座“双进双出”的航站楼,也是世界施工技术难度最高的航站楼,航站楼一共使用了块玻璃,白天室内几乎不需要照明灯光.将 用科学记数法表示为( )A、 B、 C、 D、2. 的绝对值是( )A、5 B、 C、 D、±53. 如图,是由下列哪个立体图形展开得到的( )
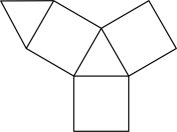 A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱4. 下列各对数中,互为相反数的是( )A、-(+3)与+(-3) B、-(-4)与|-4| C、-32与(-3)2 D、-23与(-2)35. 下列变形正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 如图,点是线段上一点, , 点是的中点,则的长为( )
A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱4. 下列各对数中,互为相反数的是( )A、-(+3)与+(-3) B、-(-4)与|-4| C、-32与(-3)2 D、-23与(-2)35. 下列变形正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 如图,点是线段上一点, , 点是的中点,则的长为( ) A、3 B、9 C、12 D、157. 如图,数轴上的点表示的数分别是 . 如果 , 且 , 那么该数轴的原点的位置应该在( )
A、3 B、9 C、12 D、157. 如图,数轴上的点表示的数分别是 . 如果 , 且 , 那么该数轴的原点的位置应该在( ) A、点的左侧 B、点的右侧 C、点与点之间且靠近点 D、点与点之间且靠近点8. 如图,点在一条直线上, , 那么的度数为( )
A、点的左侧 B、点的右侧 C、点与点之间且靠近点 D、点与点之间且靠近点8. 如图,点在一条直线上, , 那么的度数为( )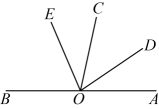 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共16分,每小题2分)
-
9. .10. 圆周率是数学美的象征,它的无限不循环小数形式引发了人们对数学的好奇和探索.圆周率 , 用四舍五入法把精确到百分位,得到的近似值是 .11. 若是关于的方程的解,则 .12. 写出一个含字母的一次二项式 , 满足当时,它的值等于5,这个式子可以是 .13. 计算: .14. 如图,某海域有三个小岛 , 在小岛O处观测到小岛A在它北偏东的方向上,观测到小岛B在它南偏东的方向上,则的度数是 .
 15. 一个角的补角等于这个角的2倍,则这个角的度数是 .16. 某学校把密码按照如下规律设置,根据提供的信息可以推断该校的密码是 .
15. 一个角的补角等于这个角的2倍,则这个角的度数是 .16. 某学校把密码按照如下规律设置,根据提供的信息可以推断该校的密码是 .账号:
密码
三、解答题(本题共68分,第17-21题,每题5分,第22题6分,第23题5分,第24-26题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.
-
17. 计算: .18.19. 计算: .20. 解方程: .21. 解方程: .22. 如图,已知平面内有四个点A , B , C , D . 根据下列语句按要求画图.
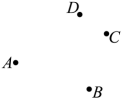 (1)、连接AB;(2)、作射线AD , 并在线段AD的延长线上用圆规截取DE=AB;(3)、作直线BC与射线AD交于点F . 观察图形发现,线段AF+BF>AB , 得出这个结论的依据是: ▲ .23. 先化简,再求值:
(1)、连接AB;(2)、作射线AD , 并在线段AD的延长线上用圆规截取DE=AB;(3)、作直线BC与射线AD交于点F . 观察图形发现,线段AF+BF>AB , 得出这个结论的依据是: ▲ .23. 先化简,再求值:,其中 .
24. 已知关于的方程 .(1)、当时,求方程的解;(2)、若 , 方程的解是整数,则有最(填“大”或“小”)值,这个值是 , 此时, .25. 如图,在数轴上有A , B , C , D四点,点A表示的数是1,点B表示的数是7,点C位于点B的左侧并与点B的距离是2,点D是线段的中点.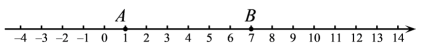 (1)、在数轴上表示出点C , 点D , 直接写出点D表示的数;(2)、若点E在数轴上,且满足 , 求点E表示的数.26. 某校组织若干师生到故宫进行参观活动,若学校只租用 45 座的客车,则刚好坐满;若只租用60座的客车,则可少租用1辆,且有一辆上只坐了15人,其余车辆都坐满.(1)、参加此次活动的师生共有多少人?
(1)、在数轴上表示出点C , 点D , 直接写出点D表示的数;(2)、若点E在数轴上,且满足 , 求点E表示的数.26. 某校组织若干师生到故宫进行参观活动,若学校只租用 45 座的客车,则刚好坐满;若只租用60座的客车,则可少租用1辆,且有一辆上只坐了15人,其余车辆都坐满.(1)、参加此次活动的师生共有多少人?下面是解决该问题的两种方法,请选择其中的一种方法完成分析和解答.
方法一
分析:设该校租用45座的客车需要x辆,则参观总人数可表示为 ▲ , 租用60座的客车(x-1)辆,则参观总人数可表示为 ▲ , 根据题意列方程.
方法二
分析:设该校参加此次活动的师生共有x人,则租用45座的客车需要 ▲ 辆,租用60座的客车需要 ▲ 辆,根据题意列方程.
(2)、若45座的客车每辆租金是1200元,60座的客车每辆租金是1500元,如果两种客车可以混租,请直接写出45座客车和60座客车各租多少辆时,费用最少.27. 如图, , 射线在内, .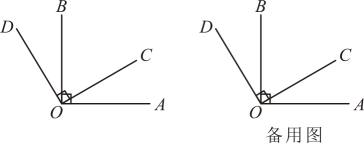 (1)、当时,请用量角器在图1中画出射线 , 求的度数;(2)、当时,平分 , 直接写出的度数.28. 点A , B , C在数轴上,对于线段和线段外一点C给出如下定义:若点C与线段上的点的最小距离小于或等于 , 则称点C是线段的 “半关联点”.(1)、如图,点A表示的数是1,点B表示的数是2,点D , E , F在数轴上,它们表示的数分别是 , 3,5,则在点D , E , F中,线段的 “半关联点”是;
(1)、当时,请用量角器在图1中画出射线 , 求的度数;(2)、当时,平分 , 直接写出的度数.28. 点A , B , C在数轴上,对于线段和线段外一点C给出如下定义:若点C与线段上的点的最小距离小于或等于 , 则称点C是线段的 “半关联点”.(1)、如图,点A表示的数是1,点B表示的数是2,点D , E , F在数轴上,它们表示的数分别是 , 3,5,则在点D , E , F中,线段的 “半关联点”是;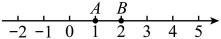 (2)、若点A表示的数是1,点B表示的数是2,且点C是线段的 “半关联点”,则点C表示的数c的取值范围是;(3)、若点A表示的数是1,如点C表示的数是 , 点C是线段的 “半关联点”,点B表示的数b的取值范围是 .
(2)、若点A表示的数是1,点B表示的数是2,且点C是线段的 “半关联点”,则点C表示的数c的取值范围是;(3)、若点A表示的数是1,如点C表示的数是 , 点C是线段的 “半关联点”,点B表示的数b的取值范围是 .