湖南省衡阳市南岳重点中学2023-2024学年九年级上学期期末数学试卷
试卷更新日期:2024-01-25 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 要使二次根式有意义,字母x必须满足的条件是( )A、x≥1 B、x>-1 C、x≥-1 D、x>12. 抛物线y=3x2向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )A、y=3(x-1)2-2 B、y=3(x+1)2-2 C、y=3(x+1)2+2 D、y=3(x-1)2+23. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
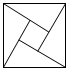 B、
B、 C、
C、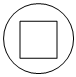 D、
D、 4. 关于的一元二次方程的一个根是 , 则的值是( )A、或 B、 C、 D、5. 若反比例函数的图象经过点 , 则的值为( )A、 B、 C、 D、6. 已知扇形的圆心角为 , 半径为 , 则弧长为( )A、 B、 C、 D、7. 如图,△AOB中,∠AOB=90°,现在将△AOB绕点O逆时针旋转44°,得到△A'OB',则∠A'OB的度数为( )
4. 关于的一元二次方程的一个根是 , 则的值是( )A、或 B、 C、 D、5. 若反比例函数的图象经过点 , 则的值为( )A、 B、 C、 D、6. 已知扇形的圆心角为 , 半径为 , 则弧长为( )A、 B、 C、 D、7. 如图,△AOB中,∠AOB=90°,现在将△AOB绕点O逆时针旋转44°,得到△A'OB',则∠A'OB的度数为( ) A、44° B、66° C、56° D、46°8. 七年级一班同学组织了元旦联欢会,文艺委员准备在“横扫千军”“飞花令”“成语接龙”“看图猜诗词”四个项目中选择两个,则她选中“飞花令”和“看图猜诗词”的概率为( )A、 B、 C、 D、9. 以和为根的一元二次方程是( )A、 B、 C、 D、10. 等腰三角形的底边长为 , 周长为 , 则底角的正切值是( )A、 B、 C、 D、无法确定
A、44° B、66° C、56° D、46°8. 七年级一班同学组织了元旦联欢会,文艺委员准备在“横扫千军”“飞花令”“成语接龙”“看图猜诗词”四个项目中选择两个,则她选中“飞花令”和“看图猜诗词”的概率为( )A、 B、 C、 D、9. 以和为根的一元二次方程是( )A、 B、 C、 D、10. 等腰三角形的底边长为 , 周长为 , 则底角的正切值是( )A、 B、 C、 D、无法确定二、填空题:本题共6小题,每小题3分,共18分。
-
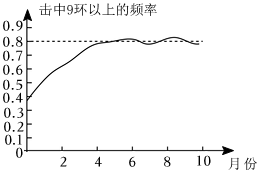
11. 点关于原点对称的点的坐标为 .12. 某射击运动员封闭训练个月,每天击中环以上的频率记录如图,封闭训练结束时,估计这名运动员射击一次时“击中环以上”的概率为 结果保留一位小数 .
 13. 关于的一元二次方程没有实数根,则的取值范围是 .14. 如图,已知与是公路弯道的外、内边线,它们有共同的圆心 , 所对的圆心角都是、、、在同一直线上,公路宽米,则弯道外侧边线比内侧边线多 米结果保留 .
13. 关于的一元二次方程没有实数根,则的取值范围是 .14. 如图,已知与是公路弯道的外、内边线,它们有共同的圆心 , 所对的圆心角都是、、、在同一直线上,公路宽米,则弯道外侧边线比内侧边线多 米结果保留 . 15. 在一个不透明纸箱中放有除了数字不同外,其它完全相同的2张卡片,分别标有数字1、2,从中任意摸出一张,放回搅匀后再任意摸出一张,两次摸出的数字之积为偶数的概率为 .16. 读一读:式子“”表示从开始的个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 , 这里“”是求和符号,通过对以上材料的阅读,计算 .
15. 在一个不透明纸箱中放有除了数字不同外,其它完全相同的2张卡片,分别标有数字1、2,从中任意摸出一张,放回搅匀后再任意摸出一张,两次摸出的数字之积为偶数的概率为 .16. 读一读:式子“”表示从开始的个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 , 这里“”是求和符号,通过对以上材料的阅读,计算 .三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
-
17. 如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,求图中阴影部分的面积.(结果保留π)
 18. 已知,如图,AD=BC.求证:AB=CD
18. 已知,如图,AD=BC.求证:AB=CD
 . 19. 如图,二次函数的图象与轴交于和两点,交轴于点 , 点、是二次函数图象上的一对对称点,一次函数的图象过点、 .
. 19. 如图,二次函数的图象与轴交于和两点,交轴于点 , 点、是二次函数图象上的一对对称点,一次函数的图象过点、 . (1)、求二次函数的解析式;
(1)、求二次函数的解析式;
(2)、根据图象直接写出使一次函数值大于二次函数值的的取值范围;
(3)、若直线与轴的交点为 , 连结、 , 求的面积.20. 某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:项目
第一年的工资万元
一年后的计算方法
基础工资
每年的增长率相同
住房补贴
每年增加
医疗费
固定不变
(1)、设基础工资每年增长率为 , 用含的代数式表示第三年的基础工资为万元;
(2)、某人在公司工作了年,他算了一下这年拿到的住房补贴和医疗费正好是这年基础工资总额的 , 问基础工资每年的增长率是多少?