云南省保山市腾冲市重点中学2023-2024学年九年级上学期数学月考考试试卷(12月)
试卷更新日期:2024-01-25 类型:月考试卷
一、单选题(每小题3分,共36分)
-
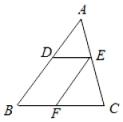
1. 已知⊙O的半径为3,点O到直线m的距离为d,若直线m与⊙O公共点的个数为2个,则d可取( )A、0 B、3 C、3.5 D、42. 已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E , 过点E作AB的平行线交BC于点F . 则下列说法不正确的是( )
 A、 B、 C、 D、3. 下列图形中,是中心对称图形的是( )A、
A、 B、 C、 D、3. 下列图形中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 将一元二次方程化为一元二次方程的一般形式,其中二次项系数为1,一次项系数和常数项分别是( )A、9、3 B、9、 C、、 D、、35. 已知二次函数 (a 为常数,且 )的图象上有三点则 的大小关系是( )A、 B、 C、 D、6. 事件①:任意画一个多边形,其外角和为360°;事件②:经过一个有交通信号灯的十字路口,遇到红灯;则下列说法正确的是( )A、事件①和②都是随机事件 B、事件①是随机事件,事件②是必然事件 C、事件①和②都是必然事件 D、事件①是必然事件,事件②是随机事件7. 如图,正六边形 内接于 ,正六边形的周长是12,则 的半径是( )
4. 将一元二次方程化为一元二次方程的一般形式,其中二次项系数为1,一次项系数和常数项分别是( )A、9、3 B、9、 C、、 D、、35. 已知二次函数 (a 为常数,且 )的图象上有三点则 的大小关系是( )A、 B、 C、 D、6. 事件①:任意画一个多边形,其外角和为360°;事件②:经过一个有交通信号灯的十字路口,遇到红灯;则下列说法正确的是( )A、事件①和②都是随机事件 B、事件①是随机事件,事件②是必然事件 C、事件①和②都是必然事件 D、事件①是必然事件,事件②是随机事件7. 如图,正六边形 内接于 ,正六边形的周长是12,则 的半径是( )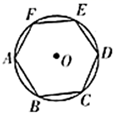 A、3 B、2 C、 D、8. 如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为( )
A、3 B、2 C、 D、8. 如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为( ) A、3 B、6 C、3π D、6π9. 某校随机抽查了10名参加2019年河南省初中学业水平考试学生的体育成绩,得到的结果如表:
A、3 B、6 C、3π D、6π9. 某校随机抽查了10名参加2019年河南省初中学业水平考试学生的体育成绩,得到的结果如表:成绩/分
46
47
48
49
50
人数/人
1
2
1
2
4
下列说法正确的是( )个.
A、这10名同学的体育成绩的众数为47 B、这10名同学的体育成绩的平均数为48 C、这10名同学的体育成绩的方差为50 D、这10名同学的体育成绩的中位数为4910. 为了疫情防控,某小区需要从甲、乙、丙、丁 4名志愿者中随机抽取2名负责该小区入口处的测温工作,则甲被抽中的概率是( )A、 B、 C、 D、11. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△EFC的位置,其中E、F分别是A、B的对应点,且点B在斜边EF上,直角边CE交AB于D,则旋转角等于( ). A、70° B、80° C、60° D、50°12. 如图,在中, , , , 动点从点开始沿向点以的速度移动,动点从点开始沿向点以的速度移动.若 , 两点分别从 , 两点同时出发,点到达点运动停止,则的面积随出发时间的函数关系图象大致是( )
A、70° B、80° C、60° D、50°12. 如图,在中, , , , 动点从点开始沿向点以的速度移动,动点从点开始沿向点以的速度移动.若 , 两点分别从 , 两点同时出发,点到达点运动停止,则的面积随出发时间的函数关系图象大致是( )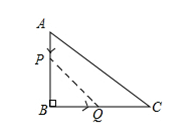 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(每小题2分,共8分)
-
13. 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为 .
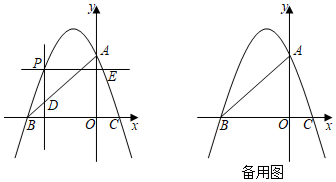
 14. 将抛物线y=x2向下平移3个单位,再向右平移2个单位后,所得抛物线的解析式为.15. 若m是方程的一个实数根,则 .16. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
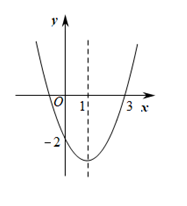
14. 将抛物线y=x2向下平移3个单位,再向右平移2个单位后,所得抛物线的解析式为.15. 若m是方程的一个实数根,则 .16. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b>0;②a﹣b+c=0;③当x<﹣1或x>3时,y>0;④一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根.
上述结论中正确的是 . (填上所有正确结论的序号)
三、解答题(第17、18题每小题7分,第19题4分,第20题8分,第21题7分,第22题5分,第23、24题每小题9分,共56分)
-
17. 不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个,蓝球1个.若从中任意摸出一个球,它是蓝球的概率为(1)、直接写出袋中黄球的个数;(2)、从袋子中一次摸2个球,请用画树状图或列表格的方法,求“取出至少一个红球”的概率.18. 已知二次函数的顶点坐标是 , 且过点 .(1)、求二次函数解析式.(2)、当时,求函数的取值范围.19. 解方程: .20. 观察下列等式:
第1个等式: ,
第2个等式: ,
第3个等式: ,
第4个等式: ,
按上述规律,回答以下问题:请写出第个等式: . .
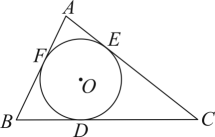
21. 如图, , 点P为内一点,连接 , 已知 . (1)、求证:;(2)、若 , 试求的值.22. 如图,⊙是的内切圆,D , E , F为切点,且 , 求 , , 的长.
(1)、求证:;(2)、若 , 试求的值.22. 如图,⊙是的内切圆,D , E , F为切点,且 , 求 , , 的长.