天津市河西区2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-01-25 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 已知 $⊙ O$ 的直径为 $15 c m$ ，若直线l与 $⊙ O$ 只有一个交点，那么圆心O到这条直线的距离为（）

A、 $7 c m$ B、 $7.5 c m$ C、 $8 c m$ D、 $10 c m$

查看试题解析
2. $2 s i n 60 °$ 的值等于（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
3. 下列是与中国航天事业相关的图标，可以看作是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 一个等边三角形的边长为2，则这个等边三角形的内切圆半径为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{\sqrt{3}}{3}$ D、 $\sqrt{3}$

查看试题解析
5. 如图，在 $△ A B C$ 中，若 $∠ C = 90 °$ ，则有（）

A、 $t a n A = \frac{a}{b}$ B、 $s i n A = \frac{b}{c}$ C、 $c o s A = \frac{a}{c}$ D、 $s i n A = \frac{a}{b}$

查看试题解析
6. 如图， $⊙ O$ 中弦AB ， CD相交于点P ， $∠ A = 42 °$ ， $∠ A P D = 77 °$ ，则 $∠ B$ 的度数为（）

A、 $43 °$ B、 $35 °$ C、 $34 °$ D、 $44 °$

查看试题解析
7. 一元二次方程 $4 x^{2} = 5 x - 1$ 的两根之和与两根之积分别为（）

A、 $\frac{5}{4}$ ， $\frac{1}{4}$ B、 $- \frac{5}{4}$ ， $\frac{1}{4}$ C、 $\frac{4}{5}$ ， $\frac{1}{4}$ D、 $- \frac{4}{5}$ ， $\frac{1}{4}$

查看试题解析
8. 抛物线 $y = x^{2} - 2 x - 3$ 与x轴的两个交点分别为（）

A、 $(3 ， 0)$ 和 $(- 1 ， 0)$ B、 $(- 3 ， 0)$ 和 $(1 ， 0)$ C、 $(2 ， 0)$ 和 $(- 4 ， 0)$ D、 $(4 ， 0)$ 和 $(- 2 ， 0)$

查看试题解析
9. 一个扇形的半径为 $24 c m$ ，面积是 $240 π c m^{2}$ ，则扇形的圆心角为（）

A、 $300 °$ B、 $240 °$ C、 $180 °$ D、 $150 °$

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ B A C = 120 °$ ，将 $△ A B C$ 绕点C逆时针旋转得到 $△ D E C$ ，点A ， B的对应点分别为D ， E ，连接AD ．当点A ， D ， E在同一条直线上时，下列结论一定正确的是（）

A、 $C B = C D$ B、 $∠ A B C = ∠ A D C$ C、 $A B ∥ C D$ D、 $D E + D C = B C$

查看试题解析
11. 如图，在 $△ A B C$ 中， $C A = C B = 4$ ， $∠ B A C = α$ ，将 $△ A B C$ 绕点A逆时针旋转 $2 α$ ，得到 $△ A B^{'} C^{'}$ ，连接 $B^{'} C$ 并延长交AB于点D ，当 $B^{'} D ⊥ A B$ 时， $\overset{⌢}{B B^{'}}$ 的长是（）

A、 $\frac{2 \sqrt{3}}{3} π$ B、 $\frac{4 \sqrt{3}}{3} π$ C、 $\frac{2 \sqrt{3}}{9} π$ D、 $\frac{8 \sqrt{3}}{9} π$

查看试题解析
12. 如图所示，是我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．如果大正方形面积为100，小正方形面积为4，则图中 $∠ θ$ 的正切值为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

13. 将点 $P (2 ， 6)$ 绕原点顺时针旋转 $180 °$ ，点P的对应点的坐标为．

查看试题解析
14. 不透明袋子中装有9个球，其中有7个绿球、2个白球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是绿球的概率是．

查看试题解析
15. 在 $R t △ A B C$ 中，若 $∠ C = 90 °$ ， $B C = \sqrt{3}$ ， $A C = 3$ ，则 $∠ A$ 的度数为．

查看试题解析
16. 若抛物线 $y = x^{2} - 6 x + k$ 与x轴没有交点，则实数k的值可以是．（写出一个即可）

查看试题解析
17. 如图，已知正方形ABCD的边长为2，以顶点C、D为圆心，2为半径的两弧交于点E ，点F为AB边的中点，连接EF ，则EF的长为．

查看试题解析
18. 如图，在每个小正方形边长为1的网格中，线段AB的端点A ， B均落在格点上．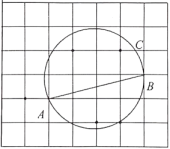
⑴线段AB的长等于；
⑵经过点A ， B的圆交网格线于点C ，在 $\overset{⌢}{A B}$ 上有一点E ，满足 $\overset{⌢}{C E} = \overset{⌢}{A B}$ ，请用无刻度的直尺，在如图所示的网格中，画出点E ，并简要说明点E的位置是如何找到的．（不要求证明）

查看试题解析

三、解答题（本大题共7小题，共66分。解答应写出文字说明、演算步骤或推理过程）

19. 解方程 $x^{2} - 6 x + 9 = (5 - 2 x)^{2}$ ．

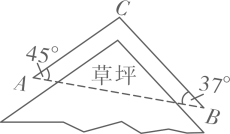
查看试题解析
20. 学生甲与学生乙学习概率初步知识后设计了如下游戏：学生甲手中有5、7、9三张扑克牌，学生乙手中有6、8、10三张扑克牌，每人从手中取出一张牌进行比较，数字小的为本局获胜．

(1)、若每人随机取手中的一张牌进行比赛，请列举出所有情况；

(2)、求学生乙本局获胜的概率．

查看试题解析
21. 请你结合题意，分别画出示意图，并完成解答：

(1)、在 $R t △ A B C$ 中，若 $∠ C = 90 °$ ，若 $∠ A = 30 °$ ， $A C = 3$ ，求AB的长；

(2)、在 $△ A B C$ 中， $A B = A C = 9$ ， $B C = 6$ ，求 $∠ C$ 的正弦．

查看试题解析
22. 小明上学途中要经过A，B两地，由于A，B两地之间有一片草坪，所以需要走路线AC，CB，如图，在△ABC中，AB=63m，∠A=45°，∠B=37°，求AC，CB的长．（结果保留小数点后一位）
参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， $\sqrt{2}$ 取1.414．

查看试题解析
23. 如图， $△ A B C$ 中， $A B = A C$ ， D为AC上一点，以CD为直径的 $⊙ O$ 与AB相切于点E ，交BC于点F ， $F G ⊥ A B$ ，垂足为G ．

(1)、求证：FG是 $⊙ O$ 的切线；

(2)、若 $⊙ O$ 的半径长为 $2 \sqrt{2}$ ， $B F = 3$ ，求BE的长．

查看试题解析
24. 如图，在菱形ABCD中， $∠ B = 60 °$ ， $A B = 2$ ，动点P从点A出发，以1单位长度/秒的速度沿折线 $B A \to A C$ 运动到点C ，同时动点Q从点A出发，以相同速度沿折线 $A C \to C D$ 运动到点D ，当一个点停止运动时，另一个点也随之停止．设 $△ A P Q$ 的面积为y ，运动时间为x秒．

(1)、当点P运动到AB的中点，求此时x的值和 $△ A P Q$ 的面积；

(2)、①当 $0 < x < 2$ 时，求y与x之间的函数关系式；
②当 $2 < x \leq 4$ 时，求y与x之间的函数关系式；

(3)、求在运动过程中 $△ A P Q$ 面积的最大值．（直接写出结果即可）

查看试题解析
25. 已知抛物线 $y = (x - n) (x - m)$ ，其中n ， m为常数，且 $n \neq m$ ．

(1)、若 $n = - 1$ ， $m = 3$ ，求抛物线的顶点坐标；

(2)、若抛物线的对称轴为 $x = 2$ ，且抛物线经过点 $(1 ， p)$ ．请你用含m的式子表示p ，并求出p的取值范围；

(3)、若 $n = 1$ ，点 $M (m ， 0)$ ，抛物线与y轴负半轴交于点G ，过点G作直线l平行于x轴，E是直线l上的动点，F是y轴上的动点， $E F = 2 \sqrt{2}$ ，点H是EF的中点，当MH的最小值是 $\frac{\sqrt{2}}{2}$ 时，求 $y = (x - n) (x - m)$ 在 $- 2 m - 1 \leq x \leq - 2 m$ 的图象的最低点的坐标．

查看试题解析