天津市河东区2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-01-25 类型:期末考试
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列说法正确的是( )A、“若是实数,则”是必然事件 B、成语“水中捞月”所描述的事件,是随机事件 C、“天津市明天降雨的概率为0.6”,表示天津市明天一定降雨 D、若抽奖活动的中奖概率为 , 则抽奖50次必中奖1次2. 一元二次方程根的判别式的值是( )A、33 B、23 C、17 D、3. 在平面直角坐标系中,点关于原点对称的点的坐标是( )A、 B、 C、 D、4. 我国古代数学的许多创新与发明都曾在世界上有重要影响,下列图形“杨辉三角”“中国七巧板”“刘徽割圆术”“赵爽弦图”中,中心对称图形是( )A、
 B、
B、 C、
C、 D、
D、 5. 对于抛物线 , 下列说法错误的是( )A、开口向上 B、对称轴是直线 C、时,随的增大而减小 D、 , 函数有最小值6. 如图,是的直径.若 , , 则长等于( )
5. 对于抛物线 , 下列说法错误的是( )A、开口向上 B、对称轴是直线 C、时,随的增大而减小 D、 , 函数有最小值6. 如图,是的直径.若 , , 则长等于( ) A、 B、 C、4 D、57. 一个扇形的弧长是 , 面积为 , 则其半径为( )A、6 B、12 C、36 D、1448. 某种品牌手机经过两次降价,每部售价由2000元降到1620元,则平均每次降价的百分率为( )A、 B、 C、 D、9. 已知点 , , 都在函数的图象上,则( )A、 B、 C、 D、10. 如图,已知点是外一点,用直尺和圆规过点作一条直线,使它与相切于点.下面是忠忠给出的两种作法:
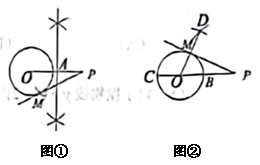
A、 B、 C、4 D、57. 一个扇形的弧长是 , 面积为 , 则其半径为( )A、6 B、12 C、36 D、1448. 某种品牌手机经过两次降价,每部售价由2000元降到1620元,则平均每次降价的百分率为( )A、 B、 C、 D、9. 已知点 , , 都在函数的图象上,则( )A、 B、 C、 D、10. 如图,已知点是外一点,用直尺和圆规过点作一条直线,使它与相切于点.下面是忠忠给出的两种作法:作法Ⅰ:如图①,作线段的垂直平分线交于点:以点为圆心,长为半径画弧交于点 , 作直线.直线即为所求.
作法Ⅱ:如图②,连接 , 交于点 , 作直径 , 以为圆心,长为半径作弧:以为圆心,长为半径作弧,两弧相交于点 , 连接 , 交于点 , 作直线.直线即为所求.对于忠忠的两种作法,下列说法正确的是( )
 A、两种作法都正确 B、两种作法都错误 C、作法Ⅰ正确,作法Ⅱ错误 D、作法Ⅱ正确,作法Ⅰ错误11. 如图,点是正方形的边上一点,将绕着顶点逆时针旋转 , 得 , 连接 , 若为的中点,则下列结论正确的是( )
A、两种作法都正确 B、两种作法都错误 C、作法Ⅰ正确,作法Ⅱ错误 D、作法Ⅱ正确,作法Ⅰ错误11. 如图,点是正方形的边上一点,将绕着顶点逆时针旋转 , 得 , 连接 , 若为的中点,则下列结论正确的是( ) A、 B、 C、 D、12. 约定:若函数图象上至少存在不同的两点关于原点对称,则把该函数称为“黄金函数”,其图象上关于原点对称的两点叫做一对“黄金点”.若点 , 是关于的“黄金函数”上的一对“黄金点”,且该函数的对称轴始终位于直线的右侧;则下列结论:①;②:③;④ , 正确的是( )A、①②③ B、①②④ C、②③④ D、①③④
A、 B、 C、 D、12. 约定:若函数图象上至少存在不同的两点关于原点对称,则把该函数称为“黄金函数”,其图象上关于原点对称的两点叫做一对“黄金点”.若点 , 是关于的“黄金函数”上的一对“黄金点”,且该函数的对称轴始终位于直线的右侧;则下列结论:①;②:③;④ , 正确的是( )A、①②③ B、①②④ C、②③④ D、①③④二、填空题(本大题共6小题,每小题3分,共18分)
-
13. 一个不透明的袋子里装有2个绿球、3个黑球和6个红球,它们除颜色外其余相同.从袋中任意摸出一个球为绿球的概率为.14. 若方程的一个根是 , 则另一个根是 .15. 已知一元二次方程的两根为 , , 则.16. 抛物线与轴只有一个公共点,则的值为.17. 图①、图②均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点、、、、均为格点,只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹.
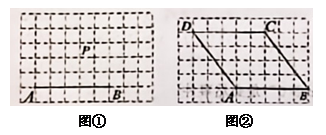
⑴在图①中,作以点为对称中心的平行四边形;
⑵在图②中,在四边形的边上找一点 , 连结 , 使 ,
18. 已知,矩形中, , , 为边上一动点,以为边构造等边(点位于下方),连接.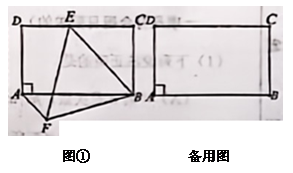
⑴如图①,当时,;
⑵点在运动的过程中,的最小值为.
三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程)
-
19. 解下列方程:(1)、;(2)、.20. 从同一副扑克牌中选出四张牌,牌面数字分别为2,5,6,8.将这四张牌背面朝上,洗匀.(1)、从这四张牌中随机抽出一张牌,求这张牌上的牌面数字是偶数的概率:(2)、小明从这四张牌中随机抽出一张牌,记下牌面数字后,放回.背面朝上,洗匀.然后,小华从中随机抽出一张牌,请用画树状图或列表的方法,求小华抽出的牌上的牌面数字比小明抽出的牌上的牌面数字大的概率.21. 已知正方形的边长为2,为原点.
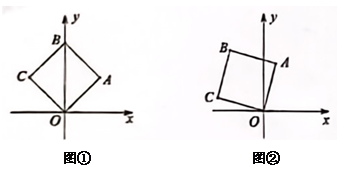 (1)、如图①,若点在轴上,求点的坐标:(2)、如图②,将图①中的正方形绕点逆时针旋转时,求点的坐标.22. 已知是的直径,弦于点 , 连接.
(1)、如图①,若点在轴上,求点的坐标:(2)、如图②,将图①中的正方形绕点逆时针旋转时,求点的坐标.22. 已知是的直径,弦于点 , 连接. (1)、如图①,若 , , 求的长;(2)、如图②,是弧上一点, , 的延长线交于点 , 若 , 求的度数.23. 落实五育并举,加强劳动教育,某中学在当地政府的支持下,建成了一处劳动实践基地.2024年计划将其中的土地全部种植甲乙两种蔬菜,经调查发现:甲种蔬菜成本为50元.乙种蔬菜的种植成本与其种植面积之间的关系如下图所示.设乙种蔬菜种植成本为(元),乙种蔬菜的植面积为(其中).
(1)、如图①,若 , , 求的长;(2)、如图②,是弧上一点, , 的延长线交于点 , 若 , 求的度数.23. 落实五育并举,加强劳动教育,某中学在当地政府的支持下,建成了一处劳动实践基地.2024年计划将其中的土地全部种植甲乙两种蔬菜,经调查发现:甲种蔬菜成本为50元.乙种蔬菜的种植成本与其种植面积之间的关系如下图所示.设乙种蔬菜种植成本为(元),乙种蔬菜的植面积为(其中). (1)、根据题意,填写下表:
(1)、根据题意,填写下表:种植面积
200
400
500
600
700
乙种蔬菜种植成本(元)
20
①
②
40
③
(2)、设2024年甲乙两种蔬菜总种植成本为元,如何分配两种蔬菜的种植面积,使最小?
