备战2024年中考数学细点逐一突破真题训练第14章锐角三角函数及其应用
试卷更新日期:2024-01-25 类型:一轮复习
一、实数的运算
-
1. 计算: .2. 计算: .3. 计算:
二、特殊角的三角函数值
-
4. 如图,在中, , 是的中点, , 交于 , 若 , 则.
 5. 如图,在正方形中,是的中点, , 求的值.
5. 如图,在正方形中,是的中点, , 求的值. 6. 如图,在网格中小正方形的边长均为1,△ABC的顶点都在格点上,则等于( )
6. 如图,在网格中小正方形的边长均为1,△ABC的顶点都在格点上,则等于( )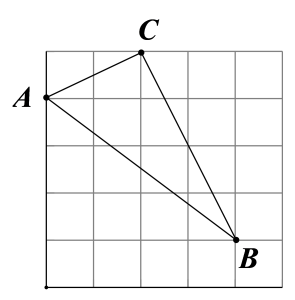 A、 B、 C、 D、7. 如图,在中, , 点在边上, , , , 求的长.
A、 B、 C、 D、7. 如图,在中, , 点在边上, , , , 求的长. 8. 如图,3个大小完全相同的正六边形无缝隙、不重叠的拼在一起,连接正六边形的三个顶点得到 , 则的值是 .
8. 如图,3个大小完全相同的正六边形无缝隙、不重叠的拼在一起,连接正六边形的三个顶点得到 , 则的值是 .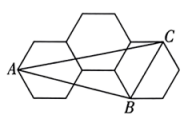 9. 如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD , 相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF , ③和④分别是Rt△CDG和Rt△DAH , ⑤是正方形EFGH , 直角顶点E , F , G , H分别在边BF , CG , DH , AE上.
9. 如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD , 相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF , ③和④分别是Rt△CDG和Rt△DAH , ⑤是正方形EFGH , 直角顶点E , F , G , H分别在边BF , CG , DH , AE上. (1)、若EF=3cm , AE+FC=11cm , 则BE的长是 cm .(2)、若 , 则tan∠DAH的值是 .
(1)、若EF=3cm , AE+FC=11cm , 则BE的长是 cm .(2)、若 , 则tan∠DAH的值是 .三、拥抱型-实际应用
-
10. 日照间距系数反映了房屋日照情况,如图①,当前后房屋都朝向正南时,日照间距系数 ,其中 为楼间水平距离, 为南侧楼房高度, 为北侧楼房底层窗台至地面高度.如图②,山坡 朝北, 长为 ,坡度为 ,山坡顶部平地 上有一高为 的楼房 ,底部 到 点的距离为 .
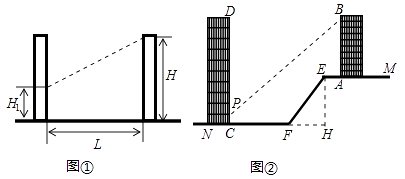 (1)、求山坡 的水平宽度 ;(2)、欲在 楼正北侧山脚的平地 上建一楼房 ,已知该楼底层窗台 处至地面 处的高度为 ,要使该楼的日照间距系数不低于 ,底部 距 处至少多远?
(1)、求山坡 的水平宽度 ;(2)、欲在 楼正北侧山脚的平地 上建一楼房 ,已知该楼底层窗台 处至地面 处的高度为 ,要使该楼的日照间距系数不低于 ,底部 距 处至少多远?
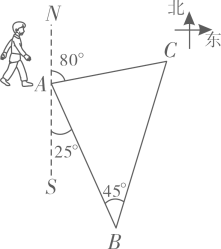
11. 为了增强学生体质、针炼学生意志,某校组织一次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为点和点,行进路线为.点在点的南偏东方向处,点在点的北偏东方向,行进路线AB和BC所在直线的夹角为.⑴求行进路线BC和CA所在直线的夹角的度数;
⑵求检查点和之间的距离(结果保留根号).
 12. 如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.
12. 如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2. (1)、求加固后坝底增加的宽度AF的长;(2)、求完成这项工程需要土石多少立方米?
(1)、求加固后坝底增加的宽度AF的长;(2)、求完成这项工程需要土石多少立方米?四、背靠背型-实际应用
-
13. 小亮周末到公园散步,当他沿着一段平坦的直线跑道行走时,前方出现一棵树AC和一栋楼房BD,如图,假设小亮行走到F处时正好通过树顶C看到楼房的E处,此时 , 已知树高米,楼房米,E处离地面25米.
 (1)、求树与楼房之间的距离AB的长;(2)、小亮再向前走多少米从树顶刚好看不到楼房BD?(结果保留根号)14. 我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔,是苏北地区现存最高和最古老的宝塔.小明与小亮要测量阿育王塔的高度,如图所示,小明在点 处测得阿育王塔最高点 的仰角 ,再沿正对阿育王塔方向前进至 处测得最高点 的仰角 , ;小亮在点 处竖立标杆 ,小亮的所在位置点 、标杆顶 、最高点 在一条直线上, , .
(1)、求树与楼房之间的距离AB的长;(2)、小亮再向前走多少米从树顶刚好看不到楼房BD?(结果保留根号)14. 我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔,是苏北地区现存最高和最古老的宝塔.小明与小亮要测量阿育王塔的高度,如图所示,小明在点 处测得阿育王塔最高点 的仰角 ,再沿正对阿育王塔方向前进至 处测得最高点 的仰角 , ;小亮在点 处竖立标杆 ,小亮的所在位置点 、标杆顶 、最高点 在一条直线上, , . (1)、求阿育王塔的高度 ;(2)、求小亮与阿育王塔之间的距离 .
(1)、求阿育王塔的高度 ;(2)、求小亮与阿育王塔之间的距离 .(注:结果精确到 ,参考数据: , , )
五、母子型-实际应用
-
15. 如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成如图2,是灯杆,是灯管支架,灯管支架与灯杆间的夹角.综合实践小组的同学想知道灯管支架的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得m,m(A,E,F在同一条直线上).根据以上数据,解答下列问题:
 (1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).16. 年月日点分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面处发射,当飞船到达点时,从位于地面处的雷达站测得的距离是 , 仰角为;后飞船到达处,此时测得仰角为 .
(1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).16. 年月日点分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面处发射,当飞船到达点时,从位于地面处的雷达站测得的距离是 , 仰角为;后飞船到达处,此时测得仰角为 .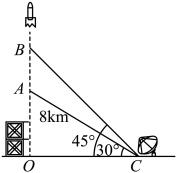 (1)、求点离地面的高度;(2)、求飞船从处到处的平均速度.(结果精确到 , 参考数据:)17. 综合与实践
(1)、求点离地面的高度;(2)、求飞船从处到处的平均速度.(结果精确到 , 参考数据:)17. 综合与实践【问题情境】南宁青秀山龙象塔始建于明代万历年间,塔呈八角形,九级重檐结构,是青秀山的地标建筑.在一次数学综合实践活动中,李老师布置了一个任务:请根据所学知识设计一种方案,测量龙象塔的高.
 (1)、【实践探究】某小组通过思考,绘制了如图2所示的测量示意图,即在水平地面上的点C处测得塔顶端A的仰角为 , 点C到点B的距离米,即可得出塔高米(请你用所给数据和a表示).(2)、【问题解决】但在实践中发现:由于无法直接到达塔底端的B点,因此BC无法直接测量.该小组对测量方案进行了如下修改:如图3,从水平地面的C点向前走a米到达点D处后,在D处测得塔顶端A的仰角为 , 即可通过计算求得塔高AB.若测得的 , , 米,请你利用所测数据计算塔高AB.(计算结果精确到1米,参考数据: , )
(1)、【实践探究】某小组通过思考,绘制了如图2所示的测量示意图,即在水平地面上的点C处测得塔顶端A的仰角为 , 点C到点B的距离米,即可得出塔高米(请你用所给数据和a表示).(2)、【问题解决】但在实践中发现:由于无法直接到达塔底端的B点,因此BC无法直接测量.该小组对测量方案进行了如下修改:如图3,从水平地面的C点向前走a米到达点D处后,在D处测得塔顶端A的仰角为 , 即可通过计算求得塔高AB.若测得的 , , 米,请你利用所测数据计算塔高AB.(计算结果精确到1米,参考数据: , )六、生活情境应用
-
18. 图1是小明在健身器材上进行仰卧起坐锻炼时情景.
图2是小明锻炼时上半身由EM位置运动到与地面垂直的EN位置时的示意图.
已知BC=0.64米,AD=0.24米,AB=1.30米.
 (1)、求AB的倾斜角α的度数(精确到x);(2)、若测得EN=0.85米,试计算小明头顶由M点运动到N点的路径的长度.(精确到0.01米)19. 图1是某越野车的侧面示意图,折线段表示车后盖,已知 , , , 该车的高度 . 如图2,打开后备箱,车后盖落在处,与水平面的夹角 .
(1)、求AB的倾斜角α的度数(精确到x);(2)、若测得EN=0.85米,试计算小明头顶由M点运动到N点的路径的长度.(精确到0.01米)19. 图1是某越野车的侧面示意图,折线段表示车后盖,已知 , , , 该车的高度 . 如图2,打开后备箱,车后盖落在处,与水平面的夹角 . (1)、求打开后备箱后,车后盖最高点到地面的距离;(2)、若小琳爸爸的身高为 , 他从打开的车后盖处经过,有没有碰头的危险?请说明理由.
(1)、求打开后备箱后,车后盖最高点到地面的距离;(2)、若小琳爸爸的身高为 , 他从打开的车后盖处经过,有没有碰头的危险?请说明理由.(结果精确到 , 参考数据: , , , )
20. 如图所示,在某交叉路口,一货车在道路①上点A处等候“绿灯”一辆车从被山峰遮挡的道路②上的点B处由南向北行驶.已知 , , 线段的延长线交直线于点D.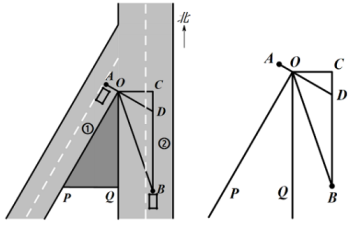 (1)、求的大小;(2)、若在点B处测得点O在北偏西方向上,其中米.问该轿车至少行驶多少米才能发现点A处的货车?(当该轿车行驶至点D处时,正好发现点A处的货车)21. 图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,摄像头高度 , 识别的最远水平距离。
(1)、求的大小;(2)、若在点B处测得点O在北偏西方向上,其中米.问该轿车至少行驶多少米才能发现点A处的货车?(当该轿车行驶至点D处时,正好发现点A处的货车)21. 图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,摄像头高度 , 识别的最远水平距离。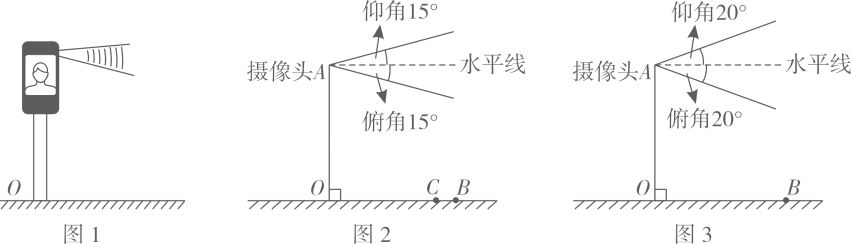 (1)、身高的小杜,头部高度为 , 他站在离摄像头水平距离的点C处,请问小杜最少需要下蹲多少厘米才能被识别。(2)、身高的小若,头部高度为 , 踮起脚尖可以增高 , 但仍无法被识别.社区及时将摄像头的仰角、俯角都调整为(如图3),此时小若能被识别吗?请计算说明。
(1)、身高的小杜,头部高度为 , 他站在离摄像头水平距离的点C处,请问小杜最少需要下蹲多少厘米才能被识别。(2)、身高的小若,头部高度为 , 踮起脚尖可以增高 , 但仍无法被识别.社区及时将摄像头的仰角、俯角都调整为(如图3),此时小若能被识别吗?请计算说明。(精确到 , 参考数据)
22. 公园草坪上有一架秋千 , 秋千静止时,底端到地面的距离为 , 从坚直位置开始,向右可摆动的最大夹角为 , 已知秋千的长 . (1)、如图1,当向右摆动到最大夹角时,求到地面的距离;(2)、如图2,若有人在点右侧搭建了一个等腰帐篷,已知 , 帐篷的高为 , 秋千摆动的过程中是否会撞到帐篷?若不会撞到,请说明理由;若会撞到,则帐篷应该向右移动超过多少米才能不被撞到?23. 图1是某款篮球架,图2是其示意图,立柱垂直地面 , 支架与交于点 , 支架交于点 , 支架平行地面 , 篮筐与支架在同一直线上,米,米,.
(1)、如图1,当向右摆动到最大夹角时,求到地面的距离;(2)、如图2,若有人在点右侧搭建了一个等腰帐篷,已知 , 帐篷的高为 , 秋千摆动的过程中是否会撞到帐篷?若不会撞到,请说明理由;若会撞到,则帐篷应该向右移动超过多少米才能不被撞到?23. 图1是某款篮球架,图2是其示意图,立柱垂直地面 , 支架与交于点 , 支架交于点 , 支架平行地面 , 篮筐与支架在同一直线上,米,米,.
 (1)、求的度数.(2)、某运动员准备给篮筐挂上篮网,如果他站在凳子上,最高可以把篮网挂到离地面3米处,那么他能挂上篮网吗?请通过计算说明理由.
(1)、求的度数.(2)、某运动员准备给篮筐挂上篮网,如果他站在凳子上,最高可以把篮网挂到离地面3米处,那么他能挂上篮网吗?请通过计算说明理由.(参考数据:)
七、跨学科背景应用
-
24. 如图,光从空气斜射入水中,入射光线射到水池的水面B点后折射光线射到池底点D处,入射角 , 折射角;入射光线射到水池的水面C点后折射光线射到池底点E处,入射角 , 折射角 . , 、为法线.入射光线、和折射光线、及法线、都在同一平面内,点A到直线的距离为6米.
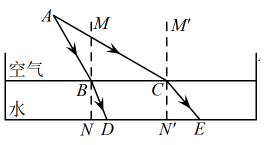 (1)、求的长;(结果保留根号)(2)、如果米,求水池的深.(参考数据:取1.41,取1.73,取0.37,取0.93,取0.4,取0.65,取0.76,取0.85)25. 如图是某风车平面示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片 , 此时各叶片影子在点M右侧形成线段 , O的对应点为D,测得 , 此时太阳的与地面的夹角为(即).
(1)、求的长;(结果保留根号)(2)、如果米,求水池的深.(参考数据:取1.41,取1.73,取0.37,取0.93,取0.4,取0.65,取0.76,取0.85)25. 如图是某风车平面示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片 , 此时各叶片影子在点M右侧形成线段 , O的对应点为D,测得 , 此时太阳的与地面的夹角为(即). (1)、求旋转中心到地面的距离的值.(2)、风车转动时,要求叶片外端离地面的最低高度高于米,请判断此风车是否符合要求.26. 问题:如何设计“倍力桥”的结构?
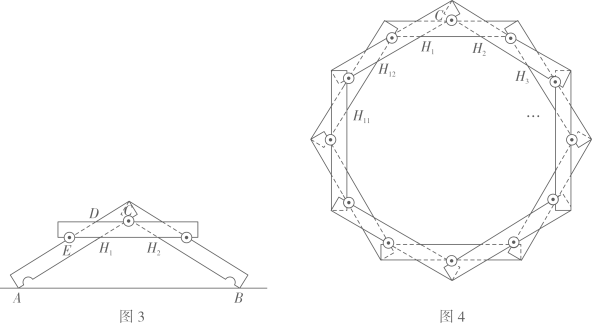
(1)、求旋转中心到地面的距离的值.(2)、风车转动时,要求叶片外端离地面的最低高度高于米,请判断此风车是否符合要求.26. 问题:如何设计“倍力桥”的结构?图1是搭成的“倍力桥”,纵梁a,c夹住横梁 , 使得横梁不能移动,结构稳固.
图2是长为 , 宽为的横梁侧面示意图,三个凹槽都是半径为的半圆.圆心分别为 , 纵梁是底面半径为的圆柱体.用相同规格的横梁、纵梁搭“桥”,间隙忽略不计.


探究1:图3是“桥”侧面示意图,A,B为横梁与地面的交点,C,E为圆心,D,H1 , H2是横梁侧面两边的交点.测得AB=32cm,点C到AB的距离为12cm.试判断四边形CDEH1的形状,并求的值.
探究2:若搭成的“桥”刚好能绕成环,其侧面示意图的内部形成一个多边形.
①若有12根横梁绕成环,图4是其侧面示意图,内部形成十二边形 , 求的值;
②若有n根横梁绕成的环(n为偶数,且n≥6),试用关于n的代数式表示内部形成的多边形的周长.
八、几何综合应用
-
27. 如图,已知是的直径,是的弦,点是外的一点, , 垂足为点 , 与相交于点 , 连接 , 且 , 延长交的延长线于点 .
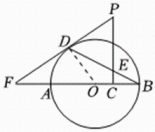 (1)、求证:是的切线;(2)、若 , , , 求的长.
(1)、求证:是的切线;(2)、若 , , , 求的长.

