山西省晋中市寿阳县2023-2024学年九年级上学期数学月考考试试卷(12月)
试卷更新日期:2024-01-25 类型:月考试卷
一、选择题(本大题共10个小题,每小题3分,共30分。在每个小题给出的四个选项中,只有一项符合题目要求,把正确答案的标号用2B铅笔填(涂)在答题卡内相应的位置上)
-
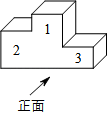
1. 在△ABC中,∠C=90°,sinA= , 则∠B的度数为( )A、30° B、45° C、60° D、75°2. 下列各点中,在反比例函数y=图象上的是( )A、(﹣1,8) B、(﹣2,4) C、(1,7) D、(2,4)3. 运动会的领奖台可以近似的看成如图所示的立体图形,则它的左视图是( )
 A、
A、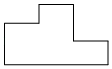 B、
B、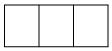 C、
C、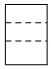 D、
D、 4. 如图,A是反比例函数图象上第二象限内的一点,若△ABO的面积为4,则的值为( )
4. 如图,A是反比例函数图象上第二象限内的一点,若△ABO的面积为4,则的值为( ) A、8 B、﹣8 C、4 D、-45. 下列叙述正确的是( )A、任意两个等腰三角形相似 B、任意两个平行四边形相似 C、任意两个矩形相似 D、任意两个正方形相似6. 如图,在平面直角坐标系中,已知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A'的坐标是( )
A、8 B、﹣8 C、4 D、-45. 下列叙述正确的是( )A、任意两个等腰三角形相似 B、任意两个平行四边形相似 C、任意两个矩形相似 D、任意两个正方形相似6. 如图,在平面直角坐标系中,已知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A'的坐标是( )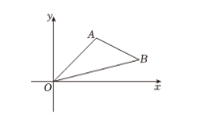 A、(1,1) B、(4,4)或(8,2) C、(4,4) D、(4,4)或(-4,-4)7. 如图,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
A、(1,1) B、(4,4)或(8,2) C、(4,4) D、(4,4)或(-4,-4)7. 如图,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( ) A、1:4 B、1:3 C、1:2 D、2:38. 反比例函数的图象在第一、三象限,点A(﹣2,)、B(4,)、C(5,)是图象上的三点,则的大小关系是( )A、 B、 C、 D、9. 如图,某一时刻太阳光下,小明测得一棵树落在地面上的影子长为2.8米,落在墙上的影子高为1.2米,同一时刻同一地点,身高1.6米他在阳光下的影子长0.4米,则这棵树的高为( )米.
A、1:4 B、1:3 C、1:2 D、2:38. 反比例函数的图象在第一、三象限,点A(﹣2,)、B(4,)、C(5,)是图象上的三点,则的大小关系是( )A、 B、 C、 D、9. 如图,某一时刻太阳光下,小明测得一棵树落在地面上的影子长为2.8米,落在墙上的影子高为1.2米,同一时刻同一地点,身高1.6米他在阳光下的影子长0.4米,则这棵树的高为( )米. A、6.2 B、10 C、11.2 D、12.410. 如果一个等腰三角形的顶角为36°,那么其底边与腰之比等于 , 我们把这样的等腰三角形称为黄金三角形.如图,在△ABC中,AB=AC=1,∠A=36°,△ABC看作第一个黄金三角形;作∠ABC的平分线BD,交AC于点D,△BCD看作第二个黄金三角形;作∠BCD的平分线CE,交BD于点E,△CDE看作第三个黄金三角形;…以此类推,第2023个黄金三角形的腰长是( )
A、6.2 B、10 C、11.2 D、12.410. 如果一个等腰三角形的顶角为36°,那么其底边与腰之比等于 , 我们把这样的等腰三角形称为黄金三角形.如图,在△ABC中,AB=AC=1,∠A=36°,△ABC看作第一个黄金三角形;作∠ABC的平分线BD,交AC于点D,△BCD看作第二个黄金三角形;作∠BCD的平分线CE,交BD于点E,△CDE看作第三个黄金三角形;…以此类推,第2023个黄金三角形的腰长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共15分)
-
11. 反比例函数的图象在二、四象限,则应满足 .12. 如图,点P在△ABC的边AC上,要使△ABP∽△ACB,添加一个条件 .
 13. 从某个方向观察一个正六棱柱,可看到如图所示的图形,其中四边形ABCD为矩形,E、F分别是AB、DC的中点.若AD=8,AB=6,则这个正六棱柱的侧面积为; .
13. 从某个方向观察一个正六棱柱,可看到如图所示的图形,其中四边形ABCD为矩形,E、F分别是AB、DC的中点.若AD=8,AB=6,则这个正六棱柱的侧面积为; . 14. 如图,在平面直角坐标系中,点A,B分别在反比例函数和的图象上,且AB∥轴,若 , 则的值为 .
14. 如图,在平面直角坐标系中,点A,B分别在反比例函数和的图象上,且AB∥轴,若 , 则的值为 . 15. 如图,在正方形中, , 延长至 , 使 , 连接 , 平分交于 , 连接 , 则的长为 .
15. 如图,在正方形中, , 延长至 , 使 , 连接 , 平分交于 , 连接 , 则的长为 .
三、解答题:本大题共8小题,共75分.解答时,应写出必要的文字说明、证明过程或演算步骤.
-
16. 解方程或计算(1)、解方程:;(2)、解方程:(3)、计算:(4)、计算:17. 如图,△ABC的顶点都在网格点上,点B的坐标(-2,1)
 (1)、以点O为位似中心,把△ABC按2:1放大在y轴的左侧,画出放大后的△DEF;
(1)、以点O为位似中心,把△ABC按2:1放大在y轴的左侧,画出放大后的△DEF;
(2)、点A的对应点D的坐标是 ;
(3)、= .18. 如图,在平行四边形ABCD中,过点B作BE⊥CD于E,F为AE上一点,且∠BFE=∠C. (1)、求证:△ABF∽△EAD;
(1)、求证:△ABF∽△EAD;
(2)、若AB=3,AD=2,∠BAE=30°,求BF的长.19. 如图,一次函数的图与反比例函数的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D. (1)、求这两个函数的解析式;(2)、求△ADC的面积;(3)、根据图象直接写出不等式的解集.20. 阅读与思考
(1)、求这两个函数的解析式;(2)、求△ADC的面积;(3)、根据图象直接写出不等式的解集.20. 阅读与思考
下面是小宇同学的一篇日记,请仔细阅读并完成相应的任务. 在物理活动课上,我们“博学”小组的同学,参加了一次“探究电功率P与电阻R之间的函数关系”的活动.
在物理活动课上,我们“博学”小组的同学,参加了一次“探究电功率P与电阻R之间的函数关系”的活动.
第一步,实验测量.根据物理知识,改变电阻R的大小,通过测量电路中的电流,计算电功率P.
第二步,整理数据.R/Ω
…
3
6
9
12
15
…
P/W
…
3
1.5
1
0.75
0.7
…
第三步,描点连线.以R的数值为横坐标,对应P的数值为纵坐标在平面直角坐标系中描出以表中数值为坐标的各点,并用光滑的曲线顺次连接这些点.
在数据分析时,我发现一个数据有错误,重新测量计算后,证明了我的猜想正确,并修改了表中这个数据.实验结束后,大家都有很多收获,每人都撰写了日记.任务:
(1)、表格中错误的数据是 , P与R的函数表达式为;(2)、在平面直角坐标系中,画出P与R的函数图象; (3)、结合图象,直接写出P大于6W时R的取值范围.21. 通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.
(3)、结合图象,直接写出P大于6W时R的取值范围.21. 通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影. (1)、【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);
(1)、【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);
(2)、【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为____ ;
A、
B、
B、
C、
C、
D、
D、
(3)、【解决问题】如图③,河对岸有一灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向前进到达点F处测得自己的影长FG=4m.已知小明的身高为1.6m,求灯杆AB的高度.22. 【定义】平面直角坐标系内的直角三角形如果满足以下两个条件:①两直角边平行于坐标轴;②斜边的两个顶点在同一反比例函数图象上.那么我们把这个直角三角形称为该反比例函数的“伴随直角三角形”.
(3)、【解决问题】如图③,河对岸有一灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向前进到达点F处测得自己的影长FG=4m.已知小明的身高为1.6m,求灯杆AB的高度.22. 【定义】平面直角坐标系内的直角三角形如果满足以下两个条件:①两直角边平行于坐标轴;②斜边的两个顶点在同一反比例函数图象上.那么我们把这个直角三角形称为该反比例函数的“伴随直角三角形”.例如,在图中,Rt△ABC的边BC∥x轴,AC∥y轴,且点A,B在反比例函数
的图象上,则Rt△ABC是反比例函数的“伴随直角三角形”.
 (1)、【理解】在Rt△ABC中,∠C=90°,点A,B,C的坐标分别为
(1)、【理解】在Rt△ABC中,∠C=90°,点A,B,C的坐标分别为①A(3,4),B(6,2),C(6,4);
②A(3,1),B(2,2),C(2,1);
③A(﹣1,2),B(1,﹣2),C(1,2).
其中可能是某反比例函数的“伴随直角三角形”的是;(填序号)
(2)、【应用】已知点C(2,﹣3)是反比例函数的“伴随直角三角形”的直角顶点,求直线AB的函数表达式;(3)、【提升】Rt△ABC是反比例函数的“伴随直角三角形”,且点A的坐标为(﹣4,﹣1),点B的坐标为(﹣1,﹣4).若△ABC平移后得到的△A'B'C',且△A'B'C'是反比例函数的“伴随直角三角形”,分别求点A',B'的坐标.23. 如图1,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴负半轴、y轴正半轴上,AB、BC的长分别是方程的两个根. (1)、求点B的坐标;
(1)、求点B的坐标;
(2)、如图2,过点A且垂直于AC的直线交轴于点F,在直线AF上截取AD=AC,过点D作DE⊥轴于点E,求经过点D的反比例函数的关系式;(3)、在(2)的条件下,在y轴上是否存在一点P,使以D,E,P为顶点的三角形与△OAC相似?若存在,求出点P的坐标;若不存在,请说明理由.