重庆市潼南区六校2023-2024学年九年级上学期数学第二次月考考试试卷
试卷更新日期:2024-01-25 类型:月考试卷
一、单选题:(本大题10个小题,每小题4分,共40分)
-
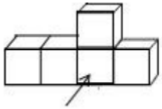
1. -5的相反数是( )A、5 B、-5 C、 D、2. 如图是一个由5个相同正方体组成的立体图形,从前面看得到的图形是( )
 A、
A、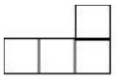 B、
B、 C、
C、 D、
D、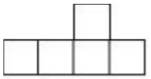 3. 如图,直线 , , 若 , 则∠CAF的度数为( )
3. 如图,直线 , , 若 , 则∠CAF的度数为( )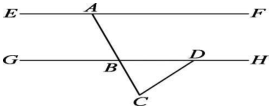 A、35° B、45° C、55° D、65°4. 已知m是一元二次方程的一个根,则的值是( )A、-2023 B、2023 C、2022 D、20245. 抛物线 的对称轴是( )A、直线 B、直线 C、直线 D、直线6. 如图,每个图形都由同样大小的“△”按照一定的规律组成,其中第1个图形有5个“△”,第2个图形有10个“△”,第3个图形有15个“△”,…,则第8个图形中“△”的个数为( )
A、35° B、45° C、55° D、65°4. 已知m是一元二次方程的一个根,则的值是( )A、-2023 B、2023 C、2022 D、20245. 抛物线 的对称轴是( )A、直线 B、直线 C、直线 D、直线6. 如图,每个图形都由同样大小的“△”按照一定的规律组成,其中第1个图形有5个“△”,第2个图形有10个“△”,第3个图形有15个“△”,…,则第8个图形中“△”的个数为( )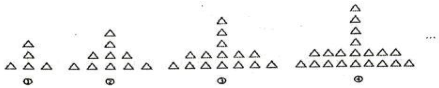 A、40 B、42 C、44 D、467. 估计的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间8. 如图,AB是O的直径,C为O上一点,连接AC、BC , 于点E , CD是O的切线,且 , 若 , , 则CD的长为( )
A、40 B、42 C、44 D、467. 估计的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间8. 如图,AB是O的直径,C为O上一点,连接AC、BC , 于点E , CD是O的切线,且 , 若 , , 则CD的长为( ) A、 B、5 C、 D、49. 如图,在矩形ABCD中,以点A为圆心AD为半径顺时针旋转线段AD交AC于E , 以点C为圆心CB为半径顺时针旋转线段CB交AC于F , 连接DE、BF , 若 , 则∠ABF一定为( )
A、 B、5 C、 D、49. 如图,在矩形ABCD中,以点A为圆心AD为半径顺时针旋转线段AD交AC于E , 以点C为圆心CB为半径顺时针旋转线段CB交AC于F , 连接DE、BF , 若 , 则∠ABF一定为( )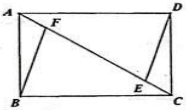 A、 B、 C、 D、10. 学习添括号法则后,小明所在的学习小组为了加强对法则的理解,编了一个小游戏,游戏规则如下:把多项式看做a , , , , 五项的和,这五项可以依序循环站位,例如:当a站在第2位时,站在第一位,变为多项式 . 在任意相邻两个或三个字母左右添括号,再在符号不变的情况下,交换括号前后两字母的位置,则称此操作为“交换操作”,例如:在b , m两相邻字母之间先添括号得到 , 再交换a , n的位置得到 , 下列说法:
A、 B、 C、 D、10. 学习添括号法则后,小明所在的学习小组为了加强对法则的理解,编了一个小游戏,游戏规则如下:把多项式看做a , , , , 五项的和,这五项可以依序循环站位,例如:当a站在第2位时,站在第一位,变为多项式 . 在任意相邻两个或三个字母左右添括号,再在符号不变的情况下,交换括号前后两字母的位置,则称此操作为“交换操作”,例如:在b , m两相邻字母之间先添括号得到 , 再交换a , n的位置得到 , 下列说法:①存在一种“交换操作”后的式子与原多项式一样;
②若每次操作只在相邻两个字母变换,则这样的变换共有5种不同的结果;
③存在两个变换后多项式的差只含两个字母。
其中正确的个数是( )
A、0 B、1 C、2 D、3二、填空题:(本大题8个小题,每小题4分,共32分)
-
11. 计算:。12. 有四张完全一样正面分别写有数字“-2”“3”“5”“7”的卡片,将其背面朝上并洗匀,从中随机抽取一张,记下卡片正面上的数字后放回,洗匀后再从中随机抽取一张,则抽取的两张卡片上的数字至少有一个是负数的概率是。13. 一个八边形的一个外角的度数是40°,则这个八边形的与这个角不相邻的7个内角的度数和为。14. 如图,在矩形ABCD中, , , 作AE平分∠BAD , 若连接BF , 则BF的长度为。
 15. “渝太太”“吖嘀吖嘀”等零售公司这几年在潼南迎来了蓬勃发展,其商品以价格亲民,品质较好,品种多样吸引了大量的顾客,今年4月份,潼南区江北一零售公司实现月纯利润为5万元,到6月份就突破到月纯利润为7.2万元,若该公司由4月份到6月份纯利润的月平均增长率为x , 根据题意,列出方程为。16. 在矩形ABCD中, , , 以A为圆心,AD为半径画弧交线段BC于E , 连接AE , 则阴影部分的面积为
15. “渝太太”“吖嘀吖嘀”等零售公司这几年在潼南迎来了蓬勃发展,其商品以价格亲民,品质较好,品种多样吸引了大量的顾客,今年4月份,潼南区江北一零售公司实现月纯利润为5万元,到6月份就突破到月纯利润为7.2万元,若该公司由4月份到6月份纯利润的月平均增长率为x , 根据题意,列出方程为。16. 在矩形ABCD中, , , 以A为圆心,AD为半径画弧交线段BC于E , 连接AE , 则阴影部分的面积为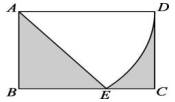 17. 若关于x的不等式组有且仅有四个整数解,关于y的分式方程有整数解,则符合条件的所有整数a的和是 .18. 对于任意一个三位自然数M , 若十位数字等于百位数字与个位数字的和减2,我们称这个三位数为“减2数”.例如:640,123.最大的“减2数”是 , 三位数是“减2数”,记 , , 若能被10整除,则满足条件的M的最大值是。
17. 若关于x的不等式组有且仅有四个整数解,关于y的分式方程有整数解,则符合条件的所有整数a的和是 .18. 对于任意一个三位自然数M , 若十位数字等于百位数字与个位数字的和减2,我们称这个三位数为“减2数”.例如:640,123.最大的“减2数”是 , 三位数是“减2数”,记 , , 若能被10整除,则满足条件的M的最大值是。三、解答题:(本大题共8个小题,19小题8分,20-26每小题10分)
-
19. 计算:(1)、(2)、20. 如图, , CB平分∠ABD .
 (1)、用尺规作图完成以下基本作图:作DE平分∠BDC , 分别交AB , BC于点E , O . 连接CE;(保留作图痕迹,不写作法和结论.)(2)、根据(1)中作图,证明四边形BDCE是菱形,请你补全证明过程.证明:∵ ,
(1)、用尺规作图完成以下基本作图:作DE平分∠BDC , 分别交AB , BC于点E , O . 连接CE;(保留作图痕迹,不写作法和结论.)(2)、根据(1)中作图,证明四边形BDCE是菱形,请你补全证明过程.证明:∵ ,∴ .
又∵CB平分∠ABD ,
∴① ▲ ,
∴ ,
∴② ▲ ,
同理:
∴③ ▲ ,
又∵即 ,
∴四边形BDCE是平行四边形.
∴四边形BDCE是菱形.(④ ).
21. 某校为了加强学生对防校园欺凌的认识,组织七、八年级全体学生进行了“防校园欺凌知识”竞赛,为了解竞赛成绩,现从该校七、八年级中各随机抽取10名学生的竞赛成绩(满分100分,90分及90分以上为优秀)进行整理、描述和分析(成绩得分用x表示,共分成四组:A. , B. , C. , D. , 下面给出了部分信息:七年级抽取的10名学生的竞赛成绩是:97,82,97,86,97,96,99,100,89,82
八年级抽取的10名学生的竞赛成绩在C组中的数据是:93,94,91
七、八年级抽取的学生竞赛成绩统计表:
年级
平均数
中位数
众数
七年级
92.5
96.5
c
八年级
92.5
b
100
八年级抽取的学生竞赛成绩扇形统计图:
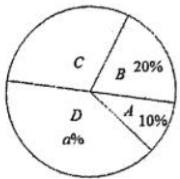
根据以上信息,解答下列问题:
(1)、图表中 , , ;(2)、根据以上数据,你认为该校七、八年级中哪个年级学生掌握防校园欺凌知识较好?请说明理由(一条理由即可);(3)、该校七年级有520人,八年级有460人参加了此次“防校园欺凌知识”竞赛,估计参加竞赛活动成绩优秀的学生人数是多少?22. 潼南的第一所大学---重庆电力高等专科学校第一批学生顺利入驻后,学校两旁自动形成的夜市生意也因此火爆起来,据调查,一饭店推出的两种炒饭受到了消费者的喜爱,其中“蛋炒饭”售价为15元/份,“肉丝炒饭”售价为20元/份,十月份平均每天可以卖出200份,总营业额3600元。(1)、求平均每天分别卖出多少份“蛋炒饭”和多少份“肉丝炒饭”?(2)、11月,饭店老板为回馈消费者,对两款炒饭价格进行了下调,“蛋炒饭”的售价比十月份的价格少3元,“肉丝炒饭”的售价比国庆期间的价格降低了10%,由此,11月的第一周里,“蛋炒饭”的销量比10月平均每天增加了3m份,“肉丝炒饭”的销量比国庆期间增加了5m%,最终这两款炒饭的总营业额比10月份平均每天的总营业额减少m%,请求出m的值.23. 如图1,△ABC是直角三角形, , , , 点P从点B出发,以每秒1个单位长度的速度沿着方向运动到A点停止,设 , 点P的运动时间为x秒。 (1)、直接写出y与x之间的函数表达式,并写出对应x的取值范围。(2)、在平面直角坐标系中画出y的图像,并写出y的一条性质(3)、结合作出的图像直接写出它与函数相交时x的值.(保留一位小数,误差不超过0.2)24. 如图,四边形ABCD是江北云海南湾小区外公园人工湖旁的林荫小道。晚饭后,小东陪爸爸妈妈散步,从A点出发,走了200米后到达B点,再走米后到达C点,再走一段路走到了D点,小东发现:B点在A点正西方向,C点在B点西北方向,在D点南偏西60°方向,D点恰好在点A的正北方。
(1)、直接写出y与x之间的函数表达式,并写出对应x的取值范围。(2)、在平面直角坐标系中画出y的图像,并写出y的一条性质(3)、结合作出的图像直接写出它与函数相交时x的值.(保留一位小数,误差不超过0.2)24. 如图,四边形ABCD是江北云海南湾小区外公园人工湖旁的林荫小道。晚饭后,小东陪爸爸妈妈散步,从A点出发,走了200米后到达B点,再走米后到达C点,再走一段路走到了D点,小东发现:B点在A点正西方向,C点在B点西北方向,在D点南偏西60°方向,D点恰好在点A的正北方。 (1)、求AD的长度。(2)、小东和小芳决定从B点同时出发来一场比赛,小东速度快,以5米每秒的平均速度沿的路线跑,小芳以4米每秒的平均速度沿的路线跑,谁先到达终点D?(参考数据:;)25. 如图,抛物线与x轴交于A、B两点,点A在点B的左边,与y轴交于点C , 点A、B的坐标为 ,
(1)、求AD的长度。(2)、小东和小芳决定从B点同时出发来一场比赛,小东速度快,以5米每秒的平均速度沿的路线跑,小芳以4米每秒的平均速度沿的路线跑,谁先到达终点D?(参考数据:;)25. 如图,抛物线与x轴交于A、B两点,点A在点B的左边,与y轴交于点C , 点A、B的坐标为 ,图1
 图2
图2 (1)、如图1,求抛物线的解析式;(2)、如图1,点D在直线BC上方的抛物线上运动(不含端点B、C),连接DC、DB , 当△BCD面积最大时,求出面积最大值和点D的坐标;(3)、如图2,将(1)中的抛物线向右平移,当它恰好经过原点时,设原抛物线与平移后的抛物线交于点E , 连接BE . 点M为原抛物线对称轴上一点,以B、E、M为顶点的三角形是直角三角形时,写出所有符合条件的点M的坐标,并写出求解点M的坐标的其中一种情况.26. 如图,在Rt△ABC中, , , 点E是CA延长线上一点,连接BE , 点D是AB边,上一动点,且 , 过点D作 , 垂足为点F .
(1)、如图1,求抛物线的解析式;(2)、如图1,点D在直线BC上方的抛物线上运动(不含端点B、C),连接DC、DB , 当△BCD面积最大时,求出面积最大值和点D的坐标;(3)、如图2,将(1)中的抛物线向右平移,当它恰好经过原点时,设原抛物线与平移后的抛物线交于点E , 连接BE . 点M为原抛物线对称轴上一点,以B、E、M为顶点的三角形是直角三角形时,写出所有符合条件的点M的坐标,并写出求解点M的坐标的其中一种情况.26. 如图,在Rt△ABC中, , , 点E是CA延长线上一点,连接BE , 点D是AB边,上一动点,且 , 过点D作 , 垂足为点F .图1
 图2
图2 图3
图3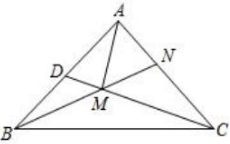 (1)、如图1,若 , , 求CF的长;(2)、如图2,连接AF , 求证:;(3)、如图3,过点A作 , 连接BM并延长交AC于点N , 若 , 当BM最小时,直接写出△ACM的面积.
(1)、如图1,若 , , 求CF的长;(2)、如图2,连接AF , 求证:;(3)、如图3,过点A作 , 连接BM并延长交AC于点N , 若 , 当BM最小时,直接写出△ACM的面积.