【培优卷】2024年浙教版数学八年级下册6.3 反比例函数的应用

试卷更新日期：2024-01-25 类型：同步测试

进入出卷网下载

一、选择题

1. 某品牌的饮水机接通电源就进入自动程序：开机加热到水温100℃，停止加热，水温开始下降，此时水温y(℃)与开机后用时.x(min)成反比例关系，直至水温降至30℃，饮水机关机.饮水机关机后即刻自动开机，重复上述自动程序.若在水温为30℃时，接通电源后，水温y(℃)和时间x(min)的关系如图所示，水温从100℃降到35℃所用的时间是（）

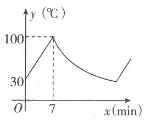A、27min B、20min C、13min D、7min

查看试题解析
2. 某种气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P(kPa)是气球体积V(m³)的反比例函数，其图象如图所示，当气球内的气压大于120 kPa时，气球将爆炸，为了安全，气球的体积应该（）

A、不夫于 $\frac{5}{4} m^{3}$ B、小于 $\frac{5}{4} m^{3}$ C、不小于 $\frac{4}{5} m^{3}$ D、小于 $\frac{4}{5} m^{3}$

查看试题解析
3. 某杠杆装置如图，杆的一端吊起一桶水，阻力臂保持不变在使杠杆平衡的情况下，小康通过改变动力臂L，测量出相应的动力F数据如表.请根据表中数据规律探求，当动力臂L长度为2.0m时，所需动力最接近（）
动力臂L（m）
动力F（N）
0.5
600
1.0
302
1.5
200
2.0
a
2.5
120

A、120N B、151N C、300N D、302N

查看试题解析
4. 某气球内充满了一定质量的气体，在温度不变的条件下，气球内气体的压强p(Pa)是气球体积V(m³)的反比例函数，且当V=1.5m³时，p=16000Pa，当气球内的气压大于40000Pa时，气球将爆炸，为确保气球不爆炸，气球的体积应(　　)

A、不小于0.5m³ B、不大于0.5m³ C、不小于0.6m³ D、不大于0.6m³

查看试题解析

二、填空题

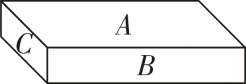
5. 如图，一块砖的 A，B，C三个面的面积之比是5：3： 1.若A，B，C三个面分别向下放在地上，地面所受压强分别为 P₁ ， P₂ ， P₃(压强的计算公式为 $p = \frac{F}{S} ，$ 其中p是压强，F是压力，S 是受力面积)，则 P₁ ， P₂ ， P₃的大小关系为(用“<”连接).

查看试题解析
6. 设矩形的一组邻边长分别为x，y，面积是 $S$ （S为定值），当 $x = 2$ 时，矩形的周长为6，则 $y$ 关于 $x$ 的函数表达式是，自变量 $x$ 的取值范围是.

查看试题解析
7. 小明要把一篇文章录入电脑，所需时间 $y (\min)$ 与录入文字的速度 $x$ （字 $/ \min$ ）之间的反比例函数关系如图所示，如果小明要在 $9 \min$ 内完成录入任务，则小明录入文字的速度至少为字 $/ \min$ .

查看试题解析
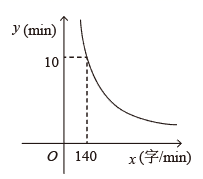8. 已知近视眼镜的度数D（度）与镜片焦距f（米）成反比例关系，且400度近视眼镜镜片的焦距为0.25米.小慧原来戴400度的近视眼镜，经过一段时间的矫正治疗后，现在只需戴镜片焦距为0.4米的眼镜了，则小慧所戴眼镜的度数降低了度.

查看试题解析
9. 为预防传染病，某校定期对教室进行“药熏消毒”，已知药物燃烧阶段，室内每立方米空气中的含药量y（mg）与燃烧时间x（分钟）成正比例；燃烧后，y与x成反比例（如图所示）．现测得药物10分钟燃烧完，此时教室内每立方米空气含药量为6mg．研究表明当每立方米空气中含药量低于1.2mg时，对人体方能无毒害作用，那么从消毒开始，至少需要经过分钟后，学生才能回到教室．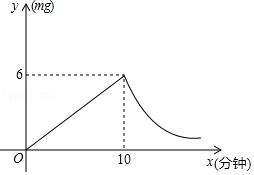

查看试题解析

三、综合题

10. 某小组进行漂洗实验，每次漂洗的衣服量和添加洗衣粉量固定不变实验发现，当每次漂洗用水量v（升）一定时，衣服中残留的洗衣粉量y（克）与漂洗次数x（次）满足y= $\frac{k v + 2.5}{x}$ （k为常数），已知当使用5升水，漂洗1次后，衣服中残留洗衣粉2克．

(1)、求k的值．

(2)、如果每次用水5升，要求漂洗后残留的洗衣粉量小于0.8克，求至少漂洗多少次？

(3)、现将20升水等分成x次（x>1）漂洗，要使残留的洗衣粉量降到0.5克，求每次漂洗用水多少升？

查看试题解析
11. 王老师驾驶小汽车从A地行驶到B地，行驶里程为480千米，设小汽车的行驶时间为t（单位：小时），行驶的平均速度为v（单位：千米/小时），且全程速度限定为不超过120千米/小时.

(1)、求v关于t的函数表达式；

(2)、王老师上午8点驾驶小汽车从A地出发.
①王老师需要在当天13点至14点（含13点和14点）间到达B地，求小汽车行驶的平均速度v需达到的范围；
②王老师能否在当天11点30分前到达B地？说明理由.

查看试题解析
12. 某市某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在温度为 $15^{°} C ~ 20^{°} C$ 的条件下生长最快的新品种，下图是某天恒温系统从开启到关闭及关闭后，大棚里温度 $y (^{°} C)$ 随时间x(h)变化的函数图象，其中AB段是恒温阶段，BC段是双曲线 $y = \frac{k}{x}$ 的一部分，请根据图中信息解答下列问题.

(1)、恒温系统在这天保持大棚内温度为 $20^{°} C$ 的时间有多少小时?

(2)、求 $k$ 的值.

(3)、恒温系统在一天24h内保持大棚温度在 $15^{°} C$ $~ 20^{°} C$ 的时间有多少小时?

查看试题解析
13. 某一农家计划利用已有的一堵长为8m的墙，用篱笆圈成一个面积为12m²的矩形ABCD花园，现在可用的篱笆总长为11m.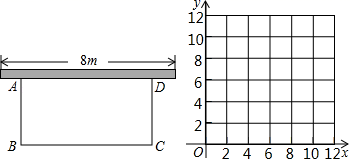

(1)、若设 $A B = x$ ， $B C = y$ .请写出y关于x的函数表达式；

(2)、若要使11m的篱笆全部用完，能否围成面积为15m²的花园？若能，请求出长和宽；若不能，请说明理由；

(3)、若要使11m的篱笆全部用完，请写出y关于x的第二种函数解析式.请在坐标系中画出两个函数的图象，观察图象，满足条件的围法有几种？请说明理由.

查看试题解析
14. 小华设计了一个探索杠杆平衡条件的实验：如图①，在一根匀质的木杆的中点 $O$ 左侧固定位置 $B$ 处悬挂重物 $A$ ，在中点 $O$ 的右侧用一个弹簧测力计向下拉木杆，改变弹簧测力计与点 $O$ 的距离 $x$ （单位： $c m$ ），观察弹簧测力计的示数 $y$ （单位： $N$ ）的变化情况，实验数据记录如下：
$x (c m)$
…
10
15
20
25
30
…
$y (N)$
…
30
20
15
12
10
…

(1)、把上表中 $(x, y)$ 的各组对应值作为点的坐标，在图②所示的直角坐标系中描出相应的点，用平滑曲线连结这些点，并观察所得的图象．猜测 $y$ 与 $x$ 之间的函数关系，并求出函数关系式．

(2)、当弹簧测力计的示数为 $24 N$ 时，弹簧测力计与点 $O$ 的距离是多少厘米？随着弹簧测力计与点 $O$ 的距离不断减小，弹簧测力计的示数将发生怎样的变化？

查看试题解析

动力臂L（m）	动力F（N）
0.5	600
1.0	302
1.5	200
2.0	a
2.5	120

$x (c m)$	…	10	15	20	25	30	…
$y (N)$	…	30	20	15	12	10	…