【基础卷】2024年浙教版数学八年级下册6.3 反比例函数的应用

试卷更新日期：2024-01-25 类型：同步测试

进入出卷网下载

一、选择题

1. 某工厂现有原材料100吨，每天平均用去x吨，这批原材料能用y天，则y与x之间的函数表达式为（）

A、 $y = 100 x$ B、 $y = \frac{100}{x}$ C、 $y = \frac{x}{2} + 100$ D、 $y = 100 - x$

查看试题解析
2. 近视眼镜的度数y(度)与镜片焦距x(m)成反比例.已知 400 度近视眼镜镜片的焦距为0.25 m，则y关于x的函数表达式为（）

A、 $y = \frac{400}{x}$ B、 $y = \frac{1}{4 x}$ C、 $y = \frac{100}{x}$ D、 $y = \frac{1}{400 x}$

查看试题解析
3. 已知经过闭合电路的电流 I(A)与电路的电阻R(Ω)是反比例函数关系，根据下表判断 a和b的大小关系为（）
I(A) 5 … a … … … b … 1
R(Ω) 20 30 40 50 60 70 80 90 100

A、a>b B、a≥b C、a<b D、a≤b

查看试题解析
4. 已知电灯电路两端的电压U为220 V，通过灯泡的电流强度 I(A)的最大限度为 0.11 A.设选用灯泡的电阻为 R(Ω)，则下列说法正确的是（）

A、R 至少 2 000 Ω B、R 至多 2000 Ω C、R 至少 24.2 Ω D、R 至多24.2Ω

查看试题解析
5. 公元前3世纪，古希腊科学家阿基米德发现了杠杆平衡，后来人们把它归纳为“杠杆原理”，即：阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头，已知阻力和阻力臂分别是1200N和0.5m，则动力F(单位：N)关于动力臂l(单位：m)的函数表达式正确的是（）

A、 $F = \frac{1200}{l}$ B、 $F = \frac{600}{l}$ C、 $F = \frac{500}{l}$ D、 $F = \frac{0.5}{l}$

查看试题解析
6. 某电子商城推出分期付款购买电脑的活动，一台电脑的售价为1.2万元，前期付款4000元，后期每个月分期付一定的数额，则每个月的付款额 $y$ (元)与付款月数 $x$ 之间的函数关系式是（）

A、 $y = \frac{8000}{x}$ （x为正整数) B、 $y = \frac{8}{x}$ C、 $y = \frac{8000}{x}$ D、 $y = 8000 x$

查看试题解析
7. 已知蓄电池的电压为定值，使用蓄电池时，电流I(A)与电阻 R(Ω)是反比例函数关系，它的图象如图所示.如果以此蓄电池为电源的用电器的限制电流为不能超过6 A，那么用电器的可变电阻R 应控制在（）

A、R≥2Ω B、0Ω<R≤2Ω C、R≥1Ω D、0Ω<R≤1Ω

查看试题解析

二、填空题

8. 在电压 $U$ 、电流 $I$ 、电阻 $R$ 中，当一定时，其余两个量成反比例.

查看试题解析
9. 近视眼镜的度数y（度）与镜片焦距x（m）成反比例，已知400度近视眼镜镜片的焦距为0.25m，则眼镜度数与镜片焦距之间的函数关系式为.

查看试题解析
10. 如图所示蓄电池的电压为定值，使用该蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示，如果以此蓄电池为电源的电器的限制电流不超过12A，那么用电器可变电阻R应控制的范围是．

查看试题解析
11. 近视眼镜的度数y（度）与镜片焦距x（米）成反比例，已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数y与镜片焦距x之间的函数关系式为.

查看试题解析

三、综合题

12. 设面积为 $12 c m^{2}$ 的平行四边形的一边长为 $a (c m)$ ，这条边上的高线长为 $h (c m)$ ．

(1)、求 $h$ 关于 $a$ 的函数表达式和自变量 $a$ 的取值范围．

(2)、当边长 $a = 6 c m$ 时，求这条边上的高线长．

查看试题解析
13. 在长方形硬纸片的四个角上都剪去一个边长为 $x (c m)$ 的正方形（如图所示的阴影部分），将其折成一个容积 $V = 600 c m^{3}$ 的无盖长方体形盒子．设长方体的底面积是 $S (c m^{2})$ ．

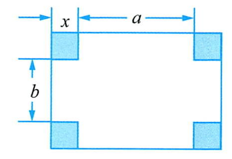(1)、求 $S$ 关于 $x$ 的函数表达式．

(2)、若 $S = 300 c m^{2}$ ，求长方体底面一边长 $a$ 关于底面另一边长 $b$ 的函数表达式．

查看试题解析
14. 已知小聪家与学校相距3000米，他从家里出发骑自行车去学校，设速度为 $v$ （米/分），到达学校所用的时间为 $t$ （分）．

(1)、求 $v$ 关于 $t$ 的函数表达式．这个函数是反比例函数吗？如果是，说出比例系数．

(2)、求当 $v = 200$ 时自变量 $t$ 的值，并说明这个值的实际意义．

(3)、利用 $v$ 关于 $t$ 的函数表达式说明：若小聪到达学校所用的时间减少到原来的 $\frac{5}{6}$ ，则他骑车的速度应怎样变化？

查看试题解析
15. 在探究欧姆定律时，小明发现小灯泡电路上的电压保持不变，通过小灯泡的电流越大，灯就越亮。设选用小灯泡的电阻为 R(Ω)，通过的电流强度为I(A)(欧姆定律公式： $I = \frac{U}{R} .$ ）

(1)、若电阻为40 Ω，通过的电流强度为0.30 A，求Ⅰ关于R的函数表达式.

(2)、如果电阻小于 40 Ω，那么与(1)中相比，小灯泡的亮度将发生怎样的变化?请说明理由.

查看试题解析

I(A)	5	…	a	…	…	…	b	…	1
R(Ω)	20	30	40	50	60	70	80	90	100