【基础卷】2024年浙教版数学八年级下册6.2 反比例函数的图象和性质
试卷更新日期:2024-01-24 类型:同步测试
一、选择题
-
1. 在同一坐标系中,函数y=和y=kx−2的图象大致是( )A、
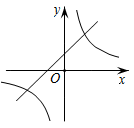 B、
B、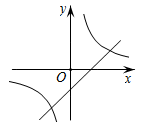 C、
C、 D、
D、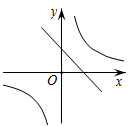 2. 已知矩形的长为 , 宽为 , 面积为 , 则与之间的函数关系用图象表示大致是( )A、
2. 已知矩形的长为 , 宽为 , 面积为 , 则与之间的函数关系用图象表示大致是( )A、 B、
B、 C、
C、 D、
D、 3. 已知A(1,y1),B(2,y2)两点在双曲线y上,且y1>y2 , 则m的取值范围是( )A、m<0 B、m>0 C、m D、m4. 若、都在函数的图象上,且 , 则( )A、 B、 C、 D、5. 已知点 , 都在反比例函数的图象上,且 , 则 , 的大小关系是( )A、 B、 C、 D、6. 如图,已知双曲线 经过矩形 边 的中点 且交 于 , 四边形 的面积为 2,则
3. 已知A(1,y1),B(2,y2)两点在双曲线y上,且y1>y2 , 则m的取值范围是( )A、m<0 B、m>0 C、m D、m4. 若、都在函数的图象上,且 , 则( )A、 B、 C、 D、5. 已知点 , 都在反比例函数的图象上,且 , 则 , 的大小关系是( )A、 B、 C、 D、6. 如图,已知双曲线 经过矩形 边 的中点 且交 于 , 四边形 的面积为 2,则 A、1 B、2 C、4 D、87. 如图,点A在反比例函数的图象上,轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为3,则k的值为( )
A、1 B、2 C、4 D、87. 如图,点A在反比例函数的图象上,轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为3,则k的值为( )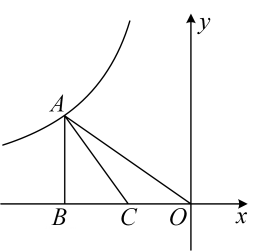 A、12 B、 C、6 D、8. 在平面直角坐标系中,反比例函数的图象经过点 , 则它的图象也一定经过的点是( )A、 B、 C、 D、
A、12 B、 C、6 D、8. 在平面直角坐标系中,反比例函数的图象经过点 , 则它的图象也一定经过的点是( )A、 B、 C、 D、二、填空题
-
9. 反比例函数y= 的图象在第象限.10. 反比例函数的图象分布在第一、三象限内,则的取值范围为 .11. 反比例函数的图象经过点 , 那么图像分布在象限.12. 如图,点A是反比例函数y= (x>0)上的一点,过点A作AC⊥y轴,垂足为点C,AC交反比例函数y=的图象于点B,点P是x轴上的动点,则△PAB的面积为 .
 13. 已知y与x成反比例,且当时, , 则当时,x的值为 .14. 某反比例函数的图象过点(-1,6),则该反比例函数的解析式为.15. 已知y与x成反比例,且当x=-3时,y=4,则当x=6时,y的值为.16. 若点 , 在同一个反比例函数的图象上,则 的值为.17. 若点在反比例函数的图象上,则代数式的值为 .
13. 已知y与x成反比例,且当时, , 则当时,x的值为 .14. 某反比例函数的图象过点(-1,6),则该反比例函数的解析式为.15. 已知y与x成反比例,且当x=-3时,y=4,则当x=6时,y的值为.16. 若点 , 在同一个反比例函数的图象上,则 的值为.17. 若点在反比例函数的图象上,则代数式的值为 .三、解答题
-
18. 如图,在平面直角坐标系中,△OAC的边OC 在y轴正半轴上,反比例函数(k>0,x>0)的图象经过点 A 和 B(2,6),且 B为AC 的中点。求:
 (1)、k的值和点C 的坐标.(2)、△OAB的面积.
(1)、k的值和点C 的坐标.(2)、△OAB的面积.