广西壮族自治区河池市凤山县2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-01-24 类型：期末考试

进入出卷网下载

一、选择题（共12小题，每小题3分，共36分.在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑.）

1. 先贤孔子曾说过“鼓之舞之”，这是“鼓舞”一词最早的起源，如图是喜庆集会时击鼓瞬间的情景及鼓的立体图形，该立体图形的主视图是（）

A、 B、 C、 D、

查看试题解析
2. 从数学的观点看，对以下成语及诗句中的事件判断正确的是（）

A、成语“守株待兔”是随机事件 B、成语“水中捞月”是随机事件 C、诗句“清明时节雨纷纷”是必然事件 D、诗句“离离原上草，一岁一枯荣”是不可能事件

查看试题解析
3. 中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录，下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大雪”，其中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 在Rt△ABC中，各边都扩大5倍，则∠A的三角函数值（）

A、不变 B、扩大5倍 C、缩小5倍 D、不能确定

查看试题解析
5. 函数 $y = a x + 1$ 与 $y = a x^{2} + b x + 1$ （a ， b是常数，且 $a \neq 0$ ）在同一坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
6. 如图，PA、PB是 $⊙ O$ 的切线，切点分别为A、B ，点C在 $\overset{⌢}{A B}$ 上，过点C的切线分别交PA、PB于点D、E ，若 $P A = 1$ ，则 $△ P D E$ 的周长为（）

A、 $\sqrt{3}$ B、2 C、3 D、6

查看试题解析
7. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，下列说法错误的是（）

A、图象关于直线 $x = 1$ 对称 B、函数 $y = a x^{2} + b x + c (a \neq 0)$ 的最小值是－4 C、当 $x < 1$ 时，y随x的增大而增大 D、－1和3是方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个根

查看试题解析
8. 如图是反比例函数 $y_{1} = \frac{2}{x}$ 和 $y_{2} = - \frac{4}{x}$ 在x轴上方的图象，x轴的平行线AB分别与这两个函数图象交于A、B两点，点 $P (- 5.5 ， 0)$ 在x轴上，则 $△ P A B$ 的面积为（）

A、3 B、6 C、8.2 D、16.5

查看试题解析
9. 对于实数a ， b定义运算“※”为 $a \times b = a + b^{2}$ ，例如 $3 ※ 2 = 3 + 2^{2} = 7$ ，则关于x的方程 $x ※ (x + 1) = 5$ 的解是（）

A、 $x = - 4$ B、 $x = - 1$ C、 $x_{1} = - 1$ ， $x_{2} = 4$ D、 $x_{1} = 1$ ， $x_{2} = - 4$

查看试题解析
10. 如图，已知 $△ A B C$ 是一块锐角三角形材料，边 $B C = 120 m m$ ，高 $A D = 80 m m$ ，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB ， AC上，这个正方形零件的边长是（）

A、48mm B、80mm C、20mm D、46mm

查看试题解析
11. 《四元玉鉴》是一部成就辉煌的数学名著，是宋元数学集大成者，也是我国古代水平最高的一部数学著作.该著作记载了“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽.每株脚钱三文足，无钱准与一株椽”.大意是：现请人代买一批椽，这批椽的总售价为6210文.如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设6210元购买椽的数量为x株，则符合题意的方程是（）

A、 $\frac{6210}{x} = 3 x$ B、 $3 (x - 1) = 6210$ C、 $3 (x - 1) = \frac{6210}{x}$ D、 $3 (x - 1) = \frac{6210}{x - 1}$

查看试题解析
12. 如图，已知 $△ A B C$ 的三个顶点均在正方形格点上，则下列结论错误的为（）

A、 $c o s C = \frac{\sqrt{5}}{5}$ B、 $t a n B \cdot t a n C = 1$ C、 $t a n B = \frac{1}{2}$ D、 $s i n B = \sqrt{5}$

查看试题解析

二、填空题（本大题共6小题，每小题2分，共12分.）

13. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = 5$ ， $A C = 12$ ，则 $t a n A$ 的值是.

查看试题解析
14. 某射击运动员在同一条件下的射击成绩记录如下：
射击次数
20
80
100
200
400
1000
“射中8环以上”的次数
18
68
82
168
327
823
“射中8环以上”的频率（结果保留两位小数）
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性，估计这名运动员射击一次时“射中8环以上”的概率约是.

查看试题解析
15. 如图，粮仓的顶部是圆锥形状，这个圆锥的底面圆的半径为3米，母线长为6米，为防雨水，需要在粮仓顶部铺上油毡，如果油毡的市场价为10元/米，那么购买油毡所需要的费用是元.（结果保留 $π$ ）

查看试题解析
16. 美是一种感觉，当人体下半身长与身高的比值越接近0.618时，越给人一种美感.已知某女士的身高为160cm，下半身长x与身高l的比值是0.60，为尽可能达到好的效果，她应穿的高跟鞋的高度大约为.（精确到0.1cm）

查看试题解析
17. 如图是某种型号的飞机，飞机着陆后滑行的距离s（单位：m），关于滑行时间t（单位：s）的函数解析式是 $s = 100 t - 2.5 t^{2}$ ，则此型号飞机着陆后滑行m停下来.

查看试题解析
18. 如图，△AOB是直角三角形，∠AOB=90°，∠ABO=30°，点A在反比例函数y= $\frac{2}{x}$ 的图象上，若点B在反比例函数y= $\frac{k}{x}$ 的图象上，则k= ．

查看试题解析

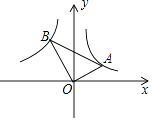
三、解答题（本大题共8小题，共72分.解答应写出文字说明、证明过程或演算步骤.）

19. 计算： $- 16 \div {(- 2)}^{3} - 2^{2} \times | - \frac{1}{2} | + {(- 1)}^{2023}$

查看试题解析
20. 先化简，再求值： $\frac{x^{2} - x}{x^{2} + 2 x + 1} \div (\frac{2}{x + 1} - \frac{1}{x})$ ，化简后，从 $- 2 < x < 3$ 的范围内选择一个你喜欢的整数作为x的值代入求值.

查看试题解析
21. 如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度；已知 $△ A B C$ .

(1)、作出 $△ A B C$ 以O为旋转中心，顺时针旋转 $90 °$ 的 $△ A_{1} B_{1} C_{1}$ （只画出图形）.

(2)、作出 $△ A B C$ 关于原点O成中对心称的 $△ A_{2} B_{2} C_{2}$ ，（只画出图形）；

(3)、请在y轴上找一点P ，使 $P B_{1} + P C_{1}$ 的值最小，并直接写出点P的坐标.

查看试题解析
22. （本题满分10分）某校在课后服务中，成立了以下社团：A.计算机，B.围棋，C.篮球，D.书法.每人只能加入一个社团，为了解学生参加社团的情况，从参加社团的学生中随机抽取了部分学生进行调查，并将调查结果绘制成如下两幅不完整的统计图，其中图1中D所占扇形的圆心角为 $150 °$ .
图1 图2
请结合图中所给信息解答下列问题：

(1)、这次被调查的学生共有人；

(2)、请你将条形统计图补充完整；

(3)、若该校共有1800学生加入了社团，请你估计这1800名学生中有多少人参加了篮球社团；

(4)、在书法社团活动中，由于甲、乙、丙、丁四人平时的表现优秀，恰好四位同学中有两名是男同学，两名是女同学.现决定从这四人中任选两名参加全市书法大赛，用画树状图求恰好选中一男一女的概率.

查看试题解析
23. 【学科融合】如图1，在反射现象中，反射光线，入射光线和法线都在同一个平面内；反射光线和入射光线分别位于法线两侧；反射角r等于入射角i.这就是光的反射定律.
【问题解决】如图2.小红同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙、木板和平面镜，手电筒的灯泡在点G处，手电筒的光从平面镜上点B处反射后，恰好经过木板的边缘点F ，落在墙上的点E处，点E到地面的高度 $D E = 3.5 m$ ，点F到地面的高度 $C F = 1.5 m$ ，灯泡到木板的水平距离 $A C = 5.4 m$ ，木板到墙的水平距离为 $C D = 4 m$ .图中点A ， B ， C ， D在同一条直线上.
图1 图2

(1)、求BC的长；

(2)、求灯泡到地面的高度AG.

查看试题解析
24. 我校的饮水机接通电源就进入自动程序，开机加热时每分钟上升 $10 ° C$ ，加热到 $100 ° C$ ，停止加热，水温开始下降，此时水温（ $° C$ ）与开机后用时（min）成反比例关系.直至水温降至 $20 ° C$ 时自动开机加热，重复上述自动程序.若在水温为 $20 ° C$ 时，接通电源后，水温 $y (° C)$ 和时间x（min）的关系如图所示.

(1)、 $a =$ ， $b =$ .

(2)、直接写出图中y关于x的函数表达式.

(3)、饮水机有多少时间能使水温保持在 $50 ° C$ 及以上？

(4)、若某天上午7：00饮水机自动接通电源，开机温度正好是 $20 ° C$ ，问学生上午第一节下课时（8：40）能喝到 $50 ° C$ 以上的水吗？请说明理由.

查看试题解析
25. 如图，AB是 $⊙ O$ 的直径， $C D = C B$ ， $C E ⊥ A B$ 于点E ，连接BD交CE于点F.

(1)、求证： $C F = B F$ .

(2)、若 $C D = 4 \sqrt{5}$ ， $A C = 8 \sqrt{5}$ ，求弦BD的长.

查看试题解析
26. 某智能机器人生产厂家准备对甲、乙两款机器人进行投资生产，根据前期市场调研情况发现，投资甲机器人一年后的收益 $y_{甲}$ （万元）与投入成本x（ $x > 0$ ）（万元）的函数表达式为： $y_{甲} = \frac{1}{2} x$ ，投资乙机器人一年后的收益 $y_{乙}$ （万元）与投入成本x（ $x > 0$ ）（万元）的函数表达式为： $y_{乙} = - \frac{1}{4} x^{2} + \frac{5}{2} x$ .

(1)、若将2万元资金投给乙机器人，一年后获得的收益是多少？

(2)、请在平面直角坐标系中画出两函数图象的简图，并结合图象分析怎样选择投资对象使获得的收益更多？

(3)、若该生产厂家共有活动资金32万元，计划全部投入到甲、乙两款机器人生产中，当甲、乙两款机器人分别投入多少万元时，一年后获得的收益之和最大？最大值是多少万元？

查看试题解析

射击次数	20	80	100	200	400	1000
“射中8环以上”的次数	18	68	82	168	327	823
“射中8环以上”的频率（结果保留两位小数）	0.90	0.85	0.82	0.84	0.82	0.82